2.1合情推理(1)
图片预览








文档简介
课件38张PPT。已知的判断新的判断 根据一个或几个已知的判断来确定一个新的判断的思维过程就叫推理.推理与证明推理证明言之有理,论证有据!第二章 推理与证明丽水中学 瞿晓军2.1.1合情推理(1)10= 3+7
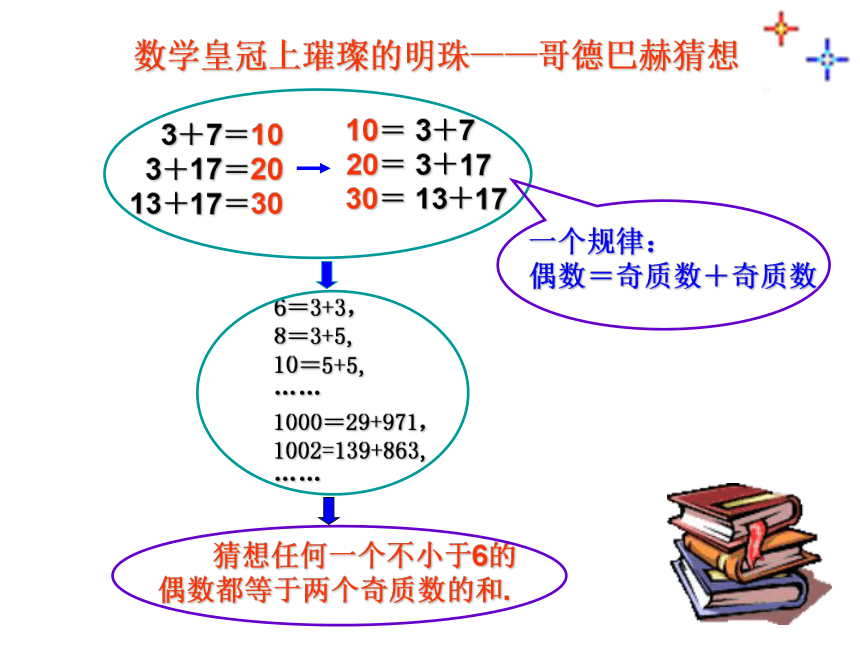
20= 3+17
30= 13+17数学皇冠上璀璨的明珠——哥德巴赫猜想哥德巴赫猜想的过程:归纳推理的过程: 由某类事物的 具有某些特征,
推出该类事物的 都具有这些特征
的推理,或者由 概括出
的推理,称为归纳推理(简称归纳).部分对象全部对象个别事实一般结论归纳推理 1,3,5,7,…,由此你猜想出第
个数是_______.这就是从部分到整体,从个别到一般的归纳推理.你想起来了吗?成语“一叶知秋”统计初步中的用样本估计总体 通过从总体中抽取部分对象进
行观测或试验,进而对整体做出推断. 意思是从一片树叶的凋落,知道秋
天将要来到.比喻由细微的迹象看出整体
形势的变化,由部分推知全体. 1.已知数列{ }的第一项 =1,
且 ( =1,2,3,···),
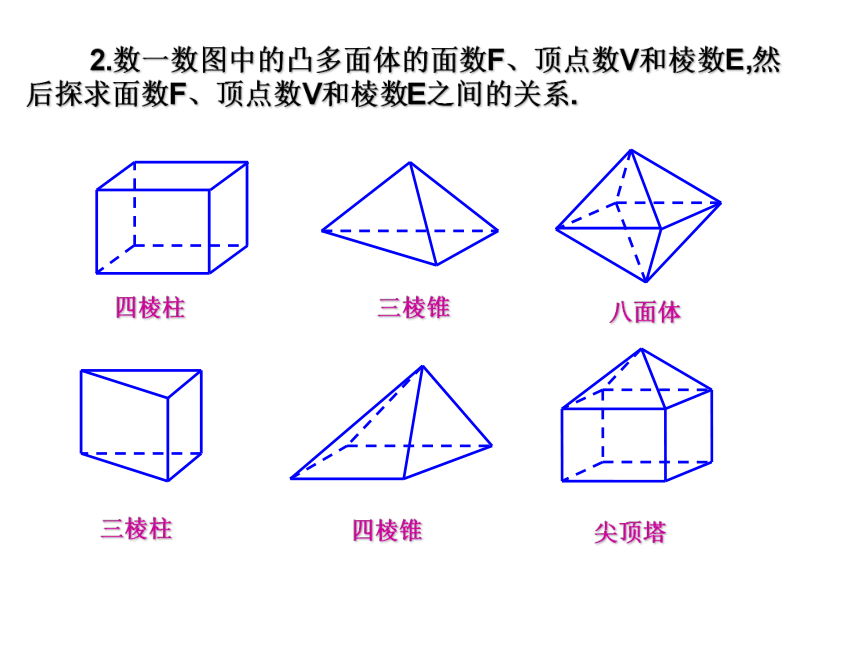
请归纳出这个数列的通项公式为________.让我们一起来归纳推理 2.数一数图中的凸多面体的面数F、顶点数V和棱数E,然后探求面数F、顶点数V和棱数E之间的关系.四棱柱三棱锥八面体三棱柱四棱锥尖顶塔四棱柱6812四棱柱6812644三棱锥四棱柱6812644三棱锥1286八面体四棱柱6812644三棱锥1286八面体695三棱柱四棱柱6812644三棱锥1286八面体695三棱柱558四棱锥四棱柱6812644三棱锥1286八面体695三棱柱558四棱锥9169尖顶塔695955816968126441286猜想凸多面体的面数F、顶点数V和棱数E之间的关系式为:F+V-E=2欧拉公式归纳推理的基础归纳推理的作用归纳推理观察、分析发现新事实、获得新结论由部分到整体、
个别到一般的推理注意归纳推理的结论不一定成立可能有生命存在有生命存在温度适合生物的生存一年中有四季的变更有大气层行星、围绕太阳运行、绕轴自转火星地球火星上是否存在生命火星与地球类比的思维过程:火星地球存在类似特征 由两类对象具有某些类似特征和其中
一类对象的某些已知特征,推出另一类对
象也具有这些特征的推理称为类比推理.类比推理我们已经学习过“等差数列”与“等比数列”.你是否想过“等和数列”、“等积数列” ? 从第二项起,每一项与其前一项的差等于一个常数的数列是等差数列. 从第二项起,每一项与其前一项的和等于一个常数的数列是等和数列.试根据等式的性质猜想不等式的性质.类比推理的结论不一定成立.让我们一起来类比推理探究球心与截面圆(不经过球心的截面圆)
圆心连线垂直于截面圆.与球心距离相等的两截面圆面积相等;与球心距离不等的两截面圆面积不等,距球心较近的截面圆面积较大.以点P(x0,y0,z0)为球心,r为半径的球的方程为
(x-x0)2+(y-y0)2+(z-z0)2=r2.类比推理类比推理
以旧的知识为基础,推测新的结果,具有发现的功能
由特殊到特殊的推理类比推理的结论不一定成立注意类比推理由特殊到特殊的推理;以旧的知识为基础,推测新的结果;结论不一定成立.归纳推理由部分到整体、特殊到一般的推理;以观察分析为基础,推测新的结论;具有发现的功能;结论不一定成立.具有发现的功能;归纳推理和类比推理的过程通俗地说,合情推理是指“合乎情理”的推理. 传说在古老的印度有一座神庙,神庙中有三根针和套在一根针上的64个圆环.古印度的天神指示他的僧侣们按下列规则,把圆环从一根针上全部移到另一根针上,第三根针起“过渡”的作用.
1.每次只能移动1个圆环;
2.较大的圆环不能放在较小的圆环上面.
如果有一天,僧侣们将这64个圆环全部移到另一根针上,那么世界末日就来临了.
请你试着推测:把 个圆环从1号针移到3号针,最少需要移动多少次?123游戏:河内塔(Tower of Hanoi)123第1个圆环从1到3.设 为把 个圆环从1号针移到3号针的最少次数,则 =1时, =1 =2时,123第1个圆环从1到3.前1个圆环从1到2;
第2个圆环从1到3;
第1个圆环从2到3.设 为把 个圆环从1号针移到3号针的最少次数,则 =1 =1时, =3 =2时, =3 =1时, =1 =3时,123第1个圆环从1到3.前1个圆环从1到2;
第2个圆环从1到3;
前1个圆环从2到3.前2个圆环从1到2;
第3个圆环从1到3;
前2个圆环从2到3.设 为把 个圆环从1号针移到3号针的最少次数,则 =71.课本习题2.1A组1,3,5;
2.找一个你感兴趣的数学定义、公式或定理,探究它的来源,你也可以通过翻阅书籍、上网查找资料来寻求依据.作业善于观察勤于思考敢于猜想的人常常会冒出创造的灵感火花再 见
20= 3+17
30= 13+17数学皇冠上璀璨的明珠——哥德巴赫猜想哥德巴赫猜想的过程:归纳推理的过程: 由某类事物的 具有某些特征,
推出该类事物的 都具有这些特征
的推理,或者由 概括出
的推理,称为归纳推理(简称归纳).部分对象全部对象个别事实一般结论归纳推理 1,3,5,7,…,由此你猜想出第
个数是_______.这就是从部分到整体,从个别到一般的归纳推理.你想起来了吗?成语“一叶知秋”统计初步中的用样本估计总体 通过从总体中抽取部分对象进
行观测或试验,进而对整体做出推断. 意思是从一片树叶的凋落,知道秋
天将要来到.比喻由细微的迹象看出整体
形势的变化,由部分推知全体. 1.已知数列{ }的第一项 =1,
且 ( =1,2,3,···),
请归纳出这个数列的通项公式为________.让我们一起来归纳推理 2.数一数图中的凸多面体的面数F、顶点数V和棱数E,然后探求面数F、顶点数V和棱数E之间的关系.四棱柱三棱锥八面体三棱柱四棱锥尖顶塔四棱柱6812四棱柱6812644三棱锥四棱柱6812644三棱锥1286八面体四棱柱6812644三棱锥1286八面体695三棱柱四棱柱6812644三棱锥1286八面体695三棱柱558四棱锥四棱柱6812644三棱锥1286八面体695三棱柱558四棱锥9169尖顶塔695955816968126441286猜想凸多面体的面数F、顶点数V和棱数E之间的关系式为:F+V-E=2欧拉公式归纳推理的基础归纳推理的作用归纳推理观察、分析发现新事实、获得新结论由部分到整体、
个别到一般的推理注意归纳推理的结论不一定成立可能有生命存在有生命存在温度适合生物的生存一年中有四季的变更有大气层行星、围绕太阳运行、绕轴自转火星地球火星上是否存在生命火星与地球类比的思维过程:火星地球存在类似特征 由两类对象具有某些类似特征和其中
一类对象的某些已知特征,推出另一类对
象也具有这些特征的推理称为类比推理.类比推理我们已经学习过“等差数列”与“等比数列”.你是否想过“等和数列”、“等积数列” ? 从第二项起,每一项与其前一项的差等于一个常数的数列是等差数列. 从第二项起,每一项与其前一项的和等于一个常数的数列是等和数列.试根据等式的性质猜想不等式的性质.类比推理的结论不一定成立.让我们一起来类比推理探究球心与截面圆(不经过球心的截面圆)
圆心连线垂直于截面圆.与球心距离相等的两截面圆面积相等;与球心距离不等的两截面圆面积不等,距球心较近的截面圆面积较大.以点P(x0,y0,z0)为球心,r为半径的球的方程为
(x-x0)2+(y-y0)2+(z-z0)2=r2.类比推理类比推理
以旧的知识为基础,推测新的结果,具有发现的功能
由特殊到特殊的推理类比推理的结论不一定成立注意类比推理由特殊到特殊的推理;以旧的知识为基础,推测新的结果;结论不一定成立.归纳推理由部分到整体、特殊到一般的推理;以观察分析为基础,推测新的结论;具有发现的功能;结论不一定成立.具有发现的功能;归纳推理和类比推理的过程通俗地说,合情推理是指“合乎情理”的推理. 传说在古老的印度有一座神庙,神庙中有三根针和套在一根针上的64个圆环.古印度的天神指示他的僧侣们按下列规则,把圆环从一根针上全部移到另一根针上,第三根针起“过渡”的作用.
1.每次只能移动1个圆环;
2.较大的圆环不能放在较小的圆环上面.
如果有一天,僧侣们将这64个圆环全部移到另一根针上,那么世界末日就来临了.
请你试着推测:把 个圆环从1号针移到3号针,最少需要移动多少次?123游戏:河内塔(Tower of Hanoi)123第1个圆环从1到3.设 为把 个圆环从1号针移到3号针的最少次数,则 =1时, =1 =2时,123第1个圆环从1到3.前1个圆环从1到2;
第2个圆环从1到3;
第1个圆环从2到3.设 为把 个圆环从1号针移到3号针的最少次数,则 =1 =1时, =3 =2时, =3 =1时, =1 =3时,123第1个圆环从1到3.前1个圆环从1到2;
第2个圆环从1到3;
前1个圆环从2到3.前2个圆环从1到2;
第3个圆环从1到3;
前2个圆环从2到3.设 为把 个圆环从1号针移到3号针的最少次数,则 =71.课本习题2.1A组1,3,5;
2.找一个你感兴趣的数学定义、公式或定理,探究它的来源,你也可以通过翻阅书籍、上网查找资料来寻求依据.作业善于观察勤于思考敢于猜想的人常常会冒出创造的灵感火花再 见
