11.3不等式的性质 课件(共17张PPT)2022-2023学年苏科版七年级数学下册
文档属性
| 名称 | 11.3不等式的性质 课件(共17张PPT)2022-2023学年苏科版七年级数学下册 |

|
|
| 格式 | pptx | ||
| 文件大小 | 1.2MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 苏科版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-09-12 14:34:58 | ||
图片预览






文档简介
(共17张PPT)
不等式的性质
学习目标:
(1)探索并理解不等式的性质.
(2)体会探索过程中所应用的归纳和类比的数学思想方法.
学习重点:
探索不等式的性质.
不 等 式 的 性 质
由a+2=b+2, 能得到a=b?
由0.5a=0.5b, 能得到a=b?
由 -2a= -2b, 能得到a=b?
由a-2=b-2, 能得到a=b?
复习回顾
复习回顾
一.等式的性质
等式的基本性质1:在等式两边都加上(或减去)同一个数或整式,结果仍相等.
如果a=b,那么a±c=b±c
等式的基本性质2:在等式两边都乘以或除以同一个数(除数不为0),结果仍相等.
如果a=b,那么ac=bc或 (c≠0),
【提出问题】
问题1
等式两边加上或减去同一个数(或整式),乘或除以同一个数(除数不为0),结果仍相等. 不等式是否也有类似的性质呢?
问题2
能用解方程的方法解不等式x+1 < 4
和- 2x > 6吗?
小明的年龄比小丽大.设今年小明a岁,小丽b岁,那么a b.
3年后小明的年龄比小丽 ,你能写出相应的不等式吗?3年前呢?n年后呢?n年前呢?请完成下表.
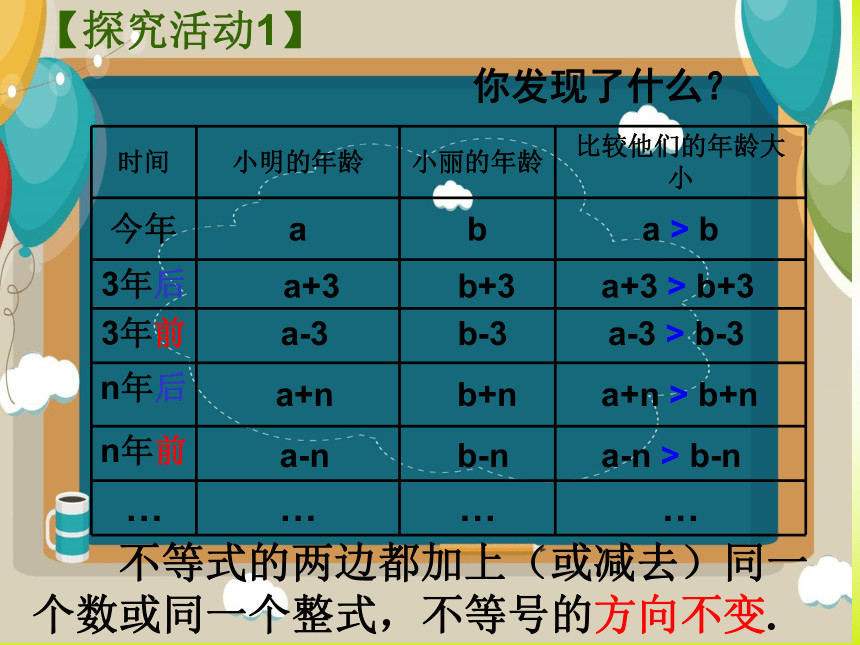
时间 小明的年龄 小丽的年龄 比较他们的年龄大小
今年 a b a > b
3年后
3年前
n年后
n年前
… … … …
不等式的两边都加上(或减去)同一个数或同一个整式,不等号的方向不变.
你发现了什么?
b+3
【探究活动1】
a+3
a+3 > b+3
a-3
b-3
a-3 > b-3
a+n
b+n
a+n > b+n
a-n
b-n
a-n > b-n
不等式的两边都加上(或减去)同一个数或同一个整式,不等号的方向不变.
如果 a >b
那么 a+c>b+c(或a-c>b-c)
不等式的性质1
(1)若a(2)若m>n,则m-(-h)___n-(-h)
不等式的两边都乘(或除以)同一个不为零的数,不等号的方向是不是也不变呢?
将不等式5>3两边分别乘同一个数,用不等号填空:
5×1 3×1,
5×2 3×2,
5×3 3×3,
5×4 3×4,
···
5×(-1) 3×(-1),
5×(-2) 3×(-2),
5×(-3) 3×(-3),
5×(-4) 3×(-4),
···
不等号的方向不改变.
不等号的方向改变了.
思考:不等式的两边都乘以0,结果又怎样?
结果变为恒等式,即0 = 0.
【探究活动2】
不等式的两边都乘(或除以)同一个正数,不等号的方向不变;
如果a>b,c<0 ,那么ac不等式的两边都乘(或除以)同一个负数,不等号的方向改变.
如果a>b,c>0 ,那么ac>bc,
不等式的性质2
(1)x-6<y-6 (2) 3x<3y
(3) -2x<-2y (4) x+9>y+9
(5) 2x+1>2y+1 (6)-3x-1>-3y-1
已知x >y,下列不等式一定成立吗?
练习:
在下列各题横线上填入不等号,使不等式成立.并说明是根据哪一条不等式基本性质.
(1)若a-3<9, 则 a ______12;
(2)若-a<10, 则 a______ -10;
(3)若 > -1, 则 a ______-4 ;
(4)若 > 0, 则 a _______ 0 ;
<
>
<
>
练习:
将下列不等式化成“x>a”或“x<a”的形式:
(1)x - 5>-1
(2)-2x>3
(3)2x- 1<2
(4)-6x <5
x>4
x<-1.5
x <1.5
x >-
练习:
已知a<b,用“<”或“>”号填空:
(1)a-3___b-3 (2) 6a____6b
(3) –a___-b (4) a-b____0
练习:
已知a<0,用“<”或“>”号填空:
(1)a+2 ______ 2; (2)a-1 ______ -1;
(3)3a______ 0; (4) ______0;
(5)a2_____0; (6)a3______0
(7)a-1______0; (8)|a|______0.
<
<
<
<
<
>
>
>
练习:
通过今天的学习,不等式有那些性质?根据不等式的性质,我们可以把不等式化为“x>a”或“x<a”的形式,通常有哪些步骤?
11.3 不等式的性质
不等式的性质
学习目标:
(1)探索并理解不等式的性质.
(2)体会探索过程中所应用的归纳和类比的数学思想方法.
学习重点:
探索不等式的性质.
不 等 式 的 性 质
由a+2=b+2, 能得到a=b?
由0.5a=0.5b, 能得到a=b?
由 -2a= -2b, 能得到a=b?
由a-2=b-2, 能得到a=b?
复习回顾
复习回顾
一.等式的性质
等式的基本性质1:在等式两边都加上(或减去)同一个数或整式,结果仍相等.
如果a=b,那么a±c=b±c
等式的基本性质2:在等式两边都乘以或除以同一个数(除数不为0),结果仍相等.
如果a=b,那么ac=bc或 (c≠0),
【提出问题】
问题1
等式两边加上或减去同一个数(或整式),乘或除以同一个数(除数不为0),结果仍相等. 不等式是否也有类似的性质呢?
问题2
能用解方程的方法解不等式x+1 < 4
和- 2x > 6吗?
小明的年龄比小丽大.设今年小明a岁,小丽b岁,那么a b.
3年后小明的年龄比小丽 ,你能写出相应的不等式吗?3年前呢?n年后呢?n年前呢?请完成下表.
时间 小明的年龄 小丽的年龄 比较他们的年龄大小
今年 a b a > b
3年后
3年前
n年后
n年前
… … … …
不等式的两边都加上(或减去)同一个数或同一个整式,不等号的方向不变.
你发现了什么?
b+3
【探究活动1】
a+3
a+3 > b+3
a-3
b-3
a-3 > b-3
a+n
b+n
a+n > b+n
a-n
b-n
a-n > b-n
不等式的两边都加上(或减去)同一个数或同一个整式,不等号的方向不变.
如果 a >b
那么 a+c>b+c(或a-c>b-c)
不等式的性质1
(1)若a(2)若m>n,则m-(-h)___n-(-h)
不等式的两边都乘(或除以)同一个不为零的数,不等号的方向是不是也不变呢?
将不等式5>3两边分别乘同一个数,用不等号填空:
5×1 3×1,
5×2 3×2,
5×3 3×3,
5×4 3×4,
···
5×(-1) 3×(-1),
5×(-2) 3×(-2),
5×(-3) 3×(-3),
5×(-4) 3×(-4),
···
不等号的方向不改变.
不等号的方向改变了.
思考:不等式的两边都乘以0,结果又怎样?
结果变为恒等式,即0 = 0.
【探究活动2】
不等式的两边都乘(或除以)同一个正数,不等号的方向不变;
如果a>b,c<0 ,那么ac
如果a>b,c>0 ,那么ac>bc,
不等式的性质2
(1)x-6<y-6 (2) 3x<3y
(3) -2x<-2y (4) x+9>y+9
(5) 2x+1>2y+1 (6)-3x-1>-3y-1
已知x >y,下列不等式一定成立吗?
练习:
在下列各题横线上填入不等号,使不等式成立.并说明是根据哪一条不等式基本性质.
(1)若a-3<9, 则 a ______12;
(2)若-a<10, 则 a______ -10;
(3)若 > -1, 则 a ______-4 ;
(4)若 > 0, 则 a _______ 0 ;
<
>
<
>
练习:
将下列不等式化成“x>a”或“x<a”的形式:
(1)x - 5>-1
(2)-2x>3
(3)2x- 1<2
(4)-6x <5
x>4
x<-1.5
x <1.5
x >-
练习:
已知a<b,用“<”或“>”号填空:
(1)a-3___b-3 (2) 6a____6b
(3) –a___-b (4) a-b____0
练习:
已知a<0,用“<”或“>”号填空:
(1)a+2 ______ 2; (2)a-1 ______ -1;
(3)3a______ 0; (4) ______0;
(5)a2_____0; (6)a3______0
(7)a-1______0; (8)|a|______0.
<
<
<
<
<
>
>
>
练习:
通过今天的学习,不等式有那些性质?根据不等式的性质,我们可以把不等式化为“x>a”或“x<a”的形式,通常有哪些步骤?
11.3 不等式的性质
同课章节目录
- 第7章 平面图形的认识(二)
- 7.1 探索直线平行的条件
- 7.2 探索平行线的性质
- 7.3 图形的平移
- 7.4 认识三角形
- 7.5 多边形的内角和与外角和
- 第8章 幂的运算
- 8.1 同底数幂的乘法
- 8.2 幂的乘方与积的乘方
- 8.3 同底数幂的除法
- 第9章 整式乘法与因式分解
- 9.1 单项式乘单项式
- 9.2 单项式乘多项式
- 9.3 多项式乘多项式
- 9.4 乘法公式
- 9.5 多项式的因式分解
- 第10章 二元一次方程组
- 10.1 二元一次方程
- 10.2 二元一次方程组
- 10.3 解二元一次方程组
- 10.4 三元一次方程组
- 10.5 用二元一次方程解决问题
- 第11章 一元一次不等式
- 11.1 生活中的不等式
- 11.2 不等式的解集
- 11.3 不等式的性质
- 11.4 解一元一次不等式
- 11.5 用一元一次不等式解决问题
- 11.6 一元一次不等式组
- 第12章 证明
- 12.1 定义与命题
- 12.2 证明
- 12.3 互逆命题
