13.3.1等腰三角形(第1课时) 课件(27张PPT)
文档属性
| 名称 | 13.3.1等腰三角形(第1课时) 课件(27张PPT) |

|
|
| 格式 | pptx | ||
| 文件大小 | 947.9KB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-09-12 09:10:04 | ||
图片预览




文档简介
(共27张PPT)
第13.3.1等腰三角形
(第1课时)
人教版数学八年级上册
1.了解等腰三角形的性质,体会等腰三角形“三线合一”的意义.
2.探索并掌握等腰三角形的性质,并用以解决实际问题.
学习目标
A
B
C
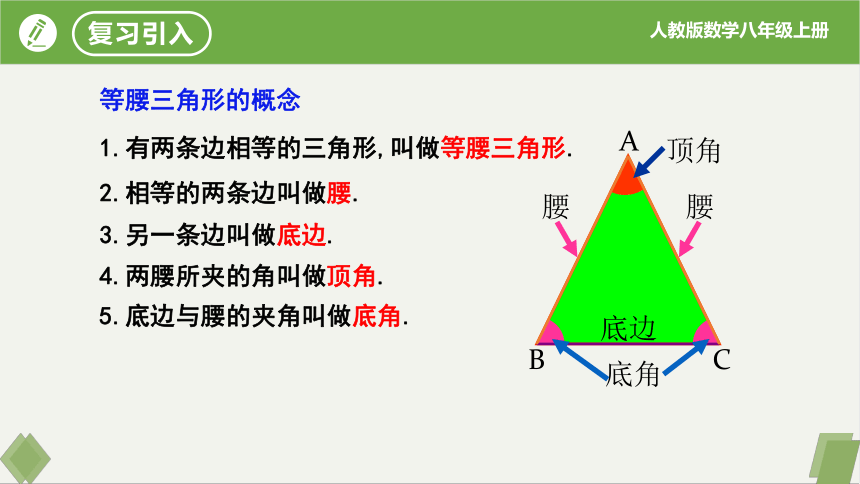
1.有两条边相等的三角形,叫做等腰三角形.
2.相等的两条边叫做腰.
3.另一条边叫做底边.
5.底边与腰的夹角叫做底角.
4.两腰所夹的角叫做顶角.
腰
腰
底边
顶角
底角
等腰三角形的概念
复习引入
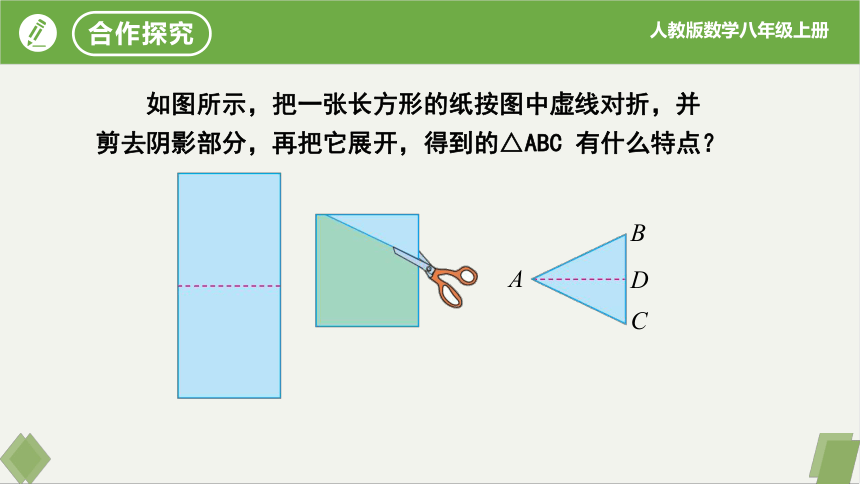
如图所示,把一张长方形的纸按图中虚线对折,并
剪去阴影部分,再把它展开,得到的△ABC 有什么特点?
A
B
C
D
合作探究
C
B
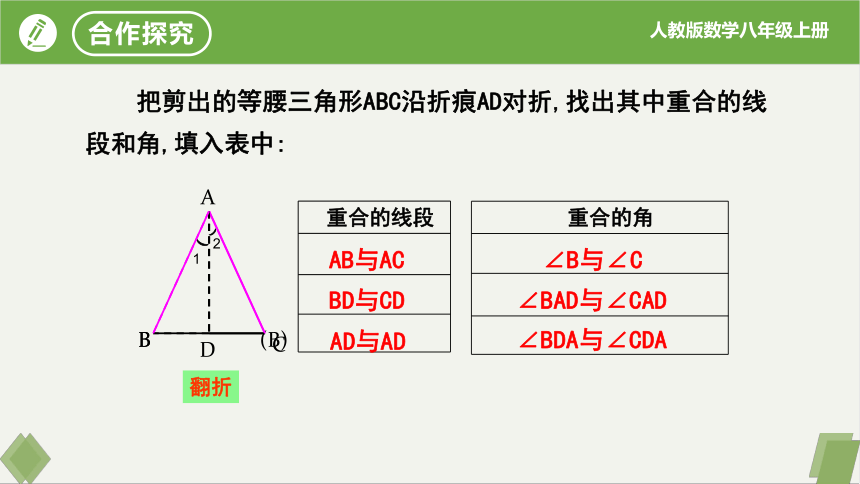
把剪出的等腰三角形ABC沿折痕AD对折,找出其中重合的线段和角,填入表中:
重合的角
重合的线段
∠B与∠C
∠BAD与∠CAD
∠BDA与∠CDA
(B)
A
B
D
翻折
BD与CD
AB与AC
AD与AD
1
2
合作探究
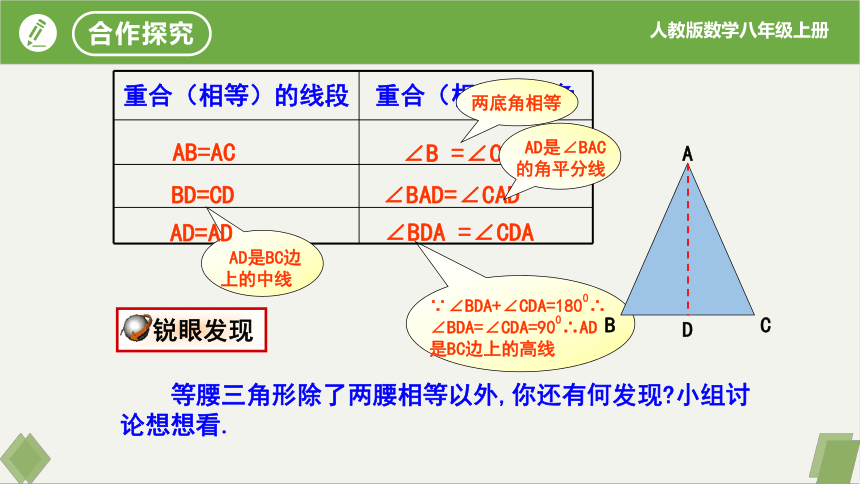
∵∠BDA+∠CDA=1800∴∠BDA=∠CDA=900∴AD是BC边上的高线
重合(相等)的线段 重合(相等)的角
A
C
B
D
AB=AC
BD=CD
∠B =∠C.
∠BAD=∠CAD
∠BDA =∠CDA
等腰三角形除了两腰相等以外,你还有何发现 小组讨论想想看.
锐眼发现
AD是BC边上的中线
AD是∠BAC的角平分线
两底角相等
AD=AD
合作探究
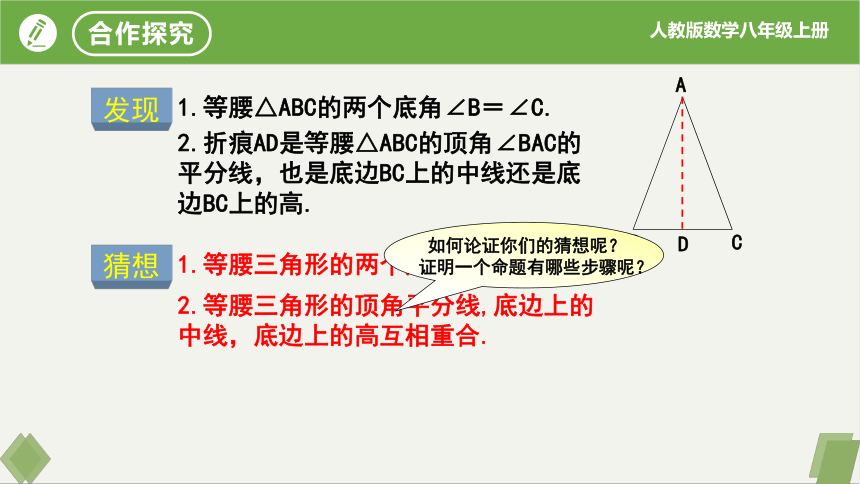
发现
2.折痕AD是等腰△ABC的顶角∠BAC的平分线,也是底边BC上的中线还是底边BC上的高.
A
B
C
D
猜想
1.等腰三角形的两个底角相等.
2.等腰三角形的顶角平分线,底边上的中线,底边上的高互相重合.
如何论证你们的猜想呢?
证明一个命题有哪些步骤呢?
1.等腰△ABC的两个底角∠B=∠C.
合作探究
已知:在△ABC中,AB=AC,求证:∠B= C.
分析:1.如何证明两个角相等?
2.如何构造两个全等的三角形?
1.等腰三角形的两个底角相等.
猜想
A
B
C
D
合作探究
Δ
Δ
Δ
Δ
解法一:已知如图ΔABC 中,AB =AC,求证:∠B =∠C.
A
B
C
D
合作探究
Δ
Δ
Δ
Δ
A
B
C
D
解法二:已知如图ΔABC 中,AB =AC,求证:∠B =∠C.
合作探究
Δ
Δ
Δ
Δ
A
B
C
D
解法三:已知如图ΔABC 中,AB =AC,求证:∠B =∠C.
合作探究
D
如图,作△ABC的中线AD
D
┌
如图,作△ABC
的高AD
D
如图,作顶角
的平分线AD.
A
B
C
A
B
C
A
B
C
等腰三角形常见辅助线
总结归纳
性质1:等腰三角形的两个底角相等.
(等边对等角)
符号语言:
在△ABC中
∵ AC=AB(已知)
∴ ∠B=∠C(等边对等角)
A
B
C
总结归纳
练习1.等腰三角形一个底角为80°,求它的顶角是_____.
20 °
变式1.等腰三角形一个角为70°,它的另外两个角为 __________________.
变式2.等腰三角形一个角为120°,它的另外两个角为_________.
30 °,30 °
70°,40°或55°,55°
小试牛刀
A
B
D
C
猜想
2.等腰三角形的顶角平分线,底边上的中线,底边上的高互相重合.
从猜想1的论证中,你有什么启发呢?
合作探究
③作∠A的角平分线AD
∴∠BAD=∠CAD
在△ABD和△ACD 中
AB=AC
∠BAD=∠CAD
AD=AD ∴△ABD≌△ACD (SAS)
∴BD=CD,∠ADB=∠ADC=90
∴AD是BC边上的中线,也是底边BC上的高
①作BC上的中线AD
∴BD=CD
在△ABD和△ACD中
AB=AC
AD=AD
BD=CD
∴△ABD≌△ACD (SSS)
∴∠BAD=∠CAD,
∠ADB=∠ADC=90°
∴AD是∠BAC的平分线,也是BC边上的高
②作AD⊥BC,垂足为D
∴ ∠ABD=∠ADC=90°
在△ABD和△ACD中
AB=AC
BD=CD
∴△ABD≌△ACD (HL)
∴BD=CD,∠BAD=∠CAD
∴AD是BC边上的中线,
也是∠BAC的平分线
证明:等腰三角形的顶角平分线,底边上的中线,底边上的高互相重合.
A
B
D
C
合作探究
符号语言:
(1)∵ 在△ABC中,AB = AC ,∠BAD = ∠CAD
∴ ⊥ , = ;
(2)∵在△ABC中, AB = AC,BD = CD
∴ ⊥ ,∴∠ = ∠ ;
(3)∵ 在△ABC中,AB = AC,AD⊥BC,
∴∠ =∠ , = .
性质2 :等腰三角形的顶角平分线、底边上的中线、底边上的高互相重合.(可简记为“三线合一”)
BAD CAD
BAD CAD
AD BC
AD BC
BD CD
BD CD
归纳:知一推二
总结归纳
A
B
D
C
小试牛刀
1.等腰三角形的一个角等于20°,则另外两个内角分别为( )
A.20°、140° B.20°、140°或80°、80°
C.80°、80° D.20°、80°
2.等腰三角形中,AB长是BC长2倍,三角形的周长是40,则AB的长为( )
A.20 B.16 C.20或16 D.18
B
B
例1 如图,在△ABC中 ,AB=AC,点D在AC上,且BD=BC=AD,求△ABC各角的度数。
1.图中有哪几个等腰三角形?
A
B
C
D
△ABC △ABD △BDC
2.有哪些相等的角?
∠ABC=∠ACB=∠BDC ∠ A=∠ABD
典例精析
例1 如图,在△ABC中 ,AB=AC,点D在AC上,且BD=BC=AD,求△ABC各角的度数。
x
x
2x
2x
2x
解:∵AB=AC,BD=BC=AD,
∴∠ABC=∠C=∠BDC,∠A=∠ABD(等边对等角)
设∠A=x,则∠BDC= ∠A+ ∠ABD=2x,
从而∠ABC= ∠C= ∠BDC=2x,
在 ABC中,
有∠A+∠ABC+∠C=x+2x+2x=180°,
解得x=36°,
在△ABC中, ∠A=36°,ABC=∠C=72°
典例精析
1.如图,在△ABC中,AB=AC,BD=CD,AD的延长线交BC于点E.求证:AE⊥BC.
证明:在△BAD与△CAD中
AB=AC
AD=AD
BD=CD
∴△BAD≌△CAD(SSS)
∴∠BAE=∠CAE
∵AB=AC
∴AE⊥BC
C
D
A
B
E
拓展训练
1.轴对称图形.
2.两个底角相等,简称“等边对等角”.
3.顶角平分线、底边上的中线、和底边上的高互相重合,简称“三线合 一”.
5.学习的数学思想及方法:分类讨论和一题多解.
课堂小结
等腰三角形:
4.解决等腰三角形问题时常用的辅助线.
1.如图,在△ABC中,已知AB=AC,D为BC的中点,∠BAD=35°,则∠C的度数为( )
A.35° B.45° C.55° D.60°
解:∵AB=AC,D为BC的中点,
∴∠B=∠C,AD⊥BC.
∵∠B=90°-∠BAD=55°,
∴∠C=55°.
C
课后作业
解:∵AB=AC=CD,
∴∠B=∠C,∠1=∠2.
∵BD=AD,
∴∠B=∠3.
∵∠1=∠B+∠3,∠B+∠3+∠2+∠C=180°,
∴∠B=36°,∠C=36°,∠BAC=108°.
2.如图,在△ABC中,点D在BC上,且有AB=AC=CD,BD=AD,求△ABC中各内角的度数.
1
3
2
A
B
C
D
课后作业
谢谢聆听
第13.3.1等腰三角形
(第1课时)
人教版数学八年级上册
1.了解等腰三角形的性质,体会等腰三角形“三线合一”的意义.
2.探索并掌握等腰三角形的性质,并用以解决实际问题.
学习目标
A
B
C
1.有两条边相等的三角形,叫做等腰三角形.
2.相等的两条边叫做腰.
3.另一条边叫做底边.
5.底边与腰的夹角叫做底角.
4.两腰所夹的角叫做顶角.
腰
腰
底边
顶角
底角
等腰三角形的概念
复习引入
如图所示,把一张长方形的纸按图中虚线对折,并
剪去阴影部分,再把它展开,得到的△ABC 有什么特点?
A
B
C
D
合作探究
C
B
把剪出的等腰三角形ABC沿折痕AD对折,找出其中重合的线段和角,填入表中:
重合的角
重合的线段
∠B与∠C
∠BAD与∠CAD
∠BDA与∠CDA
(B)
A
B
D
翻折
BD与CD
AB与AC
AD与AD
1
2
合作探究
∵∠BDA+∠CDA=1800∴∠BDA=∠CDA=900∴AD是BC边上的高线
重合(相等)的线段 重合(相等)的角
A
C
B
D
AB=AC
BD=CD
∠B =∠C.
∠BAD=∠CAD
∠BDA =∠CDA
等腰三角形除了两腰相等以外,你还有何发现 小组讨论想想看.
锐眼发现
AD是BC边上的中线
AD是∠BAC的角平分线
两底角相等
AD=AD
合作探究
发现
2.折痕AD是等腰△ABC的顶角∠BAC的平分线,也是底边BC上的中线还是底边BC上的高.
A
B
C
D
猜想
1.等腰三角形的两个底角相等.
2.等腰三角形的顶角平分线,底边上的中线,底边上的高互相重合.
如何论证你们的猜想呢?
证明一个命题有哪些步骤呢?
1.等腰△ABC的两个底角∠B=∠C.
合作探究
已知:在△ABC中,AB=AC,求证:∠B= C.
分析:1.如何证明两个角相等?
2.如何构造两个全等的三角形?
1.等腰三角形的两个底角相等.
猜想
A
B
C
D
合作探究
Δ
Δ
Δ
Δ
解法一:已知如图ΔABC 中,AB =AC,求证:∠B =∠C.
A
B
C
D
合作探究
Δ
Δ
Δ
Δ
A
B
C
D
解法二:已知如图ΔABC 中,AB =AC,求证:∠B =∠C.
合作探究
Δ
Δ
Δ
Δ
A
B
C
D
解法三:已知如图ΔABC 中,AB =AC,求证:∠B =∠C.
合作探究
D
如图,作△ABC的中线AD
D
┌
如图,作△ABC
的高AD
D
如图,作顶角
的平分线AD.
A
B
C
A
B
C
A
B
C
等腰三角形常见辅助线
总结归纳
性质1:等腰三角形的两个底角相等.
(等边对等角)
符号语言:
在△ABC中
∵ AC=AB(已知)
∴ ∠B=∠C(等边对等角)
A
B
C
总结归纳
练习1.等腰三角形一个底角为80°,求它的顶角是_____.
20 °
变式1.等腰三角形一个角为70°,它的另外两个角为 __________________.
变式2.等腰三角形一个角为120°,它的另外两个角为_________.
30 °,30 °
70°,40°或55°,55°
小试牛刀
A
B
D
C
猜想
2.等腰三角形的顶角平分线,底边上的中线,底边上的高互相重合.
从猜想1的论证中,你有什么启发呢?
合作探究
③作∠A的角平分线AD
∴∠BAD=∠CAD
在△ABD和△ACD 中
AB=AC
∠BAD=∠CAD
AD=AD ∴△ABD≌△ACD (SAS)
∴BD=CD,∠ADB=∠ADC=90
∴AD是BC边上的中线,也是底边BC上的高
①作BC上的中线AD
∴BD=CD
在△ABD和△ACD中
AB=AC
AD=AD
BD=CD
∴△ABD≌△ACD (SSS)
∴∠BAD=∠CAD,
∠ADB=∠ADC=90°
∴AD是∠BAC的平分线,也是BC边上的高
②作AD⊥BC,垂足为D
∴ ∠ABD=∠ADC=90°
在△ABD和△ACD中
AB=AC
BD=CD
∴△ABD≌△ACD (HL)
∴BD=CD,∠BAD=∠CAD
∴AD是BC边上的中线,
也是∠BAC的平分线
证明:等腰三角形的顶角平分线,底边上的中线,底边上的高互相重合.
A
B
D
C
合作探究
符号语言:
(1)∵ 在△ABC中,AB = AC ,∠BAD = ∠CAD
∴ ⊥ , = ;
(2)∵在△ABC中, AB = AC,BD = CD
∴ ⊥ ,∴∠ = ∠ ;
(3)∵ 在△ABC中,AB = AC,AD⊥BC,
∴∠ =∠ , = .
性质2 :等腰三角形的顶角平分线、底边上的中线、底边上的高互相重合.(可简记为“三线合一”)
BAD CAD
BAD CAD
AD BC
AD BC
BD CD
BD CD
归纳:知一推二
总结归纳
A
B
D
C
小试牛刀
1.等腰三角形的一个角等于20°,则另外两个内角分别为( )
A.20°、140° B.20°、140°或80°、80°
C.80°、80° D.20°、80°
2.等腰三角形中,AB长是BC长2倍,三角形的周长是40,则AB的长为( )
A.20 B.16 C.20或16 D.18
B
B
例1 如图,在△ABC中 ,AB=AC,点D在AC上,且BD=BC=AD,求△ABC各角的度数。
1.图中有哪几个等腰三角形?
A
B
C
D
△ABC △ABD △BDC
2.有哪些相等的角?
∠ABC=∠ACB=∠BDC ∠ A=∠ABD
典例精析
例1 如图,在△ABC中 ,AB=AC,点D在AC上,且BD=BC=AD,求△ABC各角的度数。
x
x
2x
2x
2x
解:∵AB=AC,BD=BC=AD,
∴∠ABC=∠C=∠BDC,∠A=∠ABD(等边对等角)
设∠A=x,则∠BDC= ∠A+ ∠ABD=2x,
从而∠ABC= ∠C= ∠BDC=2x,
在 ABC中,
有∠A+∠ABC+∠C=x+2x+2x=180°,
解得x=36°,
在△ABC中, ∠A=36°,ABC=∠C=72°
典例精析
1.如图,在△ABC中,AB=AC,BD=CD,AD的延长线交BC于点E.求证:AE⊥BC.
证明:在△BAD与△CAD中
AB=AC
AD=AD
BD=CD
∴△BAD≌△CAD(SSS)
∴∠BAE=∠CAE
∵AB=AC
∴AE⊥BC
C
D
A
B
E
拓展训练
1.轴对称图形.
2.两个底角相等,简称“等边对等角”.
3.顶角平分线、底边上的中线、和底边上的高互相重合,简称“三线合 一”.
5.学习的数学思想及方法:分类讨论和一题多解.
课堂小结
等腰三角形:
4.解决等腰三角形问题时常用的辅助线.
1.如图,在△ABC中,已知AB=AC,D为BC的中点,∠BAD=35°,则∠C的度数为( )
A.35° B.45° C.55° D.60°
解:∵AB=AC,D为BC的中点,
∴∠B=∠C,AD⊥BC.
∵∠B=90°-∠BAD=55°,
∴∠C=55°.
C
课后作业
解:∵AB=AC=CD,
∴∠B=∠C,∠1=∠2.
∵BD=AD,
∴∠B=∠3.
∵∠1=∠B+∠3,∠B+∠3+∠2+∠C=180°,
∴∠B=36°,∠C=36°,∠BAC=108°.
2.如图,在△ABC中,点D在BC上,且有AB=AC=CD,BD=AD,求△ABC中各内角的度数.
1
3
2
A
B
C
D
课后作业
谢谢聆听
