1.4.2第二课时有理数的加、减、乘、除混合运算 课件(22张PPT)
文档属性
| 名称 | 1.4.2第二课时有理数的加、减、乘、除混合运算 课件(22张PPT) |

|
|
| 格式 | pptx | ||
| 文件大小 | 2.8MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-09-12 00:00:00 | ||
图片预览






文档简介
(共22张PPT)
第1章
有理数
1.4.2 有理数的除法
第2课时
教学目标/Teaching aims
1
进一步理解有理数的加减乘除法则,能熟练地进行有理数的加减乘除运算.
2
通过有理数的加减乘除运算的学习,体会数
学知识的灵活运用.
复习回顾
1.有理数除法法则
两数相除,同号得__,异号得__,并把绝对值相__ . 0除以任何一个不等于0的数,都得__.
除以一个不等于0的数,等于乘这个数的___.
正
负
除
0
倒数
2.有理数除法的符号法则
新知探究
问题1:小学的四则混合运算的顺序是怎样的?
先乘除,后加减,同级运算从左至右,有括号先算括号内,再算括号外.括号计算顺序:先小括号,再中括号,最后大括号.
新知探究
问题2:我们目前都学习了哪些运算?
加法、减法、乘法、除法.
一个运算中,含有有理数的加、减、乘、除、等多种运算,称为有理数的混合运算.
新知探究
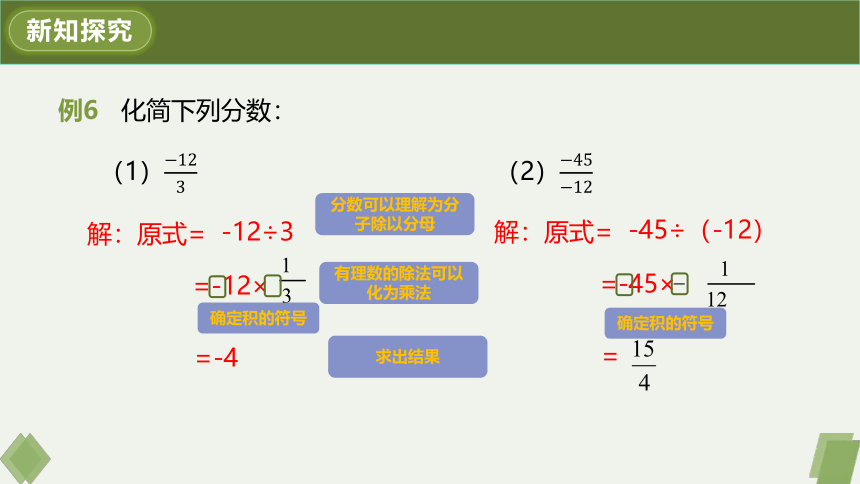
例6 化简下列分数:
(1) (2)
解:原式=
-12÷3
分数可以理解为分子除以分母
=-12×
=-4
有理数的除法可以化为乘法
求出结果
确定积的符号
解:原式=
-45÷(-12)
=-45×
=
确定积的符号
归纳小结
有理数的除法可以化为乘法,可以利用乘法的运算性质进行运算,乘除混合运算往往先将除法化为乘法,然后确定积的符号,最后求出结果。
巩固练习
例7 计算:
(1)
变成乘法,确定积的符号
巩固练习
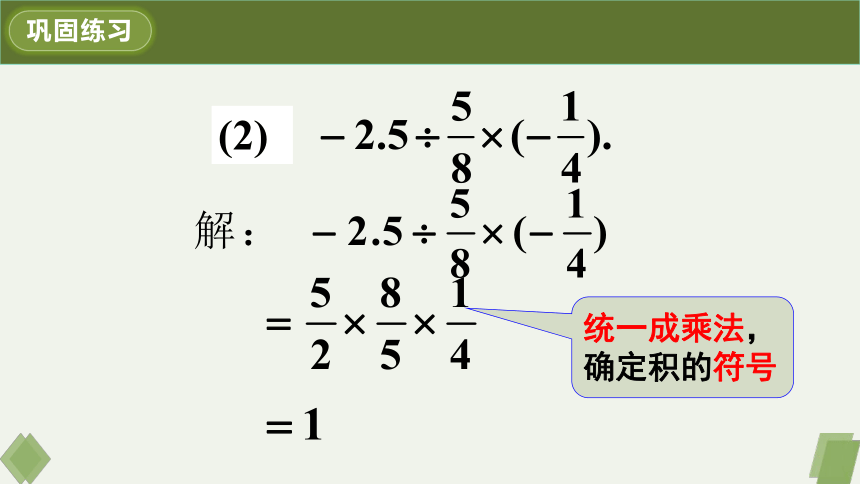
(2)
统一成乘法,确定积的符号
新知探究
观察式子 ,应该按照什么顺序来计算?
先算括号内的,再从左往右依次算乘除
归纳小结
先算乘除,再算加减,同级运算从左往右依次计算,如有括号,先算括号内的.
有理数混合运算的顺序:
新知应用
(1)(-8)+4÷(-2) (2)(-7)×(-5)-90÷(-15)
解:原式=(-8)+(-2)
=-10
解:原式=35-(-6)
=35+6
=41
巩固练习
例8. 计算:
(1)6-(-12)÷(-3) (2)3×(-4)+(-28)÷7
解:原式=6-4
=2
(3)(-48)÷8-(-25)×(-6) (4)
解:原式=-28+
=-25
解:原式=-12-4
=-16
解:原式=-6-150
=-156
新知探究
例9. 某公司去年1~3月平均每月亏损1.5万元,4~6月平均每月盈利2万元,7~10月平均每月盈利1.7万元,11~12月平均每月亏损2.3万元,这个公司去年总盈亏情况如何?
-1.5×3
2×3
1.7×4
-2.3×2
解:记盈利额为正数,亏损额为负数,公司去年全年总的盈亏(单位:万元)为
(-1.5)×3+2×3+1.7×4+(-2.3)×2
=-4.5+6+6.8-4.6
=3.7
答:这个公司去年全年盈利3.7万元
巩固练习
1.某公司去年1到3月份共亏损1.5万元,4到6月份共盈利2万元,7到10月份共盈利1.7万元,11到12月份共亏损2.3万元。这个公司去年总的盈亏情况如何?
解:记盈利额为正数,亏损额为负数,公司去年全年总的盈亏(单位:万元)为:
(-1.5)+2+1.7+(-2.3)
=0.1(万元)
答:这个公司去年全年盈利0.1万元.
新知探究
1. 计算器是一种方便实用的计算工具,用计算器进行比较复杂的计算比笔算要快捷得多.
2. 提倡在明确算理的情况下,恰当地使用计算器进行一些比较复杂的有理数加减乘除法的混合运算.
新知探究
例如可以用计算器计算例9中的
(-1.5)×3+2×3+1.7×4+(-2.3)×2
按键顺序依次为:
就可以得到答案:3.7
课堂练习
D
1. 下列各式中,结果相等的是( )
A.6÷(3×2)和 6÷3×2
B.(-120+400)÷20和-120+400÷20
C.-3-(4-7)和-3-4-7
D.-4×(2÷8)和-4×2÷8
课堂练习
2.下列运算结果等于1的是( )
A.(-3)+(-3) B.(-3)-(-3)
C.(-3)×(-3) D.(-3)÷(-3)
3.计算3-2×(-1)=( )
A.5 B.1 C.-1 D.6
D
A
课堂练习
4.计算:
(1)2×(-3÷ )-4×(-3)+15;
(2)-8+(-3)×[-4÷(- )+2]-32÷(-2).
解:(1)原式=2×(-27)-(-12)+15
=-54+12+15
=-27
(2)原式=-8+(-3)×(16+2)-9÷(-2)
=-8+(-3)×18-(-4.5)
=-8-54+4.5
=-57.5
课堂总结
有理数的加减乘除混合运算顺序:
先算乘除,再算加减,同级运算从左往右依次计算,如有括号,先算括号内的.
1.4.2 有理数的除法
第2课时
谢谢观看
有理数
第1章
有理数
1.4.2 有理数的除法
第2课时
教学目标/Teaching aims
1
进一步理解有理数的加减乘除法则,能熟练地进行有理数的加减乘除运算.
2
通过有理数的加减乘除运算的学习,体会数
学知识的灵活运用.
复习回顾
1.有理数除法法则
两数相除,同号得__,异号得__,并把绝对值相__ . 0除以任何一个不等于0的数,都得__.
除以一个不等于0的数,等于乘这个数的___.
正
负
除
0
倒数
2.有理数除法的符号法则
新知探究
问题1:小学的四则混合运算的顺序是怎样的?
先乘除,后加减,同级运算从左至右,有括号先算括号内,再算括号外.括号计算顺序:先小括号,再中括号,最后大括号.
新知探究
问题2:我们目前都学习了哪些运算?
加法、减法、乘法、除法.
一个运算中,含有有理数的加、减、乘、除、等多种运算,称为有理数的混合运算.
新知探究
例6 化简下列分数:
(1) (2)
解:原式=
-12÷3
分数可以理解为分子除以分母
=-12×
=-4
有理数的除法可以化为乘法
求出结果
确定积的符号
解:原式=
-45÷(-12)
=-45×
=
确定积的符号
归纳小结
有理数的除法可以化为乘法,可以利用乘法的运算性质进行运算,乘除混合运算往往先将除法化为乘法,然后确定积的符号,最后求出结果。
巩固练习
例7 计算:
(1)
变成乘法,确定积的符号
巩固练习
(2)
统一成乘法,确定积的符号
新知探究
观察式子 ,应该按照什么顺序来计算?
先算括号内的,再从左往右依次算乘除
归纳小结
先算乘除,再算加减,同级运算从左往右依次计算,如有括号,先算括号内的.
有理数混合运算的顺序:
新知应用
(1)(-8)+4÷(-2) (2)(-7)×(-5)-90÷(-15)
解:原式=(-8)+(-2)
=-10
解:原式=35-(-6)
=35+6
=41
巩固练习
例8. 计算:
(1)6-(-12)÷(-3) (2)3×(-4)+(-28)÷7
解:原式=6-4
=2
(3)(-48)÷8-(-25)×(-6) (4)
解:原式=-28+
=-25
解:原式=-12-4
=-16
解:原式=-6-150
=-156
新知探究
例9. 某公司去年1~3月平均每月亏损1.5万元,4~6月平均每月盈利2万元,7~10月平均每月盈利1.7万元,11~12月平均每月亏损2.3万元,这个公司去年总盈亏情况如何?
-1.5×3
2×3
1.7×4
-2.3×2
解:记盈利额为正数,亏损额为负数,公司去年全年总的盈亏(单位:万元)为
(-1.5)×3+2×3+1.7×4+(-2.3)×2
=-4.5+6+6.8-4.6
=3.7
答:这个公司去年全年盈利3.7万元
巩固练习
1.某公司去年1到3月份共亏损1.5万元,4到6月份共盈利2万元,7到10月份共盈利1.7万元,11到12月份共亏损2.3万元。这个公司去年总的盈亏情况如何?
解:记盈利额为正数,亏损额为负数,公司去年全年总的盈亏(单位:万元)为:
(-1.5)+2+1.7+(-2.3)
=0.1(万元)
答:这个公司去年全年盈利0.1万元.
新知探究
1. 计算器是一种方便实用的计算工具,用计算器进行比较复杂的计算比笔算要快捷得多.
2. 提倡在明确算理的情况下,恰当地使用计算器进行一些比较复杂的有理数加减乘除法的混合运算.
新知探究
例如可以用计算器计算例9中的
(-1.5)×3+2×3+1.7×4+(-2.3)×2
按键顺序依次为:
就可以得到答案:3.7
课堂练习
D
1. 下列各式中,结果相等的是( )
A.6÷(3×2)和 6÷3×2
B.(-120+400)÷20和-120+400÷20
C.-3-(4-7)和-3-4-7
D.-4×(2÷8)和-4×2÷8
课堂练习
2.下列运算结果等于1的是( )
A.(-3)+(-3) B.(-3)-(-3)
C.(-3)×(-3) D.(-3)÷(-3)
3.计算3-2×(-1)=( )
A.5 B.1 C.-1 D.6
D
A
课堂练习
4.计算:
(1)2×(-3÷ )-4×(-3)+15;
(2)-8+(-3)×[-4÷(- )+2]-32÷(-2).
解:(1)原式=2×(-27)-(-12)+15
=-54+12+15
=-27
(2)原式=-8+(-3)×(16+2)-9÷(-2)
=-8+(-3)×18-(-4.5)
=-8-54+4.5
=-57.5
课堂总结
有理数的加减乘除混合运算顺序:
先算乘除,再算加减,同级运算从左往右依次计算,如有括号,先算括号内的.
1.4.2 有理数的除法
第2课时
谢谢观看
有理数
