3.5三角形的内切圆课件

课件26张PPT。 3.5：三角形的内切圆亲爱的同学们:
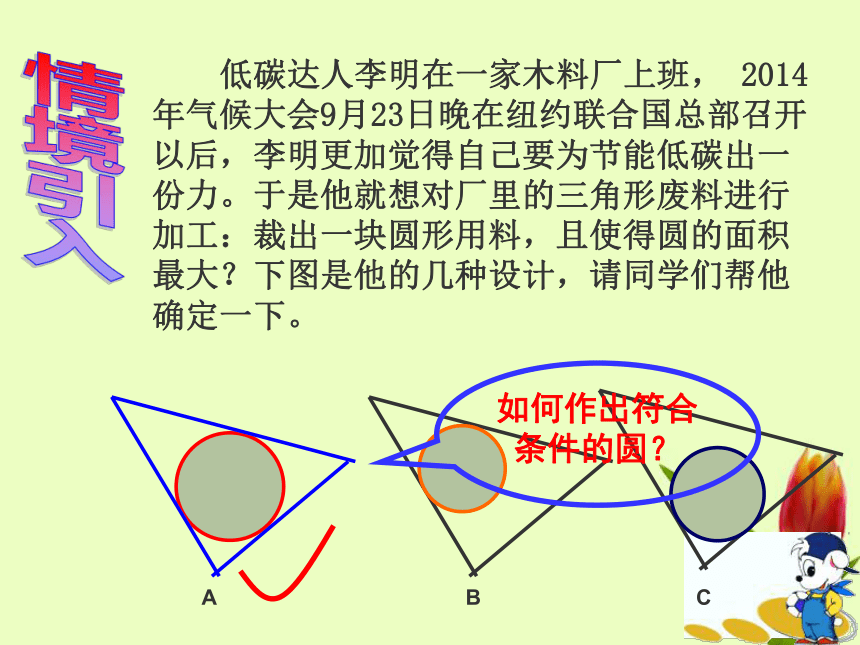
每一堂课都是一次知识的积累,每一次举手都是一次勇气的锻炼,让我们用勇气做翅膀,在知识的天空中自由翱翔 低碳达人李明在一家木料厂上班， 2014年气候大会9月23日晚在纽约联合国总部召开以后，李明更加觉得自己要为节能低碳出一份力。于是他就想对厂里的三角形废料进行加工：裁出一块圆形用料，且使得圆的面积最大？下图是他的几种设计，请同学们帮他确定一下。ABC情境引入如何作出符合条件的圆？三角形的内切圆课 题1、通过作图操作，识记三角形内切圆的定义 ；
2、通过作图和探索，体验并理解内心的性质；（重点）
3、类比三角形内切圆与三角形外接圆，进一步理解三角形内心和外心所具有的性质及应用 。（重点、难点）
学习目标易考点1. 确定圆的条件有哪两个？1）圆心 2）半径2. 角平分线的性质定理及其逆定理性质：角平分线上的点到这个角的两边的距离相等。
逆定理：到这个角的两边距离相等的点在这个角的平分线上。知识回顾思考并交流下列问题：1．“情境引入”中的圆与三角形三边的位置关系怎样？圆心到三角形三边的距离有什么特点？相切 相等?2．如图2，如果⊙O与△ABC的∠ABC的两边相切，且与∠ACB的两边也相切，那么⊙O的圆心怎么确定？圆心O是∠ABC与∠ACB的两个角平分线的交点. 探究一自主探究后，1号或2号负责指导有疑惑的同学能真正会做。 注意合作的有效性及纪律。
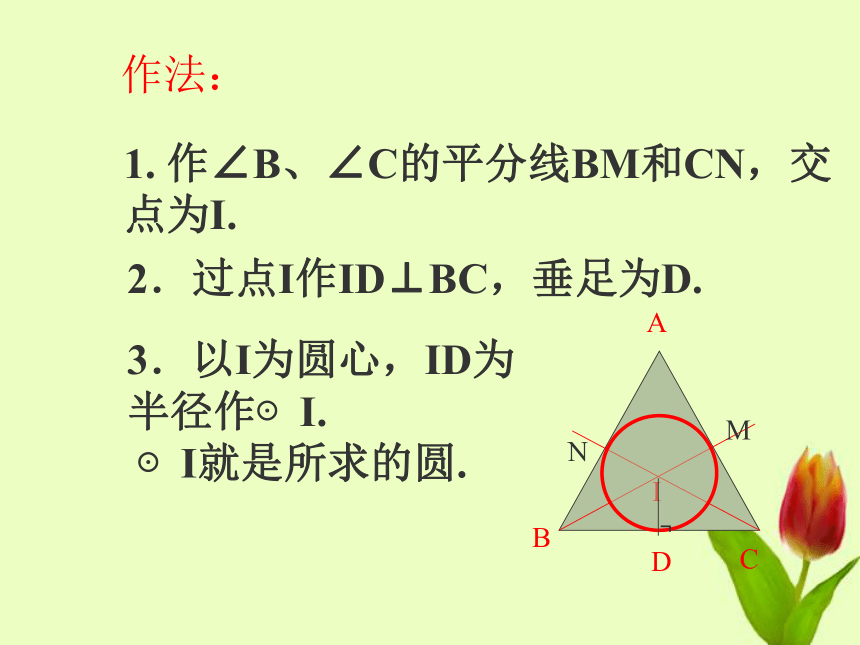
达标标准 ：至少1号，2号能独立探究解决，3号，4号在1号2号的指导下能做对。3．如何确定一个与三角形的三边都相切的圆的圆心的位置与半径的长？ 探究一4．你能利用尺规作图作出符合低碳达人李明作出的圆形用料吗 ？ 作法： ABC1. 作∠B、∠C的平分线BM和CN，交点为I. I2．过点I作ID⊥BC，垂足为D. 3．以I为圆心，ID为
半径作⊙I.
⊙I就是所求的圆. MN?4、思考：你能作出几个与一个三角形的三边都相切的圆？ 只能作一个，因为三角形的三条角
平分线交于一点，并且这点到三边的距离相等。1. 三角形的内切圆定义及其有关概念2.利用类比快速记忆三角形的外心和内心的性质： （1）定义：和三角形各边都 的圆叫做三角形的内切圆，内切圆的圆心叫做三角形的 ，这个三角形叫做圆的 三角形。
（2）性质：三角形的内心是三角形的三条 的交点，它到 的距离相等。内心和各顶点相连，则连线 各内角。探究二自主完成问题1后，快速记忆三角形的外心和内心的性质（2分钟）， 1号与4号互查，2号与3号互查。
达标标准 ：能记住并会用。相切内心外切角平分线各边平分三角形三边
垂直平分线
的交点1.OA=OB=OC
2.外心不一定在三角形的内部．三角形三条
角平分线的
交点1.到三边的距离
相等；
2.OA、OB、OC分别平分∠BAC、∠ABC、∠ACB
3.内心一定在三角形内部．运用时要明确“接”和“切”的含义、弄清“内心”与“外心”的区别。1. 三角形的内心到三角形各边的距离相等（ ）
2. 三角形的外心到三角形各顶点的距离相等 （ ）
3. 三角形的内心不一定在三角形的内部 （ ）
4. 一个三角形只有一个内切圆；一个圆也只有一个外切三角形（ ）
× × 跟踪训练：判断对错：√√如图,在△ABC中,∠A=68°,点I是内心,求∠BIC的度数 变式一： 若点I是外心呢？变式二：在△ABC中，点I是内心，
∠BIC=124°，求∠BAC的度数。1，已知△ABC的三边长分别为a，b，c，它的内切圆
半径为r，你会求△ABC的面积吗？2，已知Rt△ABC的两直角边和斜边分别
为a，b，c，你会求它的内切圆半
径r吗？（三）、探究活动：挑战自我组长组织本组合作完成，并记住结论。
达标标准：至少三人记住结论且会用。你有哪些收获呢？
与大家共分享！学而不思则罔回头一看，我想说…小结： 1.知识：

1.学习了三角形内切圆 及作法、三角形的内心、圆的外切三角形的概念．
2.三角形的内心
3.直角三角形内切圆半径公式。类比思想
2. 数学思想：1、下列命题正确的是（??）
A．三角形的内心到三角形三个顶点的距离相等
B．三角形的内心不一定在三角形的内部
C．等边三角形的内心，外心重合
D．一个圆一定有唯一一个外切三角形
达标检测C2、如图，⊙O内切于△ABC ，切点分别为D、E、F．已知∠B=50° ∠C=60° ，连结OE、OF、DE、DF，那么∠EDF=（ ）
A. 40 ° B. 55 ° C. 65 ° D. 70 °
达标检测B3、如图，△ABC的内切圆⊙O和各边分别相切于点D、E、F，则点O是△DEF的( )
A. 三条高的交点 B. 三条角平分线的交点
C. 三条中线的交点
三边垂直平分线的交点
4、边长为３，４，５
的三角形的内切圆半
径是＿＿，外接圆半
径是＿＿
达标检测D12.5我收获，我快乐完善学案，反思本节课你最大的收获是什么？你还有哪些困惑？再见 点I是△ABC的内心，线段AI的延长线交△ ABC的外接圆于点D，交BC边于点E．
求证：(1)ID=BD.
(2) ID2=DE?AD课后延伸：已知△ABC各边长分别为a、b、c，内切圆的半径为r，求这个三角形的面积.ODEFabc解：如图，连接OA、OB、OC
再分别作三边的高OD、OE、OF
垂足分别为D、E、F，
则有：
S△ABC=S△BOC+S△AOC+S△AOB
r点拨r如图:已知直角三角形的两直角边分别是a，b,斜边为c 则其内切圆的半径r为:F点拨 数学来源于生活，应用于生活。她会使你聪明,使你陶醉,使你成功。
同学们：
　 让数学成为我们的好朋友吧!达标要求：
本次达标测评共4个题：
4号做对3个即为达标，
3号做对3个即为达标，
2号做对4个即为达标，
1号做对4个即为达标。
做完后同桌互批,小组长做好统计 。