华师版数学八年级上册 11.2实数 课件(共22张PPT)
文档属性
| 名称 | 华师版数学八年级上册 11.2实数 课件(共22张PPT) |  | |
| 格式 | pptx | ||
| 文件大小 | 1.4MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 华东师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-09-12 17:54:22 | ||
图片预览








文档简介
(共22张PPT)
11.2 实数
第11章 数的开方
学习目标
了解无理数、实数的概念以及实数的两种分类,并能判断一个数是有理数还是无理数.
理解实数与数轴上的点一一对应的关系,知道实数的相反数、绝对值、运算法则以及运算律.
能对实数进行大小比较和四则混合运算.
复习导入
1.有理数如何分类?
有理数
整数
分数
按定义分类:
有理数
正有理数
零
负有理数
按性质分类:
2.把下列分数化为小数.
1.5
1.25
0.125
探究学习
1.414 213 562
1.414 213 562
1.999 999 999
近似值
无理数
(3)类似0.101 001 …(每两个1之间依次多1个0)这样的
无限不循环小数.
实数
1. 定义:
2. 分类:
(1)按定义分类
实数
有理数
无理数
正有理数
零
负有理数
正无理数
负无理数
有限小数或无限循环小数
无限不循环小数
有理数和无理数统称为实数.
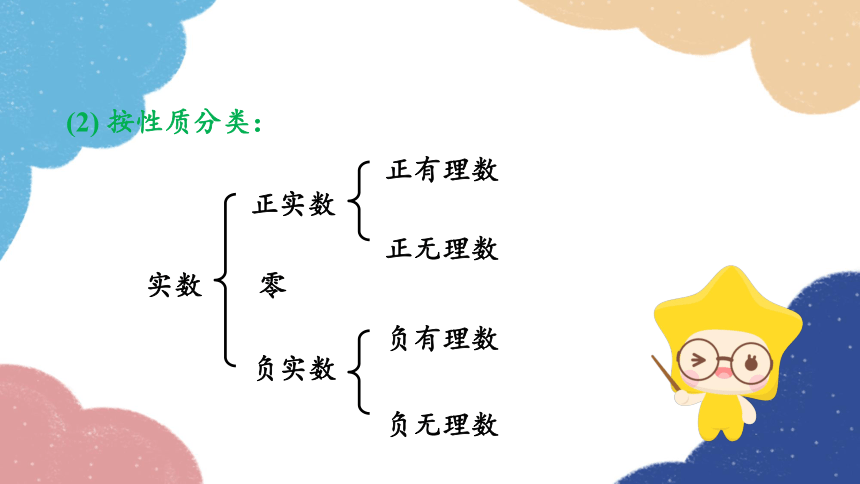
实数
正实数
零
负实数
(2) 按性质分类:
正有理数
正无理数
负有理数
负无理数
类比探究:每个有理数都可以用数轴上的点表示,那么无理数是否也可以用数轴上的点表示出来呢
如图,将两个边长为1的正方形分别沿对角线剪开,得到四个等腰直角三角形;
将其拼成一个大正方形.
2
-1
0
1
事实上,每一个无理数都可以用数轴上的一个点表示出来.
归纳总结
1.实数与数轴
(1)数轴上的每一个点必定表示一个实数;反过来,每一个
实数(有理数或无理数)都可以用数轴上的一个点来表示.
换句话说,实数与数轴上的点一一对应.
(2)对于数轴上的任意两个点,右边的点表示的数总比左边
的点表示的数大.
(3)数轴上两点间距离的求法:数轴上两点间的距离等于这
两点表示的数之差的绝对值.
典例精讲
-1
0
-2
-4
-3
-5
5
6
4
2
3
1
B
A
类比新知
2.概念与法则
(1)有理数的相反数和绝对值等概念同样适用于实数.
(2)实数的大小比较方法与有理数大小的比较方法相同:
①两个正实数比较大小绝对值大的较大;
②两个负实数比较大小绝对值大的反而小;
③正实数都大于0,负实数都小于0,即正实数>0>负实数.
(3)实数的运算与有理数的运算法则和运算律相同;
混合运算顺序为:先乘方、开方,再乘除,后加减.
例2 填空:
典例精讲
涉及无理数的大小比较和运算,通常可以取它们的近似值来进行.
取近似值计算时,中间结果通常要比要求的精确度多取一位.
随堂练习
1. 判断以下题目:
实数不是有理数就是无理数. ( )
无理数都是无限不循环小数. ( )
带根号的数都是无理数. ( )
无理数一定都带根号. ( )
两个无理数之积不一定是无理数. ( )
两个无理数之和一定是无理数. ( )
数轴上的任何一点都可以表示实数. ( )
A
C
C
-1
0
-2
5
4
2
3
1
解析:由图可知,覆盖的区域落在了正数部分,
B
= 1.14;
= 19.763 172
≈ 19.76.
课堂小结
1.无理数和实数的概念;
3.实数与数轴;
2.实数的分类;
4.实数的相反数、绝对值;
5.实数的大小比较;
6.实数的运算.
本节课你学会了哪些知识?
11.2 实数
第11章 数的开方
学习目标
了解无理数、实数的概念以及实数的两种分类,并能判断一个数是有理数还是无理数.
理解实数与数轴上的点一一对应的关系,知道实数的相反数、绝对值、运算法则以及运算律.
能对实数进行大小比较和四则混合运算.
复习导入
1.有理数如何分类?
有理数
整数
分数
按定义分类:
有理数
正有理数
零
负有理数
按性质分类:
2.把下列分数化为小数.
1.5
1.25
0.125
探究学习
1.414 213 562
1.414 213 562
1.999 999 999
近似值
无理数
(3)类似0.101 001 …(每两个1之间依次多1个0)这样的
无限不循环小数.
实数
1. 定义:
2. 分类:
(1)按定义分类
实数
有理数
无理数
正有理数
零
负有理数
正无理数
负无理数
有限小数或无限循环小数
无限不循环小数
有理数和无理数统称为实数.
实数
正实数
零
负实数
(2) 按性质分类:
正有理数
正无理数
负有理数
负无理数
类比探究:每个有理数都可以用数轴上的点表示,那么无理数是否也可以用数轴上的点表示出来呢
如图,将两个边长为1的正方形分别沿对角线剪开,得到四个等腰直角三角形;
将其拼成一个大正方形.
2
-1
0
1
事实上,每一个无理数都可以用数轴上的一个点表示出来.
归纳总结
1.实数与数轴
(1)数轴上的每一个点必定表示一个实数;反过来,每一个
实数(有理数或无理数)都可以用数轴上的一个点来表示.
换句话说,实数与数轴上的点一一对应.
(2)对于数轴上的任意两个点,右边的点表示的数总比左边
的点表示的数大.
(3)数轴上两点间距离的求法:数轴上两点间的距离等于这
两点表示的数之差的绝对值.
典例精讲
-1
0
-2
-4
-3
-5
5
6
4
2
3
1
B
A
类比新知
2.概念与法则
(1)有理数的相反数和绝对值等概念同样适用于实数.
(2)实数的大小比较方法与有理数大小的比较方法相同:
①两个正实数比较大小绝对值大的较大;
②两个负实数比较大小绝对值大的反而小;
③正实数都大于0,负实数都小于0,即正实数>0>负实数.
(3)实数的运算与有理数的运算法则和运算律相同;
混合运算顺序为:先乘方、开方,再乘除,后加减.
例2 填空:
典例精讲
涉及无理数的大小比较和运算,通常可以取它们的近似值来进行.
取近似值计算时,中间结果通常要比要求的精确度多取一位.
随堂练习
1. 判断以下题目:
实数不是有理数就是无理数. ( )
无理数都是无限不循环小数. ( )
带根号的数都是无理数. ( )
无理数一定都带根号. ( )
两个无理数之积不一定是无理数. ( )
两个无理数之和一定是无理数. ( )
数轴上的任何一点都可以表示实数. ( )
A
C
C
-1
0
-2
5
4
2
3
1
解析:由图可知,覆盖的区域落在了正数部分,
B
= 1.14;
= 19.763 172
≈ 19.76.
课堂小结
1.无理数和实数的概念;
3.实数与数轴;
2.实数的分类;
4.实数的相反数、绝对值;
5.实数的大小比较;
6.实数的运算.
本节课你学会了哪些知识?
