人教版数学八年级上册11.3.2 多边形的内角和课件(共17张PPT)
文档属性
| 名称 | 人教版数学八年级上册11.3.2 多边形的内角和课件(共17张PPT) |

|
|
| 格式 | ppt | ||
| 文件大小 | 3.1MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-09-12 00:00:00 | ||
图片预览






文档简介
(共17张PPT)
11.3.2 多边形的内角和
11.3 多边形及其内角和
复习提问:
1、什么三角形、多边形?
2、三角形的内角和、外角和各是多少?
探究:多边形的内角和
从刚才的计算中你发现什么?
边数每增加一条,内角和增加180°
例如三角形的内角和是180°,那么四边形的内角和是多少呢?
五边形的内角和是多少?比一比,看谁算得快?
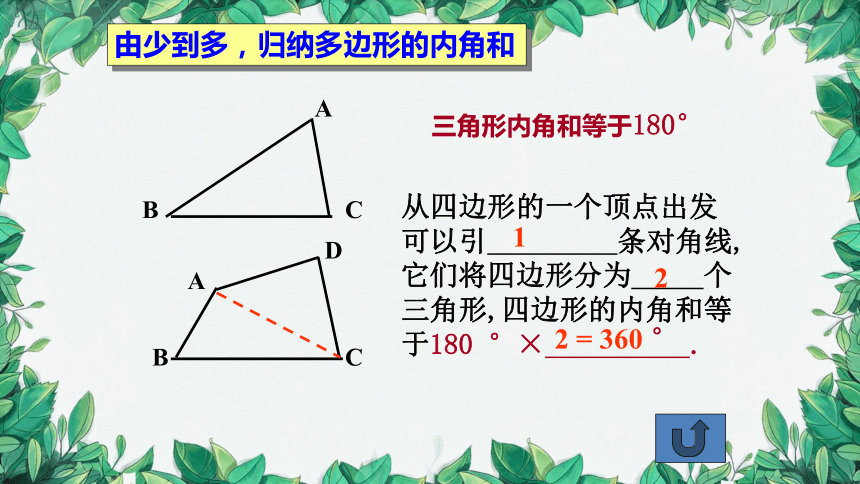
由少到多,归纳多边形的内角和
三角形内角和等于180°
A
B
C
A
C
D
B
从四边形的一个顶点出发可以引 条对角线,它们将四边形分为 个三角形,四边形的内角和等于180 °× .
2
2 = 360 °
1
由少到多,归纳多边形的内角和
三角形内角和等于1800
A
B
C
A
C
D
E
B
从五边形的一个顶点出发可以引 条对角线,它们将五边形分为 个三角形,五边形的内角和等于180 °× .
3
3 = 540 °
2
多边形
的边数 图 形 分割出的三角形的个数 多边形的
内 角 和
3
4
5
----- ------ ------ ------
n
n-2
1 1×180
2 2×180
3 3×180
(n-2)×180
研究多边形内角和问题的方法是:从简单入手---观察、归纳(寻找规律)---猜想结论---验证
n边形的内角和公式是:
(n-2)×180°
多边形的内角和与边数有关,
与形状、大小无关。
【课堂练习】
(1)五边形的内角和等于 ;
(2)十二边形的内角和等于 。
(3)若一个多边形的内角和为1080°,那么它是 边形;
(4)多边形的边数每增加一边,它的内角和就增加 ° 。
(5)正八边形的内角和等于 °,每一个内角等于 °。
540°
1800 °
10
1080
180
135
例1、如果一个四边形的一组对角互补,那么另一组对角有什么关系?
解:四边形ABCD中,
∠A+∠C=180°,
又因为 ∠A+∠B+∠C+∠D
=(4-2)×180°
=360°,
所以∠B+∠D=360°-(∠A+∠C)
=360°-180°
=180°
这就是说,如果一个四边形的一组对角互补,那么另一组对角也互补。
例题
D C
A B
例2、如图,在六边形的每个顶点处各取一个外角,
这些外角的和叫做六边形的外角和。
六边形的外角和等于多少?
思考:
1、任何一个外角同与它相邻的内角有什么关系?它们的和是多少度?
2、六边形的6个外角加上与它们相邻的6个内角,所得的总和是多少?
3、上述总和与六边形的内角和、外角和有什么关系?你能从中找到求六边形外角和的方法吗?
例题
提出问题
1、多边形的每一个外角与和它相邻的内角之间是什么关系?
2、一个n边形,它的内角和由边数n决定,那么它的外角和也由 边数n决定吗?
多边形的边数 3 4 5 6 … n
多边形的内角与外角的总和 3×180°=540° …
多边形的内角和 180° …
多边形的外角和 540°
-180°
=360° …
4×180°=720°
5×180°=900°
6×180°=1080°
360°
540°
720°
720°
-360°
=360°
900°
-540°
=360°
1080°
-720°
=360°
思考:
1、多边形的外角和与多边形的边数有关吗?内角和呢?
2、改变多边形的形状,它的外角和会改变吗?内角和呢?
归纳:多边形外角和=360°
若一个多边形的每个内角都是108°,则这个多边形的边数是 。
小比赛:看谁算得快!
解法1:
设它是n边形,则有:
n 180°=(n-2)×180°,
解得n=5
解法2:
360°÷(180°-108°)=5
【基础练习】
1、如果正多边形的一个外角为72°,那么它的边数是 。
2、正八边形的内角和为 ,外角和为 ,每个内角度数为 ,每个外角度数为 。
3、已知多边形的内角和与外角和相等,则这个多边形的边数为 。
【小结】说一说你的收获
1、多边形内角和公式为
(n-2)×180°,
所以:多边形的内角和一定是180°的倍数。
2、n边形n个外角的和为固定值360°,与边数无关。
11.3.2 多边形的内角和
11.3 多边形及其内角和
复习提问:
1、什么三角形、多边形?
2、三角形的内角和、外角和各是多少?
探究:多边形的内角和
从刚才的计算中你发现什么?
边数每增加一条,内角和增加180°
例如三角形的内角和是180°,那么四边形的内角和是多少呢?
五边形的内角和是多少?比一比,看谁算得快?
由少到多,归纳多边形的内角和
三角形内角和等于180°
A
B
C
A
C
D
B
从四边形的一个顶点出发可以引 条对角线,它们将四边形分为 个三角形,四边形的内角和等于180 °× .
2
2 = 360 °
1
由少到多,归纳多边形的内角和
三角形内角和等于1800
A
B
C
A
C
D
E
B
从五边形的一个顶点出发可以引 条对角线,它们将五边形分为 个三角形,五边形的内角和等于180 °× .
3
3 = 540 °
2
多边形
的边数 图 形 分割出的三角形的个数 多边形的
内 角 和
3
4
5
----- ------ ------ ------
n
n-2
1 1×180
2 2×180
3 3×180
(n-2)×180
研究多边形内角和问题的方法是:从简单入手---观察、归纳(寻找规律)---猜想结论---验证
n边形的内角和公式是:
(n-2)×180°
多边形的内角和与边数有关,
与形状、大小无关。
【课堂练习】
(1)五边形的内角和等于 ;
(2)十二边形的内角和等于 。
(3)若一个多边形的内角和为1080°,那么它是 边形;
(4)多边形的边数每增加一边,它的内角和就增加 ° 。
(5)正八边形的内角和等于 °,每一个内角等于 °。
540°
1800 °
10
1080
180
135
例1、如果一个四边形的一组对角互补,那么另一组对角有什么关系?
解:四边形ABCD中,
∠A+∠C=180°,
又因为 ∠A+∠B+∠C+∠D
=(4-2)×180°
=360°,
所以∠B+∠D=360°-(∠A+∠C)
=360°-180°
=180°
这就是说,如果一个四边形的一组对角互补,那么另一组对角也互补。
例题
D C
A B
例2、如图,在六边形的每个顶点处各取一个外角,
这些外角的和叫做六边形的外角和。
六边形的外角和等于多少?
思考:
1、任何一个外角同与它相邻的内角有什么关系?它们的和是多少度?
2、六边形的6个外角加上与它们相邻的6个内角,所得的总和是多少?
3、上述总和与六边形的内角和、外角和有什么关系?你能从中找到求六边形外角和的方法吗?
例题
提出问题
1、多边形的每一个外角与和它相邻的内角之间是什么关系?
2、一个n边形,它的内角和由边数n决定,那么它的外角和也由 边数n决定吗?
多边形的边数 3 4 5 6 … n
多边形的内角与外角的总和 3×180°=540° …
多边形的内角和 180° …
多边形的外角和 540°
-180°
=360° …
4×180°=720°
5×180°=900°
6×180°=1080°
360°
540°
720°
720°
-360°
=360°
900°
-540°
=360°
1080°
-720°
=360°
思考:
1、多边形的外角和与多边形的边数有关吗?内角和呢?
2、改变多边形的形状,它的外角和会改变吗?内角和呢?
归纳:多边形外角和=360°
若一个多边形的每个内角都是108°,则这个多边形的边数是 。
小比赛:看谁算得快!
解法1:
设它是n边形,则有:
n 180°=(n-2)×180°,
解得n=5
解法2:
360°÷(180°-108°)=5
【基础练习】
1、如果正多边形的一个外角为72°,那么它的边数是 。
2、正八边形的内角和为 ,外角和为 ,每个内角度数为 ,每个外角度数为 。
3、已知多边形的内角和与外角和相等,则这个多边形的边数为 。
【小结】说一说你的收获
1、多边形内角和公式为
(n-2)×180°,
所以:多边形的内角和一定是180°的倍数。
2、n边形n个外角的和为固定值360°,与边数无关。
