初中数学人教版九下29.2三视图(第3课时) 课件(共21张PPT)
文档属性
| 名称 | 初中数学人教版九下29.2三视图(第3课时) 课件(共21张PPT) |

|
|
| 格式 | pptx | ||
| 文件大小 | 318.2KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-09-12 18:02:31 | ||
图片预览



文档简介
(共21张PPT)
29.2 三视图
(第3课时)
第二十九章 投影与视图
学习目标
1.探索三视图、实物(几何体)、展开图三者之间的转化关系.(重点)
2.利用三视图中的数据信息进行计算或计数.(难点)
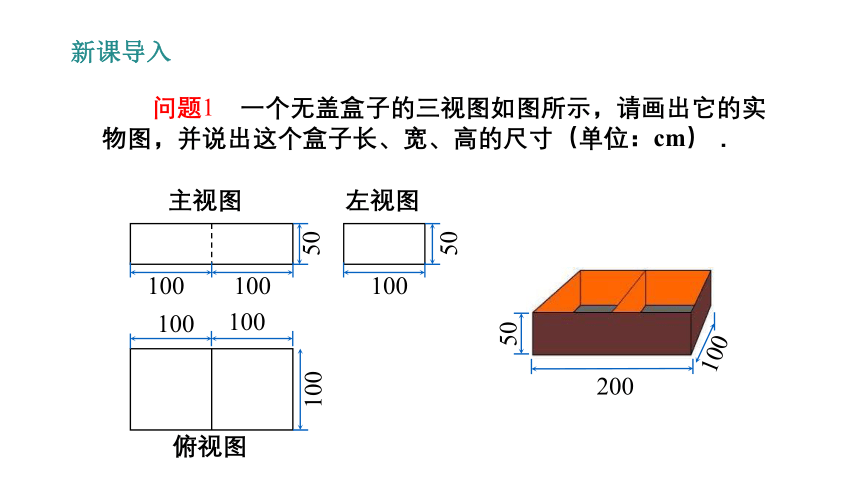
问题1 一个无盖盒子的三视图如图所示,请画出它的实物图,并说出这个盒子长、宽、高的尺寸(单位:cm).
主视图
左视图
俯视图
100
50
100
100
100
100
50
100
100
200
50
新课导入
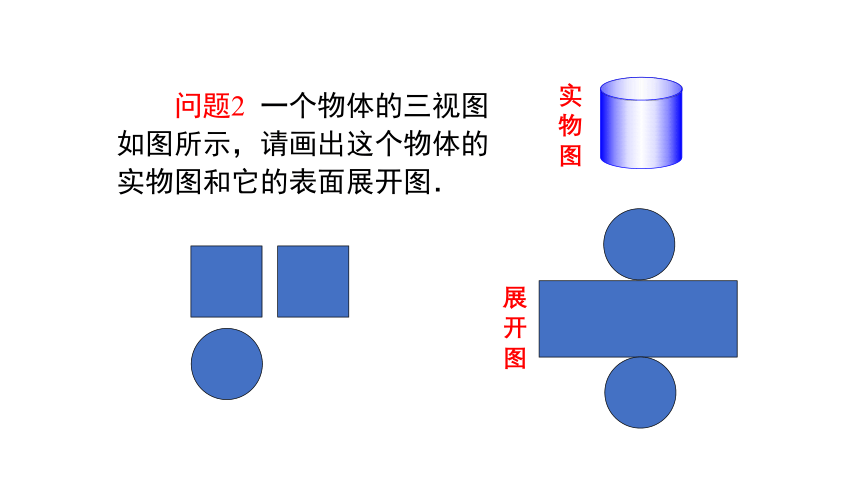
展开图
实物图
问题2 一个物体的三视图如图所示,请画出这个物体的实物图和它的表面展开图.
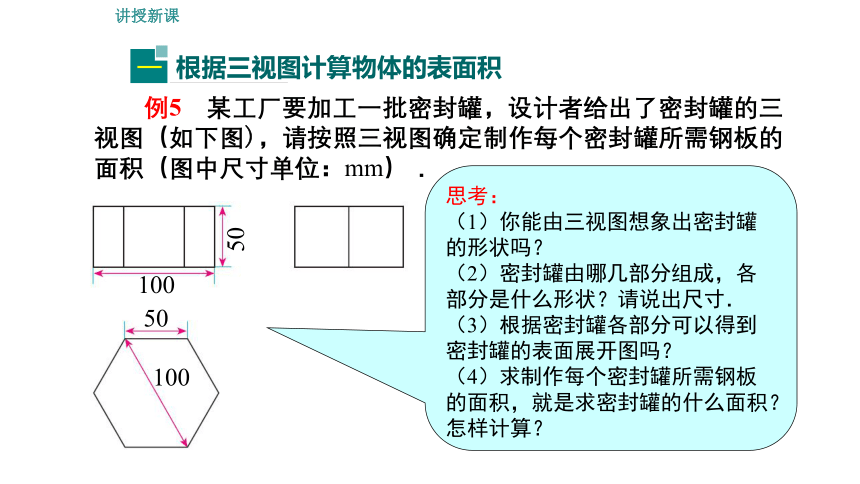
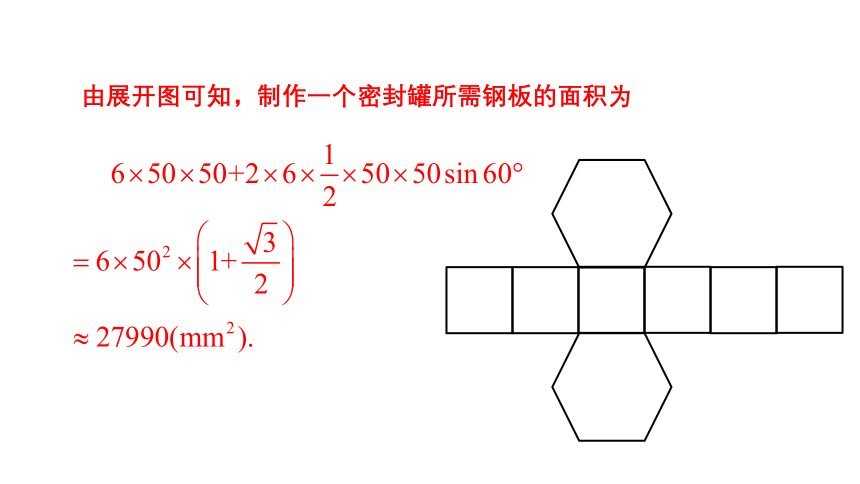
例5 某工厂要加工一批密封罐,设计者给出了密封罐的三视图(如下图),请按照三视图确定制作每个密封罐所需钢板的面积(图中尺寸单位:mm).
100
50
50
100
讲授新课
根据三视图计算物体的表面积
一
思考:
(1)你能由三视图想象出密封罐的形状吗?
(2)密封罐由哪几部分组成,各部分是什么形状?请说出尺寸.
(3)根据密封罐各部分可以得到密封罐的表面展开图吗?
(4)求制作每个密封罐所需钢板的面积,就是求密封罐的什么面积?怎样计算?
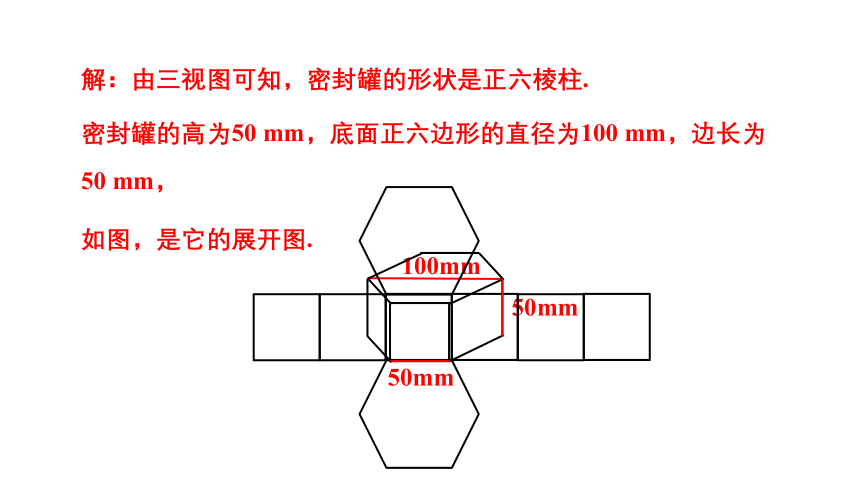
解:由三视图可知,密封罐的形状是正六棱柱.
50mm
50mm
密封罐的高为50 mm,底面正六边形的直径为100 mm,边长为50 mm,
100mm
如图,是它的展开图.
由展开图可知,制作一个密封罐所需钢板的面积为
三视图
立体图形
展开图
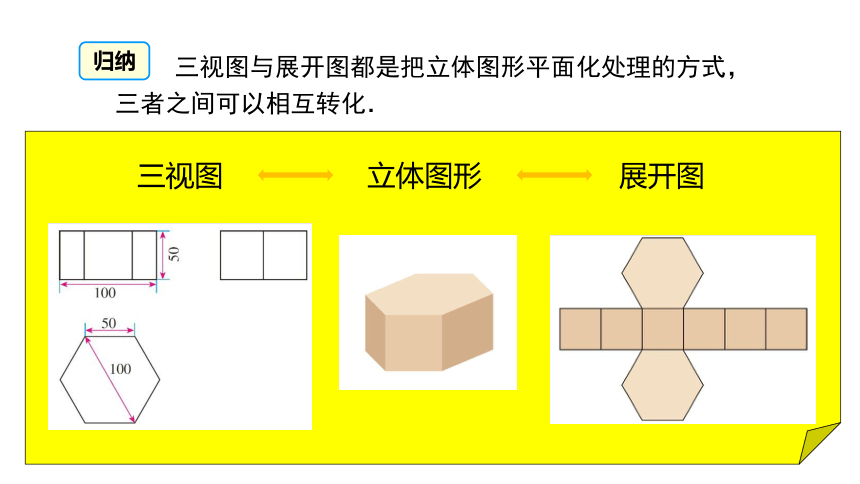
归纳
三视图与展开图都是把立体图形平面化处理的方式,三者之间可以相互转化.
总结
①立体化:根据给出的三视图得到立体图形,并确定立体图形的长、宽、高;
②平面化:将立体图形展开得到表面展开图,观察它的组成部分;
③数量化:根据展开图的相应数据,求出展开图的面积,即得几何体的表面积.
由三视图求几何体表面积的一般步骤
3
2
1
由几个相同的小正方体搭成的几何体的三视图如图所示,那么几何体中一共有几个小正方体?
根据视图求小正方体的数量
二
探索:
(1)画图描述几何体的形状.
(2)在如图所示的行列图中,填上每部分的小正方体个数.
(3)这个几何体中一共有几个小正方体?
1
(1)如图,根据主视图和俯视图,能确定小正方体个数吗?请画行列图中填上数据说明.
思考
有俯视图的直接用它作为行列图
主视图
俯视图
由主视图可知左侧位置1个,右侧最多3个
此处可有1,2或3个
右侧至少一个方格的位置上有3个,可假设此处有3个
小正方体有1+3+1=5(个),或者1+3+2=6(个),
或者1+3+3=7(个).
3
(2)根据左视图和俯视图,能确定小正方体个数吗?请画行列图中填上数据说明.
俯视图
左视图
2
有俯视图的直接用它作为行列图
由左视图可知后排最多3个,前排位置2个
此处可有1,2或3个
后排至少一个方格的位置上有3个,可假设此处有3个
小正方体有2+3+1=6(个),或者2+3+2=7(个),
或者2+3+3=8(个).
3
(3)如图1,根据主视图和左视图,能确定小正方体个数吗?请在行列图中填上数据说明.
主视图
左视图
前后两行,前排最多2个,后排最多3个
左右两列,左侧最多1个,右侧最多3个
结合两个视图可知,此处有3个
小正方体有1+3+2+0=6(个),或者1+3+2+1=7(个).
此处有0或1个
3
2
1
结合两个视图可知,此处有2个
左侧最多1个,假设此处1个
归纳
对于在小正方体组成的几何体,结合左视图或主视图,在俯视图中标注出位于每一个位置上小正方体的层数,从而得到所有小正方体的数量;
反之,由俯视图中标注的层数,能想象出几何体的形状,从而得到左视图和主视图.
小正方体组成几何体的视图与数量关系
1.教材第100页练习第1(1)题,第2题.
课堂练习
2.如图,是由一些棱长为1cm的小正方体
构成的立体图形的三种视图,那么这个
立体图形的表面积是( )
A.12 B.14
C.16 D.18
表面积为:2×(2+2+3)=14(cm2),故选B.
B
3.几个相同的正方体叠合在一起,该组合体的主视图和俯视图如图所示,那么组合体中正方体的个数最少有几个?最多有几个?
解:正方体最少的情况如图1所示,
此时正方体有1×4+2×2=8(个);
正方体最多的情况如图2所示,
此时正方体有1×2+2×4=10(个).
1
2
2
2
2
1
图2
1
2
2
1
1
1
图1
课堂小结
1.由三视图求几何体的体积或表面积,一般步骤是怎样的?
2.对于在小正方体组成的几何体,怎样通过三视图或其中两个视图,判断小正方体的个数?
3.做三视图与表面展开图,都是把立体图形转化为平面图形,那么三视图、立体图与展开图三者之间有什么关系?
三视图
立体图形
展开图
表面积
体积
组成的小正方体个数
布置作业
A组:教材第102页习题29.2第5,9,10题.
B组:1.由若干个相同的小正方体搭成的一个几何体的主视图和俯视图如图所示,则组成这个几何体的小正方体的个数是_________.
2. 根据三视图描述物体的形状,试画出物体的表面展开图.
主视图
俯视图
左视图
3.在某儿童游乐园门口需要修建一个由正方体和圆柱组合而成的立体图形,如图所示,已知正方体的棱长与圆柱的直径及高相等,都是 1 m.
(1)请画出该立体图形的三视图;
(2)为了好看,需要在该立体图形表面刷一层油漆,已知油漆每平方米30元,那么一共需要花费多少元?(结果精确到0.1)
29.2 三视图
(第3课时)
第二十九章 投影与视图
学习目标
1.探索三视图、实物(几何体)、展开图三者之间的转化关系.(重点)
2.利用三视图中的数据信息进行计算或计数.(难点)
问题1 一个无盖盒子的三视图如图所示,请画出它的实物图,并说出这个盒子长、宽、高的尺寸(单位:cm).
主视图
左视图
俯视图
100
50
100
100
100
100
50
100
100
200
50
新课导入
展开图
实物图
问题2 一个物体的三视图如图所示,请画出这个物体的实物图和它的表面展开图.
例5 某工厂要加工一批密封罐,设计者给出了密封罐的三视图(如下图),请按照三视图确定制作每个密封罐所需钢板的面积(图中尺寸单位:mm).
100
50
50
100
讲授新课
根据三视图计算物体的表面积
一
思考:
(1)你能由三视图想象出密封罐的形状吗?
(2)密封罐由哪几部分组成,各部分是什么形状?请说出尺寸.
(3)根据密封罐各部分可以得到密封罐的表面展开图吗?
(4)求制作每个密封罐所需钢板的面积,就是求密封罐的什么面积?怎样计算?
解:由三视图可知,密封罐的形状是正六棱柱.
50mm
50mm
密封罐的高为50 mm,底面正六边形的直径为100 mm,边长为50 mm,
100mm
如图,是它的展开图.
由展开图可知,制作一个密封罐所需钢板的面积为
三视图
立体图形
展开图
归纳
三视图与展开图都是把立体图形平面化处理的方式,三者之间可以相互转化.
总结
①立体化:根据给出的三视图得到立体图形,并确定立体图形的长、宽、高;
②平面化:将立体图形展开得到表面展开图,观察它的组成部分;
③数量化:根据展开图的相应数据,求出展开图的面积,即得几何体的表面积.
由三视图求几何体表面积的一般步骤
3
2
1
由几个相同的小正方体搭成的几何体的三视图如图所示,那么几何体中一共有几个小正方体?
根据视图求小正方体的数量
二
探索:
(1)画图描述几何体的形状.
(2)在如图所示的行列图中,填上每部分的小正方体个数.
(3)这个几何体中一共有几个小正方体?
1
(1)如图,根据主视图和俯视图,能确定小正方体个数吗?请画行列图中填上数据说明.
思考
有俯视图的直接用它作为行列图
主视图
俯视图
由主视图可知左侧位置1个,右侧最多3个
此处可有1,2或3个
右侧至少一个方格的位置上有3个,可假设此处有3个
小正方体有1+3+1=5(个),或者1+3+2=6(个),
或者1+3+3=7(个).
3
(2)根据左视图和俯视图,能确定小正方体个数吗?请画行列图中填上数据说明.
俯视图
左视图
2
有俯视图的直接用它作为行列图
由左视图可知后排最多3个,前排位置2个
此处可有1,2或3个
后排至少一个方格的位置上有3个,可假设此处有3个
小正方体有2+3+1=6(个),或者2+3+2=7(个),
或者2+3+3=8(个).
3
(3)如图1,根据主视图和左视图,能确定小正方体个数吗?请在行列图中填上数据说明.
主视图
左视图
前后两行,前排最多2个,后排最多3个
左右两列,左侧最多1个,右侧最多3个
结合两个视图可知,此处有3个
小正方体有1+3+2+0=6(个),或者1+3+2+1=7(个).
此处有0或1个
3
2
1
结合两个视图可知,此处有2个
左侧最多1个,假设此处1个
归纳
对于在小正方体组成的几何体,结合左视图或主视图,在俯视图中标注出位于每一个位置上小正方体的层数,从而得到所有小正方体的数量;
反之,由俯视图中标注的层数,能想象出几何体的形状,从而得到左视图和主视图.
小正方体组成几何体的视图与数量关系
1.教材第100页练习第1(1)题,第2题.
课堂练习
2.如图,是由一些棱长为1cm的小正方体
构成的立体图形的三种视图,那么这个
立体图形的表面积是( )
A.12 B.14
C.16 D.18
表面积为:2×(2+2+3)=14(cm2),故选B.
B
3.几个相同的正方体叠合在一起,该组合体的主视图和俯视图如图所示,那么组合体中正方体的个数最少有几个?最多有几个?
解:正方体最少的情况如图1所示,
此时正方体有1×4+2×2=8(个);
正方体最多的情况如图2所示,
此时正方体有1×2+2×4=10(个).
1
2
2
2
2
1
图2
1
2
2
1
1
1
图1
课堂小结
1.由三视图求几何体的体积或表面积,一般步骤是怎样的?
2.对于在小正方体组成的几何体,怎样通过三视图或其中两个视图,判断小正方体的个数?
3.做三视图与表面展开图,都是把立体图形转化为平面图形,那么三视图、立体图与展开图三者之间有什么关系?
三视图
立体图形
展开图
表面积
体积
组成的小正方体个数
布置作业
A组:教材第102页习题29.2第5,9,10题.
B组:1.由若干个相同的小正方体搭成的一个几何体的主视图和俯视图如图所示,则组成这个几何体的小正方体的个数是_________.
2. 根据三视图描述物体的形状,试画出物体的表面展开图.
主视图
俯视图
左视图
3.在某儿童游乐园门口需要修建一个由正方体和圆柱组合而成的立体图形,如图所示,已知正方体的棱长与圆柱的直径及高相等,都是 1 m.
(1)请画出该立体图形的三视图;
(2)为了好看,需要在该立体图形表面刷一层油漆,已知油漆每平方米30元,那么一共需要花费多少元?(结果精确到0.1)
