初中数学北师大七上 4.4角的比较 课件(共17张PPT)
文档属性
| 名称 | 初中数学北师大七上 4.4角的比较 课件(共17张PPT) |

|
|
| 格式 | pptx | ||
| 文件大小 | 910.0KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-09-12 00:00:00 | ||
图片预览





文档简介
(共17张PPT)
第四章 基本平面图形
4.4 角的比较
学习目标
1.经历比较角的大小的研究过程,体会角的比较和线段的比较方法的一致性.
2.会比较角的大小,能估计一个角的大小.
3.在操作活动中认识角的平分线,能画出一个角的平分线.
温故知新
1、角是怎样定义的?
定义1:由两条具有公共端点的射线所组成的图形叫角.
定义2:一条射线绕它的端点旋转所组成的图形叫角.
2、怎样来表示一个角?
表示方法(1):用三个大写字母表示;∠AOB
表示方法(2):用一个大写字母表示;∠A
表示方法(3):用一个阿拉伯数字表示;∠1
表示方法(4):用一个希腊字母表示;∠β
每种方法应注意什么问题?
温故知新
3、角是如何分类的
按角的大小可分为:直角、锐角、钝角、平角、周角
4、如何度量一个角?角的单位是什么?如何换算?
可用量角器度量一个角.角的单位是度、分、秒. 1度=60分 1分=60秒
5.线段长短的比较
叠合法、度量法
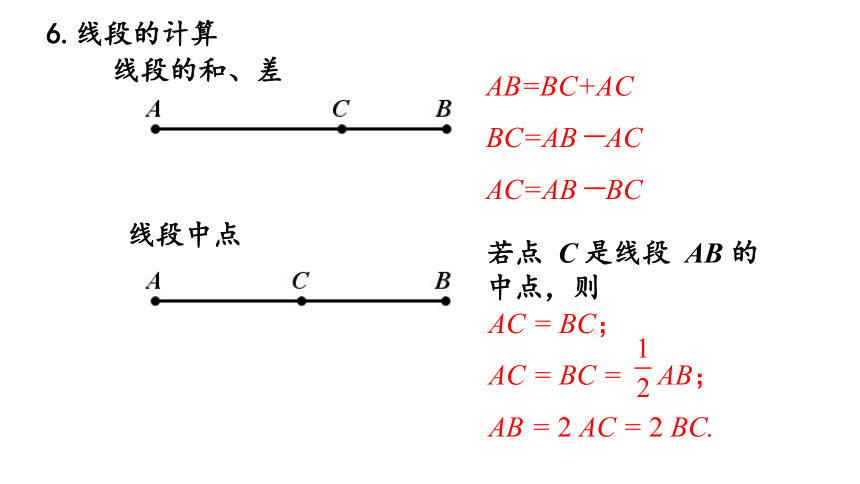
AB=BC+AC
BC=AB-AC
AC=AB-BC
线段的和、差
线段中点
若点 C 是线段 AB 的中点,则
AC = BC;
AC = BC = AB;
AB = 2 AC = 2 BC.
6.线段的计算
问题探究
知识点一:角的大小比较方法
(1)度量法:用量角器量出角的________, 根据度数比较大小.
∠1=30°,∠2=60°,∠1<∠2
度数
问题:
我们知道角是可以度量的,也就是说角是有大小的,你认为角的大小与什么有关?如何比较角的大小?
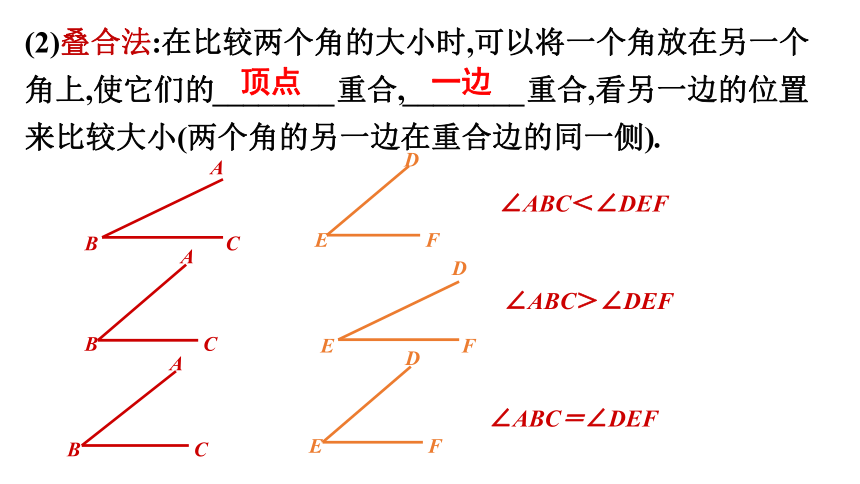
(2)叠合法:在比较两个角的大小时,可以将一个角放在另一个角上,使它们的________重合,________重合,看另一边的位置来比较大小(两个角的另一边在重合边的同一侧).
顶点
一边
∠ABC<∠DEF
A
B
C
D
E
F
D
E
F
A
B
C
D
E
F
A
B
C
∠ABC>∠DEF
∠ABC=∠DEF
角的大小指角的两边所张开的角的度数,与角的边的“长”“短”无关!
角既然有大小,那么它就有和、差、倍、分的关系!
注意下面的符号语言:
∠AOB=∠AOC+∠BOC
∠AOC=∠AOB-∠BOC
∠BOC=∠AOB-∠AOC
C
B
O
A
知识要点
在一张纸上画一个角∠AOB, 把纸对折,让角的两边OA与OB重合, 展开后沿折痕画一条射线, 这条射线把这个角分成两部分,这两部分角的大小一样吗?
角平分线定义:
C
B
O
A
从一个角的顶点引出的一条射线,
把这个角分成两个相等的角,这条射
线叫这个角的平分线.
几何语言:
∵OC平分∠AOB,
∴∠AOC=∠BOC
问题探究
例 如图,∠AOB=120°,OD平分∠BOC,OE平分∠AOC.
(1)求∠EOD的度数;
(2)若∠BOC=90°,求∠AOE的度数.
解:(1)∵∠AOB=120°,OD平分∠BOC,OE平分∠AOC,
∴∠EOD=∠DOC+∠EOC=(∠BOC+∠AOC)=∠AOB=×120°=60°.
(2) ∵ ∠AOB=120°,∠BOC=90°,
∴∠AOC=120°-90°=30°,
∵ OE平分∠AOC,
∴∠AOE=∠AOC=×30°=15°.
典例解析
1.下列说法中,正确的是( )
A.角的平分线就是把一个角分成两个角的射线
B.若∠AOB=∠AOC,则OA是∠AOC的平分线
C.角的大小与它的边的长短无关
D.∠CAD与∠BAC的和一定是∠BAD
C
课堂演练
2.如图1,O为直线AB上一点,OD平分∠BOC,若∠BOC=60°,则∠COD的大小为( )
A.120° B.30° C.60° D.150°
B
3.如图2,已知O是直线AB上一点,∠1=40°,OD平分∠BOC,则∠2的度数是________.
70°
4.如图,借助一副三角尺可以画出15°和75°的角,你还能画出哪些度数的角?
75°
15°
15°, 30°, 45°, 60°, 75°, 90°, 105°, 120°, 135°, 150°, 165°.
5.把一副三角尺按如图所示方式拼在一起.
(1)写出∠A,∠B,∠BCD,∠D,∠AED的度数;
(2)用“<”将上述各角连接起来.
解:(1)∠A=30°,∠B=90°,∠BCD=150°,∠D=45°,∠AED=135°.
(2)∠A<∠D<∠B<∠AED<∠BCD.
6.如图,OB是∠AOC的平分线,OD是∠COE的平分线,如果∠AOB=40°,∠COE=60°,那么∠BOD的度数是_____.
70°
7.如图,OC是∠AOB的平分线,∠BOD=∠DOC,∠BOD=10°,则∠AOD的度数为( )
A.50° B.60° C.70° D.80°
C
解:∵点O在直线AB上,
∴∠AOB=∠AOC+∠BOC=180°.
∵ ∠AOC=130°,
∴∠BOC=50°.
∵ OB平分∠COD,所以∠COD=2∠COB=100°.
∴∠AOD=360°-∠AOC-∠COD=360°-130°100°=130°.
∵ OE平分∠AOD,
∴∠AOE=∠AOD=65°.
8.如图,点O是直线AB上的一点,∠AOC=130°,OB平分∠COD,OE平分∠AOD,求∠AOE的度数.
角的大小比较
度量法、叠合法
角的和差
角的平分线
图形语言、文字语言、符号语言
方 法
作 法
描 述
课堂小结
第四章 基本平面图形
4.4 角的比较
学习目标
1.经历比较角的大小的研究过程,体会角的比较和线段的比较方法的一致性.
2.会比较角的大小,能估计一个角的大小.
3.在操作活动中认识角的平分线,能画出一个角的平分线.
温故知新
1、角是怎样定义的?
定义1:由两条具有公共端点的射线所组成的图形叫角.
定义2:一条射线绕它的端点旋转所组成的图形叫角.
2、怎样来表示一个角?
表示方法(1):用三个大写字母表示;∠AOB
表示方法(2):用一个大写字母表示;∠A
表示方法(3):用一个阿拉伯数字表示;∠1
表示方法(4):用一个希腊字母表示;∠β
每种方法应注意什么问题?
温故知新
3、角是如何分类的
按角的大小可分为:直角、锐角、钝角、平角、周角
4、如何度量一个角?角的单位是什么?如何换算?
可用量角器度量一个角.角的单位是度、分、秒. 1度=60分 1分=60秒
5.线段长短的比较
叠合法、度量法
AB=BC+AC
BC=AB-AC
AC=AB-BC
线段的和、差
线段中点
若点 C 是线段 AB 的中点,则
AC = BC;
AC = BC = AB;
AB = 2 AC = 2 BC.
6.线段的计算
问题探究
知识点一:角的大小比较方法
(1)度量法:用量角器量出角的________, 根据度数比较大小.
∠1=30°,∠2=60°,∠1<∠2
度数
问题:
我们知道角是可以度量的,也就是说角是有大小的,你认为角的大小与什么有关?如何比较角的大小?
(2)叠合法:在比较两个角的大小时,可以将一个角放在另一个角上,使它们的________重合,________重合,看另一边的位置来比较大小(两个角的另一边在重合边的同一侧).
顶点
一边
∠ABC<∠DEF
A
B
C
D
E
F
D
E
F
A
B
C
D
E
F
A
B
C
∠ABC>∠DEF
∠ABC=∠DEF
角的大小指角的两边所张开的角的度数,与角的边的“长”“短”无关!
角既然有大小,那么它就有和、差、倍、分的关系!
注意下面的符号语言:
∠AOB=∠AOC+∠BOC
∠AOC=∠AOB-∠BOC
∠BOC=∠AOB-∠AOC
C
B
O
A
知识要点
在一张纸上画一个角∠AOB, 把纸对折,让角的两边OA与OB重合, 展开后沿折痕画一条射线, 这条射线把这个角分成两部分,这两部分角的大小一样吗?
角平分线定义:
C
B
O
A
从一个角的顶点引出的一条射线,
把这个角分成两个相等的角,这条射
线叫这个角的平分线.
几何语言:
∵OC平分∠AOB,
∴∠AOC=∠BOC
问题探究
例 如图,∠AOB=120°,OD平分∠BOC,OE平分∠AOC.
(1)求∠EOD的度数;
(2)若∠BOC=90°,求∠AOE的度数.
解:(1)∵∠AOB=120°,OD平分∠BOC,OE平分∠AOC,
∴∠EOD=∠DOC+∠EOC=(∠BOC+∠AOC)=∠AOB=×120°=60°.
(2) ∵ ∠AOB=120°,∠BOC=90°,
∴∠AOC=120°-90°=30°,
∵ OE平分∠AOC,
∴∠AOE=∠AOC=×30°=15°.
典例解析
1.下列说法中,正确的是( )
A.角的平分线就是把一个角分成两个角的射线
B.若∠AOB=∠AOC,则OA是∠AOC的平分线
C.角的大小与它的边的长短无关
D.∠CAD与∠BAC的和一定是∠BAD
C
课堂演练
2.如图1,O为直线AB上一点,OD平分∠BOC,若∠BOC=60°,则∠COD的大小为( )
A.120° B.30° C.60° D.150°
B
3.如图2,已知O是直线AB上一点,∠1=40°,OD平分∠BOC,则∠2的度数是________.
70°
4.如图,借助一副三角尺可以画出15°和75°的角,你还能画出哪些度数的角?
75°
15°
15°, 30°, 45°, 60°, 75°, 90°, 105°, 120°, 135°, 150°, 165°.
5.把一副三角尺按如图所示方式拼在一起.
(1)写出∠A,∠B,∠BCD,∠D,∠AED的度数;
(2)用“<”将上述各角连接起来.
解:(1)∠A=30°,∠B=90°,∠BCD=150°,∠D=45°,∠AED=135°.
(2)∠A<∠D<∠B<∠AED<∠BCD.
6.如图,OB是∠AOC的平分线,OD是∠COE的平分线,如果∠AOB=40°,∠COE=60°,那么∠BOD的度数是_____.
70°
7.如图,OC是∠AOB的平分线,∠BOD=∠DOC,∠BOD=10°,则∠AOD的度数为( )
A.50° B.60° C.70° D.80°
C
解:∵点O在直线AB上,
∴∠AOB=∠AOC+∠BOC=180°.
∵ ∠AOC=130°,
∴∠BOC=50°.
∵ OB平分∠COD,所以∠COD=2∠COB=100°.
∴∠AOD=360°-∠AOC-∠COD=360°-130°100°=130°.
∵ OE平分∠AOD,
∴∠AOE=∠AOD=65°.
8.如图,点O是直线AB上的一点,∠AOC=130°,OB平分∠COD,OE平分∠AOD,求∠AOE的度数.
角的大小比较
度量法、叠合法
角的和差
角的平分线
图形语言、文字语言、符号语言
方 法
作 法
描 述
课堂小结
同课章节目录
- 第一章 丰富的图形世界
- 1.1 生活中的立体图形
- 1.2 展开与折叠
- 1.3 截一个几何体
- 1.4 从三个不同方向看物体的形状
- 第二章 有理数及其运算
- 2.1 有理数
- 2.2 数轴
- 2.3 绝对值
- 2.4 有理数的加法
- 2.5 有理数的减法
- 2.6 有理数的加减混合运算
- 2.7 有理数的乘法
- 2.8 有理数的除法
- 2.9 有理数的乘方
- 2.10 科学记数法
- 2.11 有理数的混合运算
- 2.12 用计算器进行运算
- 第三章 整式及其加减
- 3.1 字母表示数
- 3.2 代数式
- 3.3 整式
- 3.4 整式的加减
- 3.5 探索与表达规律
- 第四章 基本平面图形
- 4.1 线段、射线、直线
- 4.2 比较线段的长短
- 4.3 角
- 4.4 角的比较
- 4.5 多边形和圆的初步认识
- 第五章 一元一次方程
- 5.1 认识一元一次方程
- 5.2 求解一元一次方程
- 5.3 应用一元一次方程——水箱变高了
- 5.4 应用一元一次方程——打折销售
- 5.5 应用一元一次方程——“希望工程”义演
- 5.6 应用一元一次方程——追赶小明
- 第六章 数据的收集与整理
- 6.1 数据的收集
- 6.2 普查和抽样调查
- 6.3 数据的表示
- 6.4 统计图的选择
