初数冀教版七上1.10 有理数的乘方 课件(共17张PPT)
文档属性
| 名称 | 初数冀教版七上1.10 有理数的乘方 课件(共17张PPT) |

|
|
| 格式 | pptx | ||
| 文件大小 | 243.8KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 冀教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-09-12 20:17:35 | ||
图片预览




文档简介
(共17张PPT)
1.10 有理数的乘方
1.明白乘方的意义,会进行有理数的乘方运算.
2.经历探索幂的符号法则的过程,会判断幂的符号.
【学习目标】
某种细胞每过30分钟便由1个分裂成2个.请问3小时后1个细胞可以分裂成多少个细胞?
我们知道,1 m=10 dm,1 dm=10 cm,1 cm=10 mm.
则1 m=10 dm=_________cm=________________mm .
10×10
10×10×10
在这里,10×10,10×10×10都是相同因数相乘,为方便起见,我们把10×10记作102,读作10的二次方(或10的平方);把10×10×10记作103,读作10的三次方(或10的立方).
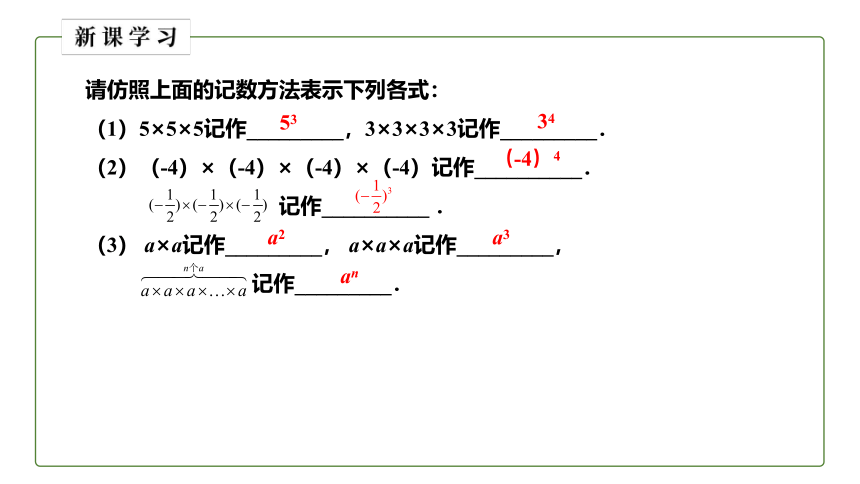
请仿照上面的记数方法表示下列各式:
(1)5×5×5记作_________,3×3×3×3记作_________.
(2)(-4)×(-4)×(-4)×(-4)记作__________.
记作__________ .
(3) a×a记作_________, a×a×a记作_________,
记作_________.
53
34
(-4)4
a2
a3
an
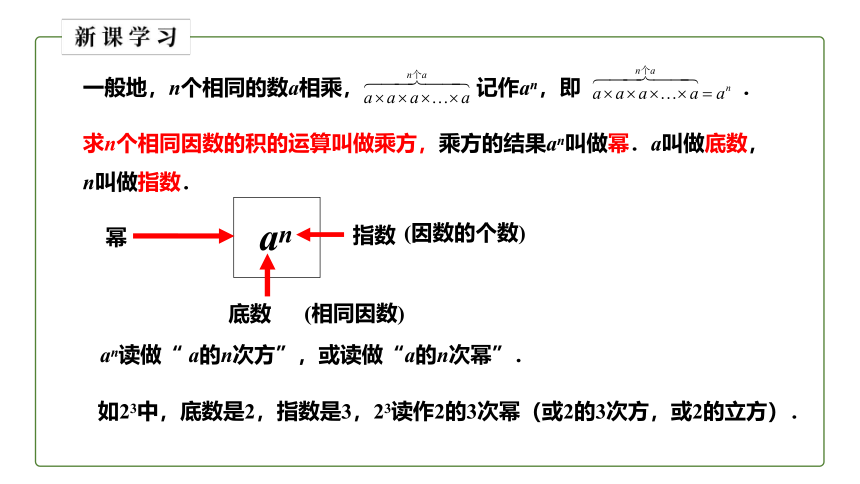
一般地,n个相同的数a相乘, 记作an,即 .
求n个相同因数的积的运算叫做乘方,乘方的结果an叫做幂.a叫做底数,n叫做指数.
an
幂
指数
(因数的个数)
底数
(相同因数)
an读做“ a的n次方”,或读做“a的n次幂”.
如23中,底数是2,指数是3,23读作2的3次幂(或2的3次方,或2的立方).
读一读下列各式,并指出幂的底数和指数:
53,34,(-4)4, ,a2,a3 .
一个数可以看做这个数本身的一次方,举例说明怎样表示一个数的一次方?
例5就是51,通常指数为1时可以省略不写.
例 计算:
(1)(-2)3; (2) ; (3)-26.
解:(1)(-2)3=(-2)×(-2)×(-2);
(2) ;
(3)-26=-2×2×2×2×2×2=-64.
(1)说一说怎样进行有理数的乘方运算?
先根据乘方的意义将乘方转化为乘法,再计算.
(2)-26的底数是多少?它与(-2)6表示的意义相同吗?
-26的底数是2;它表示6个2的乘积的相反数,而(-2)6表示6个-2的乘积,所以它们表示的意义不同.
底数 指数 意义
-an
(-a)n
a
-a
n
n
n个a的乘积的相反数
n个-a的乘积
设n为正整数,
(-1) 5= ________
-1
(-1)4= ________
(-1) 3= ________
(-1) 6= ________
-1
-1
1
(-1) 1= ________
(-1) 2= ________
结论:-1的奇次幂都是-1,-1的偶次幂都是1.
1
1
计算,填表:
(-2)1 (-2)2 (-2)3 (-2)4 (-2)5 (-2)6 …
…
-2
4
-8
16
-32
64
上表中计算结果的符号有什么规律?
当指数是奇数时,幂为负;当指数是偶数时,幂为正.
正数的任何次幂都是正数;负数的奇次幂是负数,负数的偶次幂是正数,0的任何正整数次幂都为0.
计算:
(1) 102 (2)(-10)2
103 (-10)3
104 (-10)4
=100
=1 000
=10 000
=100
=-1 000
=10 000
观察上面的计算的结果,你能发现什么规律?
1、10的几次幂,1的后面就有几个0.
2、互为相反数的相同偶次幂相等,相同奇次幂互为相反数.
1. 45 表示 ( )
A . 4个5相乘 B . 5个4相乘
C . 5与4的积 D. 5个4相加的和
2.计算(-1)3的值等于( )
A.-1 B.1 C.-2 D.2
3.对于乘积(-3)×(-3)×(-3)×(-3),记法正确的是( )
A.-34 B.-(+3)4 C.(-3)4 D.(-3)×4
4.计算-24=( )
A.8 B.-8 C.16 D.-16
B
A
C
D
5.计算:
(1) ; (2)(-1)2021; (3)-(-2)4.
解:(1) ;
(2)(-1)2021=-1;
(3)-(-2)4= - (-2)×(-2)×(-2)×(-2)= -16;
6.某种细胞每过30分钟便由1个分裂成2个.请问3小时后1个细胞可以分裂成多少个细胞?
解:根据题意,第一次可以分裂出21=2,
第二次可以分裂出22=4,
第三次可以分裂出23=8,…,
∵3小时里有6个30分钟,
26=64,
∴3小时后可以分裂出64个细胞.
1.有理数的乘方:求n个相同因数的积的运算叫做乘方,乘方的结果an叫做幂.
a叫做底数,n叫做指数.
2.幂的符号法则:
正数的任何次幂都是正数;负数的奇次幂是负数,负数的偶次幂是正数.
0的任何正整数次幂都为0.
教材第48页A组1题,3题.
完成配套课后练习.
1.10 有理数的乘方
1.明白乘方的意义,会进行有理数的乘方运算.
2.经历探索幂的符号法则的过程,会判断幂的符号.
【学习目标】
某种细胞每过30分钟便由1个分裂成2个.请问3小时后1个细胞可以分裂成多少个细胞?
我们知道,1 m=10 dm,1 dm=10 cm,1 cm=10 mm.
则1 m=10 dm=_________cm=________________mm .
10×10
10×10×10
在这里,10×10,10×10×10都是相同因数相乘,为方便起见,我们把10×10记作102,读作10的二次方(或10的平方);把10×10×10记作103,读作10的三次方(或10的立方).
请仿照上面的记数方法表示下列各式:
(1)5×5×5记作_________,3×3×3×3记作_________.
(2)(-4)×(-4)×(-4)×(-4)记作__________.
记作__________ .
(3) a×a记作_________, a×a×a记作_________,
记作_________.
53
34
(-4)4
a2
a3
an
一般地,n个相同的数a相乘, 记作an,即 .
求n个相同因数的积的运算叫做乘方,乘方的结果an叫做幂.a叫做底数,n叫做指数.
an
幂
指数
(因数的个数)
底数
(相同因数)
an读做“ a的n次方”,或读做“a的n次幂”.
如23中,底数是2,指数是3,23读作2的3次幂(或2的3次方,或2的立方).
读一读下列各式,并指出幂的底数和指数:
53,34,(-4)4, ,a2,a3 .
一个数可以看做这个数本身的一次方,举例说明怎样表示一个数的一次方?
例5就是51,通常指数为1时可以省略不写.
例 计算:
(1)(-2)3; (2) ; (3)-26.
解:(1)(-2)3=(-2)×(-2)×(-2);
(2) ;
(3)-26=-2×2×2×2×2×2=-64.
(1)说一说怎样进行有理数的乘方运算?
先根据乘方的意义将乘方转化为乘法,再计算.
(2)-26的底数是多少?它与(-2)6表示的意义相同吗?
-26的底数是2;它表示6个2的乘积的相反数,而(-2)6表示6个-2的乘积,所以它们表示的意义不同.
底数 指数 意义
-an
(-a)n
a
-a
n
n
n个a的乘积的相反数
n个-a的乘积
设n为正整数,
(-1) 5= ________
-1
(-1)4= ________
(-1) 3= ________
(-1) 6= ________
-1
-1
1
(-1) 1= ________
(-1) 2= ________
结论:-1的奇次幂都是-1,-1的偶次幂都是1.
1
1
计算,填表:
(-2)1 (-2)2 (-2)3 (-2)4 (-2)5 (-2)6 …
…
-2
4
-8
16
-32
64
上表中计算结果的符号有什么规律?
当指数是奇数时,幂为负;当指数是偶数时,幂为正.
正数的任何次幂都是正数;负数的奇次幂是负数,负数的偶次幂是正数,0的任何正整数次幂都为0.
计算:
(1) 102 (2)(-10)2
103 (-10)3
104 (-10)4
=100
=1 000
=10 000
=100
=-1 000
=10 000
观察上面的计算的结果,你能发现什么规律?
1、10的几次幂,1的后面就有几个0.
2、互为相反数的相同偶次幂相等,相同奇次幂互为相反数.
1. 45 表示 ( )
A . 4个5相乘 B . 5个4相乘
C . 5与4的积 D. 5个4相加的和
2.计算(-1)3的值等于( )
A.-1 B.1 C.-2 D.2
3.对于乘积(-3)×(-3)×(-3)×(-3),记法正确的是( )
A.-34 B.-(+3)4 C.(-3)4 D.(-3)×4
4.计算-24=( )
A.8 B.-8 C.16 D.-16
B
A
C
D
5.计算:
(1) ; (2)(-1)2021; (3)-(-2)4.
解:(1) ;
(2)(-1)2021=-1;
(3)-(-2)4= - (-2)×(-2)×(-2)×(-2)= -16;
6.某种细胞每过30分钟便由1个分裂成2个.请问3小时后1个细胞可以分裂成多少个细胞?
解:根据题意,第一次可以分裂出21=2,
第二次可以分裂出22=4,
第三次可以分裂出23=8,…,
∵3小时里有6个30分钟,
26=64,
∴3小时后可以分裂出64个细胞.
1.有理数的乘方:求n个相同因数的积的运算叫做乘方,乘方的结果an叫做幂.
a叫做底数,n叫做指数.
2.幂的符号法则:
正数的任何次幂都是正数;负数的奇次幂是负数,负数的偶次幂是正数.
0的任何正整数次幂都为0.
教材第48页A组1题,3题.
完成配套课后练习.
同课章节目录
- 第一章 有理数
- 1.1 正数和负数
- 1.2 数轴
- 1.3 绝对值与相反数
- 1.4 有理数的大小
- 1.5 有理数的加法
- 1.6 有理数的减法
- 1.7 有理数的加减混合运算
- 1.8 有理数的乘法
- 1.9 有理数的除法
- 1.10 有理数的乘方
- 1.11 有理数的混合运算
- 1.12 计算器的使用
- 第二章 几何图形的初步认识
- 2.1 从生活中认识几何图形
- 2.2 点和线
- 2.3 线段长短的比较
- 2.4 线段的和与差
- 2.5 角以及角的度量
- 2.6 角的大小
- 2.7 角的和与差
- 2.8 平面图形的旋转
- 第三章 代数式
- 3.1 用字母表示数
- 3.2 代数式
- 3.3 代数式的值
- 第四章 整式的加减
- 4.1 整式
- 4.2 合并同类项
- 4.3 去括号
- 4.4 整式的加减
- 第五章 一元一次方程
- 5.1一元一次方程
- 5.2 等式的基本性质
- 5.3 解一元一次方程
- 5.4 一元一次方程的应用
