初中数学人教版八上15.2.2分式加减(1) 课件(共23张PPT)
文档属性
| 名称 | 初中数学人教版八上15.2.2分式加减(1) 课件(共23张PPT) |

|
|
| 格式 | pptx | ||
| 文件大小 | 1.6MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-09-12 20:26:09 | ||
图片预览








文档简介
(共23张PPT)
15.2.2 分式加减1
1.理解掌握异分母分式加减法法则;能正确熟练地进行同分母分式加减和异分母分式的加减运算.
2.在课堂活动中培养学生乐于探究、合作学习的习惯,渗透类比、化归数学思想方法.
3.在合作探究的过程中,激发学生学习数学的兴趣,重视在学习过程中对学生的数学能力培养,渗透类比转化的数学思想方法.
甲工程队完成一项工程需n 天,乙工程队要比甲队多用3天才能完成这项工程,两队共同工作一天完成这项工程的几分之几?
分析:
(1)甲工程队一天完成这项工程的几分之几?
(2)乙工程队一天完成这项工程的几分之几?
(3)甲乙两队共同工作一天完成这项工程的几分之几?
解决问题:
(1)甲工程队一天完成这项工程的
(2)乙工程队一天完成这项工程的;
(3)甲乙两队共同工作一天完成这项工程的.
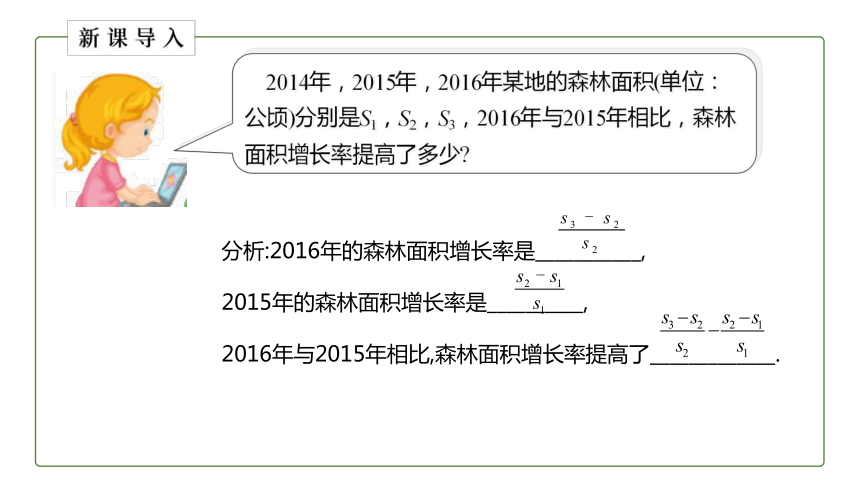
2014年,2015年,2016年某地的森林面积(单位:公顷)分别是S1,S2,S3,2016年与2015年相比,森林面积增长率提高了多少
分析:2016年的森林面积增长率是___________,
2015年的森林面积增长率是__________,
2016年与2015年相比,森林面积增长率提高了_____________.
探究
2.你认为:
1.同分母分数加减法的法则如何叙述?
同分母分数相加减,分母不变,把分子相加减.
计算:
猜想:
结论
同分母分式相加减,分母不变,把分子相加减
上述法则可用式子表示为
同分母分式的加减法则
解:原式=
=
=
=
例1:计算.
解:原式=
=
=
=
(1)注意分数线有括号的作用,分子相加减时,要注意添括号.
(2)把分子相加减后,如果所得结果不是最简分式,要约分.
归纳
问题:
请计 ( ), ( ).
异分母分数相加减
分数的通分
依据:分数的基本性质
转化
同分母分数相加减
异分母分数相加减,先通分,
变为同分母的分数,再加减 .
探究
依据:分数基本性质
分数的通分
同分母分数相加减
异分母分数相加减
转化
异分母分数相加减,先通分,变为同分母的分数,再加减.
异分母分式相加减
分式的通分
依据:分式基本性质
转化
同分母分式相加减
异分母分式相加减,先通分,变为同分母的分式,再加减.
类比:异分母的分式应该如何加减
探究
异分母分式的加减法则
异分母分式相加减,先通分,变同分母的分式,再加减.
上述法则可用式子表示为
结论
指出下列各式的最简公分母.
解:原式=
=
=
例2:计算:
解:原式=
解:原式=
=
=
=
分式的加减法的思路
通分
转化为
异分母相加减
同分母
相加减
分子(整式)相加减
分母不变
转化为
问题1:甲乙两队共同工作一天完成这项工程的:
问题2:2016年与2015年相比,
森林面积增长率提高了:
计算: ,
解:原式
从1、-3、3中任选一个你喜欢的m值代入求值.
当m=1时,原式
例3.计算:
法一:
原式=
法二:
原式=
先化简,再求值:
先化简,再求值: ,其中 .
解:原式=
当x=-4时,原式 .
分式加减运算
加减法运算
注意
(1)减式的分式是多项式时,在进行运算时要适时添加括号;
异分母分式相加减先转化为同分母分式的加减运算
(2)整式和分式之间进行加减运算时,则要把整式看成分母是1的分式,以便通分;
(3)异分母分式进行加减运算需要先通分,关键是确定最简公分母.
完成本节课配套习题.
15.2.2 分式加减1
1.理解掌握异分母分式加减法法则;能正确熟练地进行同分母分式加减和异分母分式的加减运算.
2.在课堂活动中培养学生乐于探究、合作学习的习惯,渗透类比、化归数学思想方法.
3.在合作探究的过程中,激发学生学习数学的兴趣,重视在学习过程中对学生的数学能力培养,渗透类比转化的数学思想方法.
甲工程队完成一项工程需n 天,乙工程队要比甲队多用3天才能完成这项工程,两队共同工作一天完成这项工程的几分之几?
分析:
(1)甲工程队一天完成这项工程的几分之几?
(2)乙工程队一天完成这项工程的几分之几?
(3)甲乙两队共同工作一天完成这项工程的几分之几?
解决问题:
(1)甲工程队一天完成这项工程的
(2)乙工程队一天完成这项工程的;
(3)甲乙两队共同工作一天完成这项工程的.
2014年,2015年,2016年某地的森林面积(单位:公顷)分别是S1,S2,S3,2016年与2015年相比,森林面积增长率提高了多少
分析:2016年的森林面积增长率是___________,
2015年的森林面积增长率是__________,
2016年与2015年相比,森林面积增长率提高了_____________.
探究
2.你认为:
1.同分母分数加减法的法则如何叙述?
同分母分数相加减,分母不变,把分子相加减.
计算:
猜想:
结论
同分母分式相加减,分母不变,把分子相加减
上述法则可用式子表示为
同分母分式的加减法则
解:原式=
=
=
=
例1:计算.
解:原式=
=
=
=
(1)注意分数线有括号的作用,分子相加减时,要注意添括号.
(2)把分子相加减后,如果所得结果不是最简分式,要约分.
归纳
问题:
请计 ( ), ( ).
异分母分数相加减
分数的通分
依据:分数的基本性质
转化
同分母分数相加减
异分母分数相加减,先通分,
变为同分母的分数,再加减 .
探究
依据:分数基本性质
分数的通分
同分母分数相加减
异分母分数相加减
转化
异分母分数相加减,先通分,变为同分母的分数,再加减.
异分母分式相加减
分式的通分
依据:分式基本性质
转化
同分母分式相加减
异分母分式相加减,先通分,变为同分母的分式,再加减.
类比:异分母的分式应该如何加减
探究
异分母分式的加减法则
异分母分式相加减,先通分,变同分母的分式,再加减.
上述法则可用式子表示为
结论
指出下列各式的最简公分母.
解:原式=
=
=
例2:计算:
解:原式=
解:原式=
=
=
=
分式的加减法的思路
通分
转化为
异分母相加减
同分母
相加减
分子(整式)相加减
分母不变
转化为
问题1:甲乙两队共同工作一天完成这项工程的:
问题2:2016年与2015年相比,
森林面积增长率提高了:
计算: ,
解:原式
从1、-3、3中任选一个你喜欢的m值代入求值.
当m=1时,原式
例3.计算:
法一:
原式=
法二:
原式=
先化简,再求值:
先化简,再求值: ,其中 .
解:原式=
当x=-4时,原式 .
分式加减运算
加减法运算
注意
(1)减式的分式是多项式时,在进行运算时要适时添加括号;
异分母分式相加减先转化为同分母分式的加减运算
(2)整式和分式之间进行加减运算时,则要把整式看成分母是1的分式,以便通分;
(3)异分母分式进行加减运算需要先通分,关键是确定最简公分母.
完成本节课配套习题.
