初中数学人教版八下16.3.1二次根式的加减 教案
文档属性
| 名称 | 初中数学人教版八下16.3.1二次根式的加减 教案 |

|
|
| 格式 | docx | ||
| 文件大小 | 309.5KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-09-12 00:00:00 | ||
图片预览


文档简介
16.3.1二次根式的加减
教学内容分析
在二次根式性质和乘除运算的基础上,本节课进一步学习二次根式的加减运算.前几节课学习的二次根式的乘除法法则都是为二次根式的化简做准备的,而最简二次根式又是加减运算的基础.二次根式的运算方法与数的运算方法本质上是一致的,实数的运算律对二次根式的运算仍然适用. 与分式的运算类似,二次根式的乘除运算比加减运算简单.二次根式乘除运算可直接利用运算法则,而二次根式加减运算则要先化简,再合并“同类项”. 二次根式加减运算的基本依据是二次根式的性质和分配律.
教学目标
1.了解二次根式的加、减运算法则;
2.会用二次根式的加、减运算法则进行简单的运算.
教学重难点
【重点】应用分配律进行二次根式的加减运算.
【难点】会用二次根式的加、减运算法则进行简单的运算.
教学方法
问题启发法、观察归纳法、探究法
教学过程
(一)复习导入
多媒体出示问题:
问题1 满足什么条件的根式是最简二次根式?
(1)被开方数不含分母;
(2)被开方数中不含能开得尽方的因数或因式.
问题2 化简下列两组二次根式,每组化简后有什么共同特点?
(1); (2)
问题3 有八只小白兔,每只身上都标有一个最简二次根式,你能根据被开方数的特征将这些小白兔分到四个不同的栅栏里吗?
意图:复习最简二次根式的内容,为本节课找同类二次根式奠定知识基础,之后通过观察和归类引出本节的同类二次根式.
效果:运用复习和归类的一系列问题引发学生思考,引出课题.
新课讲授
同类二次根式
在七年级我们就已经学过单项式加单项式的法则.观察下图并思考.
前面依次往下推导,由特殊到一般易知二次根式的被开方数相同可以合并.继续观察下面的过程:
你又有什么发现吗?
归纳总结:将二次根式化成最简式,如果被开方数相同,则这样的二次根式可以合并.我们称可以合并的二次根式为同类二次根式.
注意:判断几个二次根式是否可以合并,一定都要化为最简二次根式再判断.
合并的方法与合并同类项类似,把根号外的因数(式)相加,根指数和被开方数(式)不变.如:
意图:通过复习旧知,类比同类项的概念,归纳出同类二次根式的概念,为二次根式的加减法则的探究做准备.
效果:学生在教师的引导下,类比得出了同类二次根式的概念.
例1 若最简根式与可以合并,求的值.
解:由题意得,解得,即
归纳: 确定可以合并的二次根式中字母取值的方法:利用被开方数相同,指数都为2,列关于待定字母的方程求解即可.
练一练 (1)下列各式中,与是同类二次根式的是( D )
B. C. D.
(2)与最简二次根式能合并,则m=1.
(3)下列二次根式,不能与合并的是②⑤(填序号).
①;②;③;④;⑤.
意图:通过例题和练习,让学生更加明白了如何辨别同类二次根式,以及必须先化为最简二次根式的注意事项.
效果:学生在运用中加深了对同类二次根式的理解.
二次根式的加减及其应用
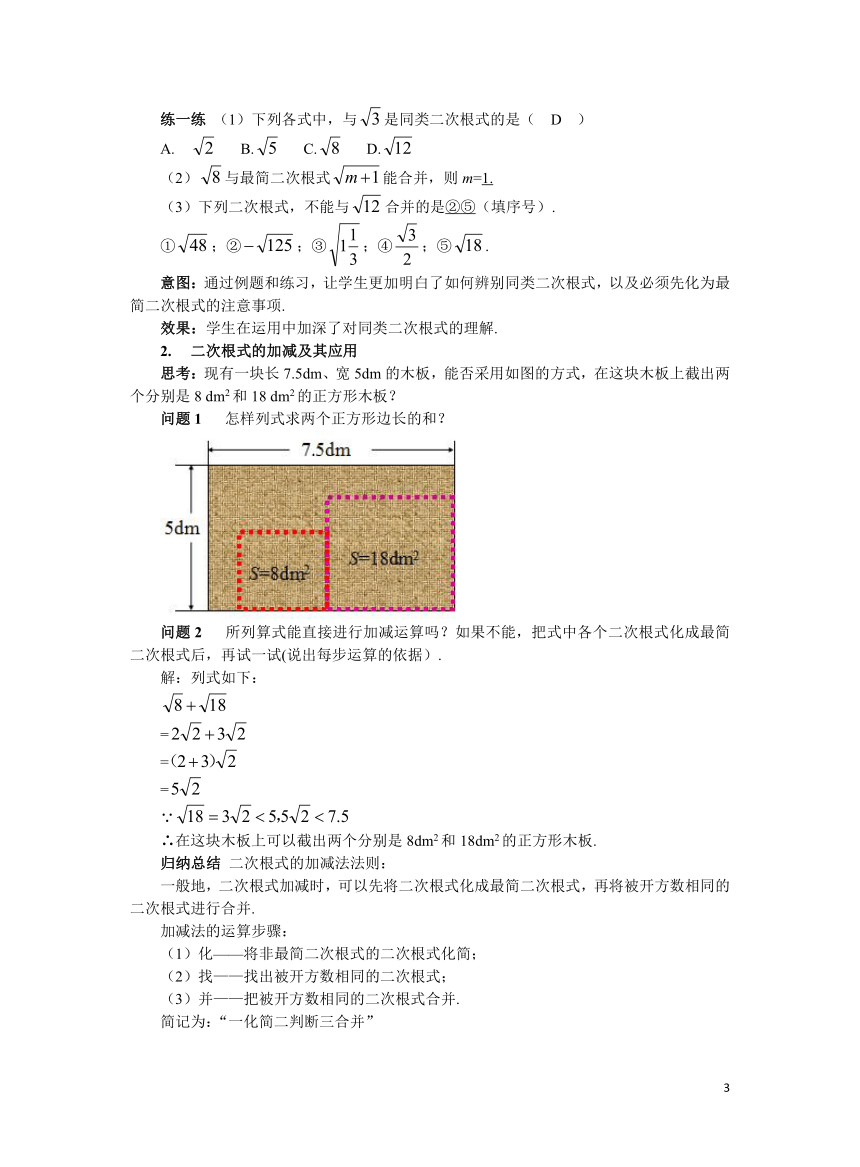
思考:现有一块长7.5dm、宽5dm的木板,能否采用如图的方式,在这块木板上截出两个分别是8 dm2和18 dm2的正方形木板?
问题1 怎样列式求两个正方形边长的和?
问题2 所列算式能直接进行加减运算吗?如果不能,把式中各个二次根式化成最简二次根式后,再试一试(说出每步运算的依据).
解:列式如下:
=
=
=
∴在这块木板上可以截出两个分别是8dm2和18dm2的正方形木板.
归纳总结 二次根式的加减法法则:
一般地,二次根式加减时,可以先将二次根式化成最简二次根式,再将被开方数相同的二次根式进行合并.
加减法的运算步骤:
(1)化——将非最简二次根式的二次根式化简;
(2)找——找出被开方数相同的二次根式;
(3)并——把被开方数相同的二次根式合并.
简记为:“一化简二判断三合并”
依据:二次根式的性质、分配律和整式加减法则.
基本思想:把二次根式加减问题转化为整式加减问题.
意图:学生类比整式加减中的合并同类项,探究出了二次根式的加减法则,并归纳计算步骤,将法则程序化、可操作化.同时还将二次根式的加减法则和分配律的运算法则相联系,让学生更明白其中的算理.
效果:学生通过类比探究,得出了二次根式的加减法则和计算步骤.
例2 计算:
;
(2);
;
例3 计算:
;
练一练
下列计算正确的是 ( C )
B.
C. D.
(2)已知一个矩形的长为,宽为,则其周长为______.
意图:设计不同类型的计算题,让学生在练习中体会二次根式加减法的计算过程.
效果:学生通过练习基本掌握了二次根式加减法的运算.
(三)课堂练习
1.二次根式:中,与能进行合并的是(C)
A. B. C. D.
2.下列运算中错误的是(A)
A.
B.
C.
D.
3.三角形的三边长分别为则这个三角形的周长为__________.
4.计算:
(1)
(2)
(3)
(4)
5.计算:
(1);(2)
(3);(4)
意图:检测学生对二次根式的加减法法则、可以合并的同类二次根式的运用、掌握情况.
效果:巩固了学生对二次根式的加减法法则、同类二次根式的运用.
(四)课堂小结
先让学生自己总结反思,然后同学之间进行交流,再找学生谈谈自己的收获.
同类二次根式:
将二次根式化成最简式,如果被开方数相同,则这样的二次根式可以合并.我们称可以合并的二次根式为同类二次根式.
二次根式的加减法则
(1)化——将非最简二次根式的二次根式化简;
(2)找——找出被开方数相同的二次根式;
(3)并——把被开方数相同的二次根式合并.
简记为:“一化简二判断三合并”
意图:总结反思是一节课必不可少的环节,有助于学生巩固所学知识和技能.
效果:学生对本节课所学知识有了系统的回顾.
(五)作业布置
完成配套练习
板书设计
16.3.1二次根式的加减
1.同类二次根式:
将二次根式化成最简式,如果被开方数相同,则这样的二次根式可以合并.我们称可以合并的二次根式为同类二次根式.
2.二次根式的加减法则
(1)化——将非最简二次根式的二次根式化简;
(2)找——找出被开方数相同的二次根式;
(3)并——把被开方数相同的二次根式合并.
简记为:“一化简二判断三合并”
课后反思
本节课二次根式的加减和之前学过的整式的加减有类似的地方,因此让学生回忆合并同类项的知识,进而归纳出同类二次根式,在探究过程中,充分发挥学生在学习中的主体性地位,让学生经历计算、观察、总结、归纳、练习运用的数学研究过程,体会数学中的算理,培养学生的数感,提高学生的计算能力.辨别同类二次根式的前提是化为最简二次根式,看被开方数是否相同.找到同类二次根式是进行二次根式加减运算时的重要步骤,对学生的计算有重要的意义,因此在本节课中有意让学生类比合并同类项,自己探究出二次根式加减法法则和步骤.本节课的不足之处是:注重探究和计算,忽略了二次根式加减法在实际问题中的运用,在课后的练习题目中还需要针对此知识点进行实际运用练习.
1
教学内容分析
在二次根式性质和乘除运算的基础上,本节课进一步学习二次根式的加减运算.前几节课学习的二次根式的乘除法法则都是为二次根式的化简做准备的,而最简二次根式又是加减运算的基础.二次根式的运算方法与数的运算方法本质上是一致的,实数的运算律对二次根式的运算仍然适用. 与分式的运算类似,二次根式的乘除运算比加减运算简单.二次根式乘除运算可直接利用运算法则,而二次根式加减运算则要先化简,再合并“同类项”. 二次根式加减运算的基本依据是二次根式的性质和分配律.
教学目标
1.了解二次根式的加、减运算法则;
2.会用二次根式的加、减运算法则进行简单的运算.
教学重难点
【重点】应用分配律进行二次根式的加减运算.
【难点】会用二次根式的加、减运算法则进行简单的运算.
教学方法
问题启发法、观察归纳法、探究法
教学过程
(一)复习导入
多媒体出示问题:
问题1 满足什么条件的根式是最简二次根式?
(1)被开方数不含分母;
(2)被开方数中不含能开得尽方的因数或因式.
问题2 化简下列两组二次根式,每组化简后有什么共同特点?
(1); (2)
问题3 有八只小白兔,每只身上都标有一个最简二次根式,你能根据被开方数的特征将这些小白兔分到四个不同的栅栏里吗?
意图:复习最简二次根式的内容,为本节课找同类二次根式奠定知识基础,之后通过观察和归类引出本节的同类二次根式.
效果:运用复习和归类的一系列问题引发学生思考,引出课题.
新课讲授
同类二次根式
在七年级我们就已经学过单项式加单项式的法则.观察下图并思考.
前面依次往下推导,由特殊到一般易知二次根式的被开方数相同可以合并.继续观察下面的过程:
你又有什么发现吗?
归纳总结:将二次根式化成最简式,如果被开方数相同,则这样的二次根式可以合并.我们称可以合并的二次根式为同类二次根式.
注意:判断几个二次根式是否可以合并,一定都要化为最简二次根式再判断.
合并的方法与合并同类项类似,把根号外的因数(式)相加,根指数和被开方数(式)不变.如:
意图:通过复习旧知,类比同类项的概念,归纳出同类二次根式的概念,为二次根式的加减法则的探究做准备.
效果:学生在教师的引导下,类比得出了同类二次根式的概念.
例1 若最简根式与可以合并,求的值.
解:由题意得,解得,即
归纳: 确定可以合并的二次根式中字母取值的方法:利用被开方数相同,指数都为2,列关于待定字母的方程求解即可.
练一练 (1)下列各式中,与是同类二次根式的是( D )
B. C. D.
(2)与最简二次根式能合并,则m=1.
(3)下列二次根式,不能与合并的是②⑤(填序号).
①;②;③;④;⑤.
意图:通过例题和练习,让学生更加明白了如何辨别同类二次根式,以及必须先化为最简二次根式的注意事项.
效果:学生在运用中加深了对同类二次根式的理解.
二次根式的加减及其应用
思考:现有一块长7.5dm、宽5dm的木板,能否采用如图的方式,在这块木板上截出两个分别是8 dm2和18 dm2的正方形木板?
问题1 怎样列式求两个正方形边长的和?
问题2 所列算式能直接进行加减运算吗?如果不能,把式中各个二次根式化成最简二次根式后,再试一试(说出每步运算的依据).
解:列式如下:
=
=
=
∴在这块木板上可以截出两个分别是8dm2和18dm2的正方形木板.
归纳总结 二次根式的加减法法则:
一般地,二次根式加减时,可以先将二次根式化成最简二次根式,再将被开方数相同的二次根式进行合并.
加减法的运算步骤:
(1)化——将非最简二次根式的二次根式化简;
(2)找——找出被开方数相同的二次根式;
(3)并——把被开方数相同的二次根式合并.
简记为:“一化简二判断三合并”
依据:二次根式的性质、分配律和整式加减法则.
基本思想:把二次根式加减问题转化为整式加减问题.
意图:学生类比整式加减中的合并同类项,探究出了二次根式的加减法则,并归纳计算步骤,将法则程序化、可操作化.同时还将二次根式的加减法则和分配律的运算法则相联系,让学生更明白其中的算理.
效果:学生通过类比探究,得出了二次根式的加减法则和计算步骤.
例2 计算:
;
(2);
;
例3 计算:
;
练一练
下列计算正确的是 ( C )
B.
C. D.
(2)已知一个矩形的长为,宽为,则其周长为______.
意图:设计不同类型的计算题,让学生在练习中体会二次根式加减法的计算过程.
效果:学生通过练习基本掌握了二次根式加减法的运算.
(三)课堂练习
1.二次根式:中,与能进行合并的是(C)
A. B. C. D.
2.下列运算中错误的是(A)
A.
B.
C.
D.
3.三角形的三边长分别为则这个三角形的周长为__________.
4.计算:
(1)
(2)
(3)
(4)
5.计算:
(1);(2)
(3);(4)
意图:检测学生对二次根式的加减法法则、可以合并的同类二次根式的运用、掌握情况.
效果:巩固了学生对二次根式的加减法法则、同类二次根式的运用.
(四)课堂小结
先让学生自己总结反思,然后同学之间进行交流,再找学生谈谈自己的收获.
同类二次根式:
将二次根式化成最简式,如果被开方数相同,则这样的二次根式可以合并.我们称可以合并的二次根式为同类二次根式.
二次根式的加减法则
(1)化——将非最简二次根式的二次根式化简;
(2)找——找出被开方数相同的二次根式;
(3)并——把被开方数相同的二次根式合并.
简记为:“一化简二判断三合并”
意图:总结反思是一节课必不可少的环节,有助于学生巩固所学知识和技能.
效果:学生对本节课所学知识有了系统的回顾.
(五)作业布置
完成配套练习
板书设计
16.3.1二次根式的加减
1.同类二次根式:
将二次根式化成最简式,如果被开方数相同,则这样的二次根式可以合并.我们称可以合并的二次根式为同类二次根式.
2.二次根式的加减法则
(1)化——将非最简二次根式的二次根式化简;
(2)找——找出被开方数相同的二次根式;
(3)并——把被开方数相同的二次根式合并.
简记为:“一化简二判断三合并”
课后反思
本节课二次根式的加减和之前学过的整式的加减有类似的地方,因此让学生回忆合并同类项的知识,进而归纳出同类二次根式,在探究过程中,充分发挥学生在学习中的主体性地位,让学生经历计算、观察、总结、归纳、练习运用的数学研究过程,体会数学中的算理,培养学生的数感,提高学生的计算能力.辨别同类二次根式的前提是化为最简二次根式,看被开方数是否相同.找到同类二次根式是进行二次根式加减运算时的重要步骤,对学生的计算有重要的意义,因此在本节课中有意让学生类比合并同类项,自己探究出二次根式加减法法则和步骤.本节课的不足之处是:注重探究和计算,忽略了二次根式加减法在实际问题中的运用,在课后的练习题目中还需要针对此知识点进行实际运用练习.
1
