初中数学人教版九下29.2三视图(第3课时) 教案
文档属性
| 名称 | 初中数学人教版九下29.2三视图(第3课时) 教案 |

|
|
| 格式 | doc | ||
| 文件大小 | 292.5KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-09-12 00:00:00 | ||
图片预览

文档简介
29.2三视图
(第3课时)
一、教学内容分析
本章对于“三视图”的学习,从两方面来反映平面图形与立体图形的联系.一是画形状简单的几何体的三视图,由立体图形得到相应平面图形的过程,即“由物画图”;二是由三视图想出相应物体形状的内容,这些是由平面图形得到相应立体图形的过程,即“由图想物”,本课时是在上一课时基础上继续研究“由图想物”,涉及三视图与表面展开图两种不同的立体图形平面化处理方式,研究与三视图有关的计算问题.
二、教学目标
1.会根据三视图想象物体的表面展开图;
2.根据三视图形状和数据进行计算,会确定组成立体图形的小正方体个数.
3.在经历“三视图——实物(几何体)——展开图”的探索过程中,进一步发展几何直观和空间观念,体会转化思想;
三、教学重难点
【重点】探索三视图、实物(几何体)、展开图三者之间的转化关系.
【难点】利用三视图中的数据信息进行计算或计数.
四、教学方法
演示法.由于初中学生的三维空间观念尚未成熟,想象空间中几何元素的位置关系有一定困难,所以在教学中适当利用几何体或者实物模型(比如不同形状的纸盒)进行演示说明,让学生有初步感知,再逐步培养在脑海中想象物体形状、位置和大小关系.
五、教学过程
(一)新课导入
问题1 一个无盖盒子的三视图如图所示,请画出它的实物图,并说出这个盒子长、宽、高的尺寸单位:cm).
【提示】这个盒子的实物图如图所示,长200cm,宽100cm,高50cm.
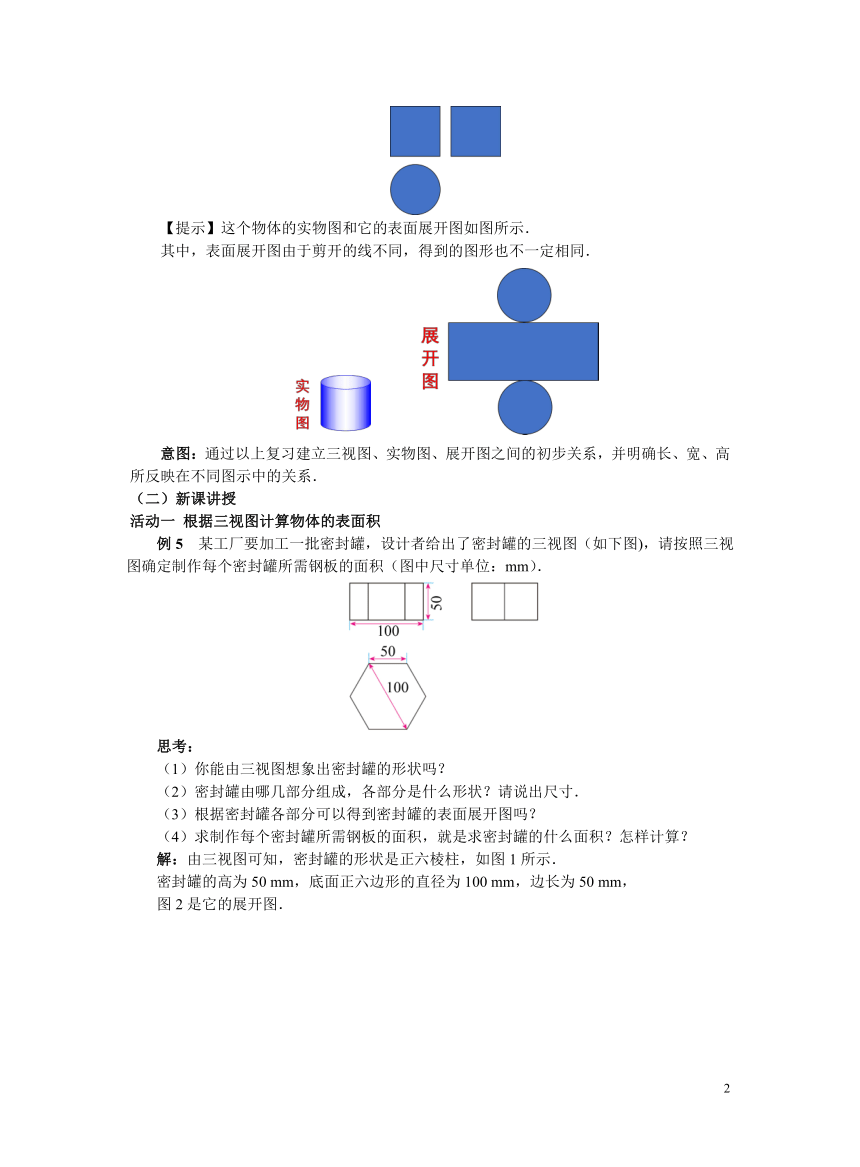
问题2 一个物体的三视图如图所示,请画出这个物体的实物图和它的表面展开图.
【提示】这个物体的实物图和它的表面展开图如图所示.
其中,表面展开图由于剪开的线不同,得到的图形也不一定相同.
意图:通过以上复习建立三视图、实物图、展开图之间的初步关系,并明确长、宽、高所反映在不同图示中的关系.
(二)新课讲授
活动一 根据三视图计算物体的表面积
例5 某工厂要加工一批密封罐,设计者给出了密封罐的三视图(如下图),请按照三视图确定制作每个密封罐所需钢板的面积(图中尺寸单位:mm).
思考:
(1)你能由三视图想象出密封罐的形状吗?
(2)密封罐由哪几部分组成,各部分是什么形状?请说出尺寸.
(3)根据密封罐各部分可以得到密封罐的表面展开图吗?
(4)求制作每个密封罐所需钢板的面积,就是求密封罐的什么面积?怎样计算?
解:由三视图可知,密封罐的形状是正六棱柱,如图1所示.
密封罐的高为50 mm,底面正六边形的直径为100 mm,边长为50 mm,
图2是它的展开图.
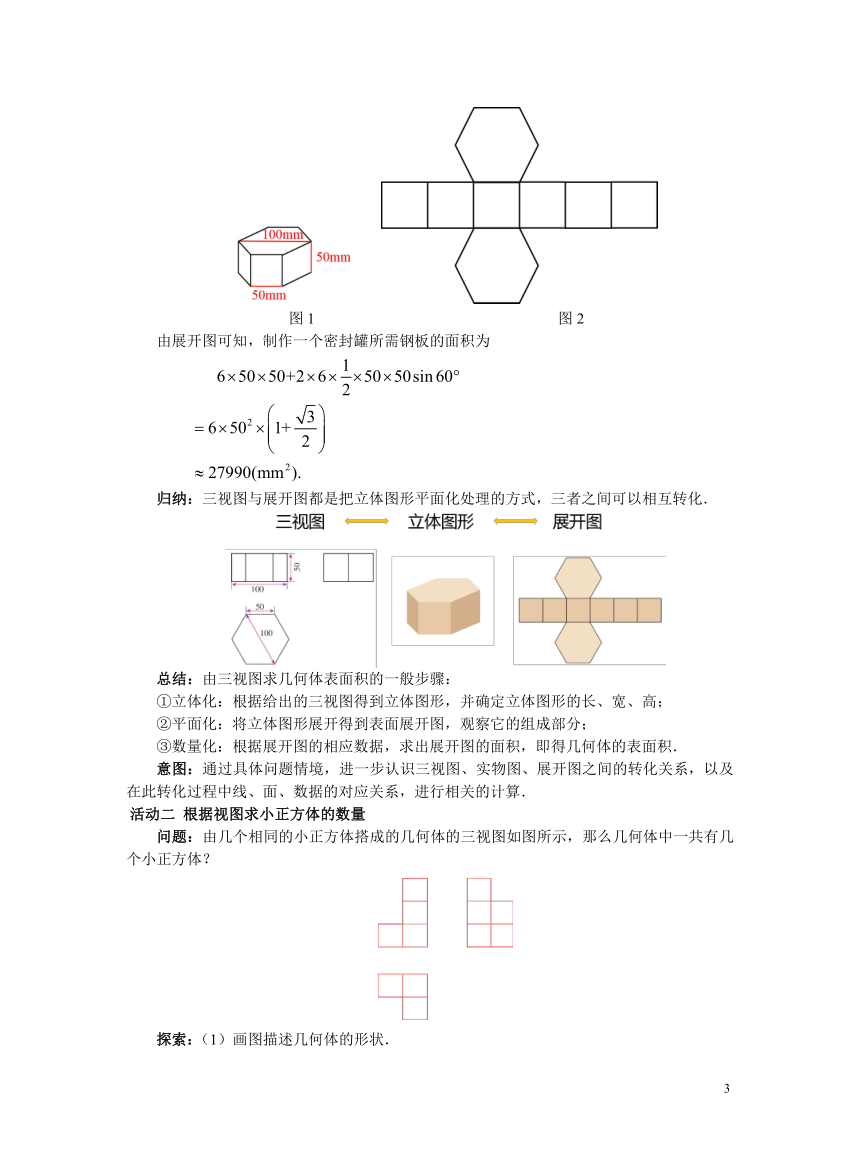
图1 图2
由展开图可知,制作一个密封罐所需钢板的面积为
归纳:三视图与展开图都是把立体图形平面化处理的方式,三者之间可以相互转化.
总结:由三视图求几何体表面积的一般步骤:
①立体化:根据给出的三视图得到立体图形,并确定立体图形的长、宽、高;
②平面化:将立体图形展开得到表面展开图,观察它的组成部分;
③数量化:根据展开图的相应数据,求出展开图的面积,即得几何体的表面积.
意图:通过具体问题情境,进一步认识三视图、实物图、展开图之间的转化关系,以及在此转化过程中线、面、数据的对应关系,进行相关的计算.
活动二 根据视图求小正方体的数量
问题:由几个相同的小正方体搭成的几何体的三视图如图所示,那么几何体中一共有几个小正方体?
探索:(1)画图描述几何体的形状.
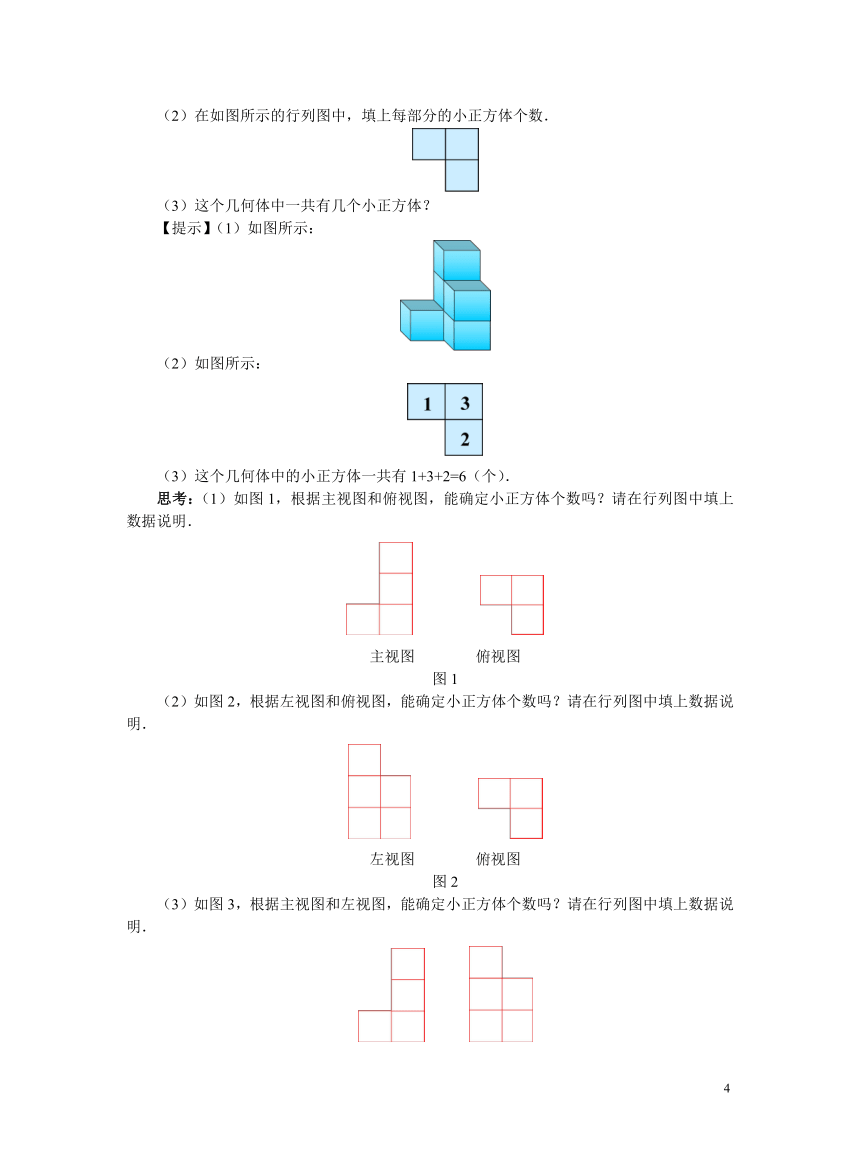
(2)在如图所示的行列图中,填上每部分的小正方体个数.
(3)这个几何体中一共有几个小正方体?
【提示】(1)如图所示:
(2)如图所示:
(3)这个几何体中的小正方体一共有1+3+2=6(个).
思考:(1)如图1,根据主视图和俯视图,能确定小正方体个数吗?请在行列图中填上数据说明.
主视图 俯视图
图1
(2)如图2,根据左视图和俯视图,能确定小正方体个数吗?请在行列图中填上数据说明.
左视图 俯视图
图2
(3)如图3,根据主视图和左视图,能确定小正方体个数吗?请在行列图中填上数据说明.
主视图 左视图
图3
【提示】(1)有俯视图的直接用它作为行列图,由主视图可知左侧位置1个,右侧最多3个.
如图①,小正方体有1+3+1=5(个),或者1+3+2=6(个),或者1+3+3=7(个).
图①
(2)有俯视图的直接用它作为行列图,由左视图可知后排最多3个,前排位置2个.
如图②,小正方体有2+3+1=6(个),或者2+3+2=7(个),或者2+3+3=8(个).
图②
(3)由主视图可知左右两列,左侧最多1个,右侧最多3个;由左视图可知前后两行,前排最多2个,后排最多3个.
如图③,小正方体有1+3+2+0=6(个),或者1+3+2+1=7(个).
图③
归纳:小正方体组成几何体的视图与数量关系:对于在小正方体组成的几何体,结合左视图或主视图,在俯视图中标注出位于每一个位置上小正方体的层数,从而得到所有小正方体的数量;反之,由俯视图中标注的层数,能想象出几何体的形状,从而得到左视图和主视图.
意图:通过小正方体组成几何体的三视图判断小正方体的数量,然后探索在两个视图的情况下,小正方体的数量,一方面通过视图与几何体的转化培养空间想象能力,另一方面感知当物体一定时,视图是确定的,但视图确定时,物体不一定唯一.
(三)课堂练习
1.教材第100页练习第1(1)题,第2题.
2.如图,是由一些棱长为1cm的小正方体构成的立体图形的三种视图,那么这个立体图形的表面积是( B )
A.12cm2 B.14cm2 C.16cm2 D.18cm2
【提示】立体图形的形状如图所示,则其表面积为:2×(2+2+3)=14(cm2),故选B.
3.几个相同的正方体叠合在一起,该组合体的主视图和俯视图如图所示,那么组合体中正方体的个数至少有几个?至多有几个?
解:正方体最少的情况如图1所示,此时正方体有1×4+2×2=8(个);
正方体最多的情况如图2所示,此时正方体有1×2+2×4=10(个).
意图:通过教材练习题和补充习题,进一步熟悉三视图有关的计算和计数问题.针对学生的解答情况,及时反馈信息,调整教学方式和教学内容.
(四)课堂小结
教师提问:
1.由三视图求几何体的体积或表面积,一般步骤是怎样的?
2.对于由小正方体组成的几何体,怎样通过三视图或其中两个视图,判断小正方体的个数?
3.做三视图与表面展开图,都是把立体图形转化为平面图形,那么三视图、立体图与展开图三者之间有什么关系?
在学生自由发言的基础上,与同伴进行交流,师生共同总结.
意图:鼓励学生通过回顾本节课所学知识,梳理总结主要解题方法,深化对转化思想的认识.
(五)作业布置
A组:教材第102页习题29.2第5,9,10题.
B组:
1.由若干个相同的小正方体搭成的一个几何体的主视图和俯视图如图所示,则组成这个几何体的小正方体的个数是 5或6 .
2.根据三视图描述物体的形状,试画出物体的表面展开图.
解:物体的形状如图1所示,表面展开图如图2所示:
图1 图2
3.在某儿童游乐园门口需要修建一个由正方体和圆柱组合而成的立体图形,如图所示,已知正方体的棱长与圆柱的直径及高相等,都是1 m.
(1)请画出该立体图形的三视图;
(2)为了好看,需要在该立体图形表面刷一层油漆,已知油漆每平方米30元,那么一共需要花费多少元?(结果精确到0.1)
解:(1)该立体图形的三视图如图所示.
(2)根据题意得,该立体图形表面需要刷油漆的面积为
1×1×5+π×1×1=(5+π)(m2),
则 30×(5+π)≈244.2(元).
答:一共需要花费约244.2元.
意图:A组为教材题目,注重基础知识和基本技能的训练;B组题目综合性稍强,供学有余力的同学选用.
六、板书设计
七、课后反思
本章教科书在编写中先后安排了“由物画图”和“由图想物”两类问题,它们各有侧重承担了不同的任务,前者可以使人认识到立体图形的投影是什么样的平面图形,后者可以使人把相关的平面图形在头脑中综合成为相应的立体图形.两者又是互相联系的,同样的投影规则(规律)在两类问题中都是考虑问题的依据.不论“由物画图”,还是“由图想物”,都要根据投影规则(规律)进行思考,这些投影规则(规律)就是两者之间的联系,两类问题实际上是从相反的角度(方向)认识同一规律.
1
(第3课时)
一、教学内容分析
本章对于“三视图”的学习,从两方面来反映平面图形与立体图形的联系.一是画形状简单的几何体的三视图,由立体图形得到相应平面图形的过程,即“由物画图”;二是由三视图想出相应物体形状的内容,这些是由平面图形得到相应立体图形的过程,即“由图想物”,本课时是在上一课时基础上继续研究“由图想物”,涉及三视图与表面展开图两种不同的立体图形平面化处理方式,研究与三视图有关的计算问题.
二、教学目标
1.会根据三视图想象物体的表面展开图;
2.根据三视图形状和数据进行计算,会确定组成立体图形的小正方体个数.
3.在经历“三视图——实物(几何体)——展开图”的探索过程中,进一步发展几何直观和空间观念,体会转化思想;
三、教学重难点
【重点】探索三视图、实物(几何体)、展开图三者之间的转化关系.
【难点】利用三视图中的数据信息进行计算或计数.
四、教学方法
演示法.由于初中学生的三维空间观念尚未成熟,想象空间中几何元素的位置关系有一定困难,所以在教学中适当利用几何体或者实物模型(比如不同形状的纸盒)进行演示说明,让学生有初步感知,再逐步培养在脑海中想象物体形状、位置和大小关系.
五、教学过程
(一)新课导入
问题1 一个无盖盒子的三视图如图所示,请画出它的实物图,并说出这个盒子长、宽、高的尺寸单位:cm).
【提示】这个盒子的实物图如图所示,长200cm,宽100cm,高50cm.
问题2 一个物体的三视图如图所示,请画出这个物体的实物图和它的表面展开图.
【提示】这个物体的实物图和它的表面展开图如图所示.
其中,表面展开图由于剪开的线不同,得到的图形也不一定相同.
意图:通过以上复习建立三视图、实物图、展开图之间的初步关系,并明确长、宽、高所反映在不同图示中的关系.
(二)新课讲授
活动一 根据三视图计算物体的表面积
例5 某工厂要加工一批密封罐,设计者给出了密封罐的三视图(如下图),请按照三视图确定制作每个密封罐所需钢板的面积(图中尺寸单位:mm).
思考:
(1)你能由三视图想象出密封罐的形状吗?
(2)密封罐由哪几部分组成,各部分是什么形状?请说出尺寸.
(3)根据密封罐各部分可以得到密封罐的表面展开图吗?
(4)求制作每个密封罐所需钢板的面积,就是求密封罐的什么面积?怎样计算?
解:由三视图可知,密封罐的形状是正六棱柱,如图1所示.
密封罐的高为50 mm,底面正六边形的直径为100 mm,边长为50 mm,
图2是它的展开图.
图1 图2
由展开图可知,制作一个密封罐所需钢板的面积为
归纳:三视图与展开图都是把立体图形平面化处理的方式,三者之间可以相互转化.
总结:由三视图求几何体表面积的一般步骤:
①立体化:根据给出的三视图得到立体图形,并确定立体图形的长、宽、高;
②平面化:将立体图形展开得到表面展开图,观察它的组成部分;
③数量化:根据展开图的相应数据,求出展开图的面积,即得几何体的表面积.
意图:通过具体问题情境,进一步认识三视图、实物图、展开图之间的转化关系,以及在此转化过程中线、面、数据的对应关系,进行相关的计算.
活动二 根据视图求小正方体的数量
问题:由几个相同的小正方体搭成的几何体的三视图如图所示,那么几何体中一共有几个小正方体?
探索:(1)画图描述几何体的形状.
(2)在如图所示的行列图中,填上每部分的小正方体个数.
(3)这个几何体中一共有几个小正方体?
【提示】(1)如图所示:
(2)如图所示:
(3)这个几何体中的小正方体一共有1+3+2=6(个).
思考:(1)如图1,根据主视图和俯视图,能确定小正方体个数吗?请在行列图中填上数据说明.
主视图 俯视图
图1
(2)如图2,根据左视图和俯视图,能确定小正方体个数吗?请在行列图中填上数据说明.
左视图 俯视图
图2
(3)如图3,根据主视图和左视图,能确定小正方体个数吗?请在行列图中填上数据说明.
主视图 左视图
图3
【提示】(1)有俯视图的直接用它作为行列图,由主视图可知左侧位置1个,右侧最多3个.
如图①,小正方体有1+3+1=5(个),或者1+3+2=6(个),或者1+3+3=7(个).
图①
(2)有俯视图的直接用它作为行列图,由左视图可知后排最多3个,前排位置2个.
如图②,小正方体有2+3+1=6(个),或者2+3+2=7(个),或者2+3+3=8(个).
图②
(3)由主视图可知左右两列,左侧最多1个,右侧最多3个;由左视图可知前后两行,前排最多2个,后排最多3个.
如图③,小正方体有1+3+2+0=6(个),或者1+3+2+1=7(个).
图③
归纳:小正方体组成几何体的视图与数量关系:对于在小正方体组成的几何体,结合左视图或主视图,在俯视图中标注出位于每一个位置上小正方体的层数,从而得到所有小正方体的数量;反之,由俯视图中标注的层数,能想象出几何体的形状,从而得到左视图和主视图.
意图:通过小正方体组成几何体的三视图判断小正方体的数量,然后探索在两个视图的情况下,小正方体的数量,一方面通过视图与几何体的转化培养空间想象能力,另一方面感知当物体一定时,视图是确定的,但视图确定时,物体不一定唯一.
(三)课堂练习
1.教材第100页练习第1(1)题,第2题.
2.如图,是由一些棱长为1cm的小正方体构成的立体图形的三种视图,那么这个立体图形的表面积是( B )
A.12cm2 B.14cm2 C.16cm2 D.18cm2
【提示】立体图形的形状如图所示,则其表面积为:2×(2+2+3)=14(cm2),故选B.
3.几个相同的正方体叠合在一起,该组合体的主视图和俯视图如图所示,那么组合体中正方体的个数至少有几个?至多有几个?
解:正方体最少的情况如图1所示,此时正方体有1×4+2×2=8(个);
正方体最多的情况如图2所示,此时正方体有1×2+2×4=10(个).
意图:通过教材练习题和补充习题,进一步熟悉三视图有关的计算和计数问题.针对学生的解答情况,及时反馈信息,调整教学方式和教学内容.
(四)课堂小结
教师提问:
1.由三视图求几何体的体积或表面积,一般步骤是怎样的?
2.对于由小正方体组成的几何体,怎样通过三视图或其中两个视图,判断小正方体的个数?
3.做三视图与表面展开图,都是把立体图形转化为平面图形,那么三视图、立体图与展开图三者之间有什么关系?
在学生自由发言的基础上,与同伴进行交流,师生共同总结.
意图:鼓励学生通过回顾本节课所学知识,梳理总结主要解题方法,深化对转化思想的认识.
(五)作业布置
A组:教材第102页习题29.2第5,9,10题.
B组:
1.由若干个相同的小正方体搭成的一个几何体的主视图和俯视图如图所示,则组成这个几何体的小正方体的个数是 5或6 .
2.根据三视图描述物体的形状,试画出物体的表面展开图.
解:物体的形状如图1所示,表面展开图如图2所示:
图1 图2
3.在某儿童游乐园门口需要修建一个由正方体和圆柱组合而成的立体图形,如图所示,已知正方体的棱长与圆柱的直径及高相等,都是1 m.
(1)请画出该立体图形的三视图;
(2)为了好看,需要在该立体图形表面刷一层油漆,已知油漆每平方米30元,那么一共需要花费多少元?(结果精确到0.1)
解:(1)该立体图形的三视图如图所示.
(2)根据题意得,该立体图形表面需要刷油漆的面积为
1×1×5+π×1×1=(5+π)(m2),
则 30×(5+π)≈244.2(元).
答:一共需要花费约244.2元.
意图:A组为教材题目,注重基础知识和基本技能的训练;B组题目综合性稍强,供学有余力的同学选用.
六、板书设计
七、课后反思
本章教科书在编写中先后安排了“由物画图”和“由图想物”两类问题,它们各有侧重承担了不同的任务,前者可以使人认识到立体图形的投影是什么样的平面图形,后者可以使人把相关的平面图形在头脑中综合成为相应的立体图形.两者又是互相联系的,同样的投影规则(规律)在两类问题中都是考虑问题的依据.不论“由物画图”,还是“由图想物”,都要根据投影规则(规律)进行思考,这些投影规则(规律)就是两者之间的联系,两类问题实际上是从相反的角度(方向)认识同一规律.
1
