初中数学人教版九下29.2三视图(第1课时) 教案
文档属性
| 名称 | 初中数学人教版九下29.2三视图(第1课时) 教案 |

|
|
| 格式 | doc | ||
| 文件大小 | 1.3MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-09-12 00:00:00 | ||
图片预览


文档简介
29.2三视图
(第1课时)
一、教学内容分析
三视图知识建立在正投影的基础之上,由于涉及空间的位置关系,对学生而言,具备一定的空间想象能力是学习这部分知识的前提.本节讨论的重点是三视图,包括三视图的成像原理、三视图的位置和度量规定、一些基本几何体的三视图等.这一节也是全章的重点内容,它不仅包括了有关三视图的基本概念和规律,而且包括了反映立体图形和平面图形的联系与转化的内容,与培养空间想象能力有直接的关系.其中,本课时主要有三视图的概念、规则以及画形状简单的几何体的三视图,这些是由立体图形得到相应平面图形的过程.
二、教学目标
1.理解三视图的基本概念,探索三个视图之间的位置关系和大小关系.
2.通过讨论简单立体图形三视图,使学生经历画图和识图,分析立体图形转化为平面图形的过程,提高空间想象能力.
三、教学重难点
【重点】从正投影的角度理解三视图的概念和基本特征.
【难点】能画出简单几何体的三视图.
四、教学方法
课堂讨论法.在学习本节课知识之前,学生已经具备了相关的知识经验,比如七年级学习的“从不同方向观察物体”和上节课学习的正投影等,加之本节课无需太多的计算和推理,所以对于很多学生的知识储备而言,几乎在同一起点水平上,这为课堂讨论提供了有力保障.
五、教学过程
(一)新课导入
观察:如图为某飞机的外形设计图,你能指出这些设计图是从哪几个方向观察得到的吗?
【提示】分别是从正面、左面和上面看得到的.
思考:它们分别可以看作飞机在哪个方向光线下的正投影?
意图:回顾“从不同方向观察物体”,与不同方向投影线下的正投影对照,把两个知识有机衔接,为后续得到“视图”概念做好铺垫.
(二)新课讲授
活动一 学习视图的概念
观察:请同学们观察桌面上直立摆放的书,你能说出下面图形分别是从什么方向观察时得到的吗?
定义:当我们从某一方向观察一个物体时,所看到的平面图形叫做物体的一个视图.
归纳:视图可以看作物体在某一方向光线下的正投影.
思考:
1.以上三个视图可以看作词典在哪个方向光线下的正投影?
2.由三个视图分别能得到这本词典的什么数学信息?
演示:我们用三个互相垂直的平面(例如墙角处的三面墙)作为投影面,其中正对着我们的面叫做正面,正面下方的面叫做水平面,右边的叫做侧面.对一个长方体在三个投影面内同时进行正投影,得到三个视图,如图所示.
定义:在正面内得到的由前向后观察物体的视图,叫做主视图;
在水平面内得到的由上向下观察物体的视图,叫做俯视图;
在侧面内得到的由左向右观察物体的视图,叫做左视图.
归纳:
1.三视图与以前我们学习的从三个方向看物体的得到的平面图形是一致的、现在我们从投影的角度认识这个问题,并且对三个方向做出明确的规定.
2.物体的三视图实际上是物体在三个不同方向的正投影.
将三个投影面展开在一个平面内,得到这一物体的三视图.
正面上的正投影就是主视图,水平面上的正投影就是俯视图,侧面上的正投影就是左视图.
3.三视图是主视图、俯视图、左视图的统称.
它是从三个方向分别表示物体形状的一种常用视图.
三视图中的各视图,分别从不同方面表示物体的形状,三者结合起来能够较全面地反映物体的形状.
意图:结合具体的情境,形成视图、主视图、俯视图、左视图、三视图等基本概念,并进一步沟通视图与“从不同方向看”之间的关系.
活动二 探索三视图的性质
演示:通过动画演示,介绍物体的长、宽、高.
正对着物体看:
物体左右之间的水平距离是物体的长;
前后之间的水平距离是物体的宽;
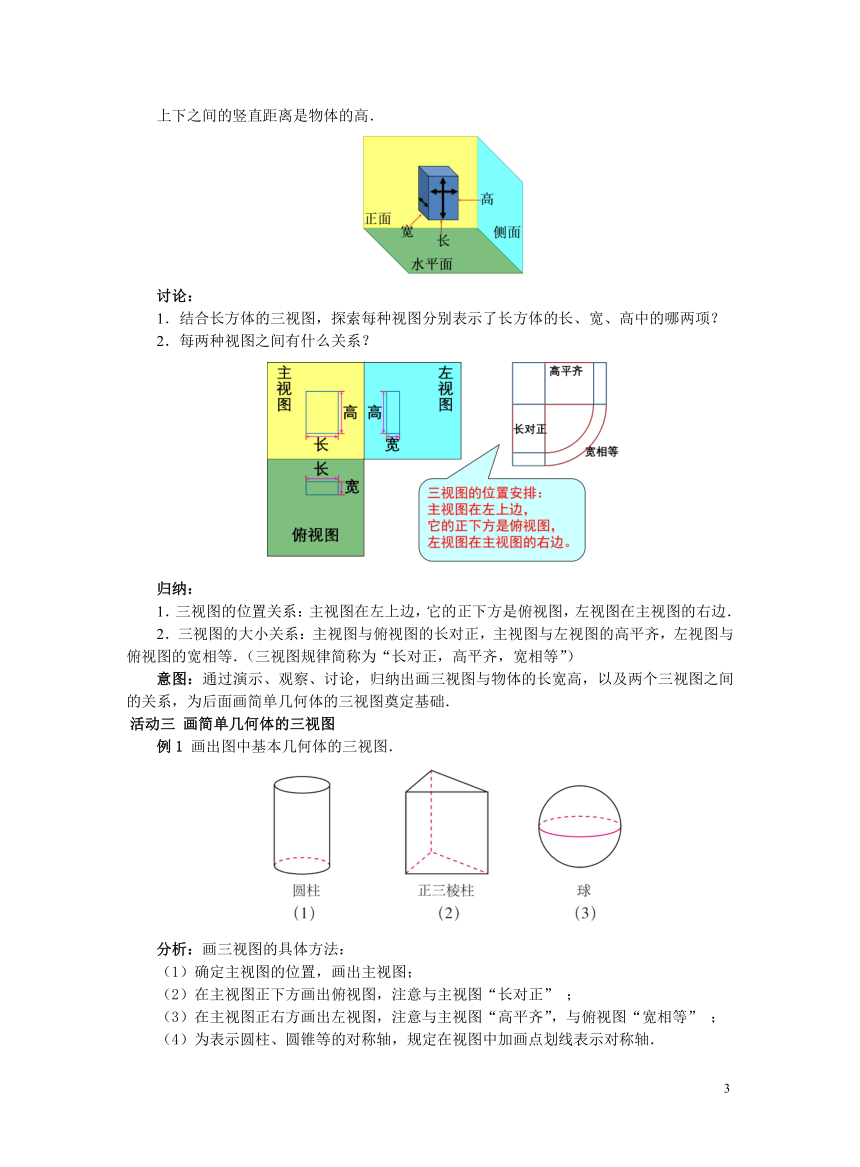
上下之间的竖直距离是物体的高.
讨论:
1.结合长方体的三视图,探索每种视图分别表示了长方体的长、宽、高中的哪两项?
2.每两种视图之间有什么关系?
归纳:
1.三视图的位置关系:主视图在左上边,它的正下方是俯视图,左视图在主视图的右边.
2.三视图的大小关系:主视图与俯视图的长对正,主视图与左视图的高平齐,左视图与俯视图的宽相等.(三视图规律简称为“长对正,高平齐,宽相等”)
意图:通过演示、观察、讨论,归纳出画三视图与物体的长宽高,以及两个三视图之间的关系,为后面画简单几何体的三视图奠定基础.
活动三 画简单几何体的三视图
例1 画出图中基本几何体的三视图.
分析:画三视图的具体方法:
(1)确定主视图的位置,画出主视图;
(2)在主视图正下方画出俯视图,注意与主视图“长对正” ;
(3)在主视图正右方画出左视图,注意与主视图“高平齐”,与俯视图“宽相等” ;
(4)为表示圆柱、圆锥等的对称轴,规定在视图中加画点划线表示对称轴.
解:如图所示:
注意:对于正三棱柱的三视图注意以下两点:
1.看得见部分的轮廓线画成实线,因被其他部分遮挡而看不见的轮廓线画成虚线.
2.“宽相等”,这里的“宽”是指正三棱柱中底面等边三角形的高,而非边长.
例2 画出如图所示的支架(一种小零件)的三视图,其中支架的两个台阶的高度和宽度相等.
思考:
1.图示的支架可以分解为哪两个几何体?
2.画三视图时,如何遵循三视图的位置关系和大小关系?
意图:结合具体实例,进一步理解画三视图的一般方法,特别是三视图的位置关系和大小关系.
(三)课堂练习
1.教材第97页练习题.
2.如图是两个等直径圆柱构成的“T”形管道,其左视图是( B )
B. C. D.
3.图中的立体图形可以看成有哪些基本几何体经过怎样的变化得到的?画出它的三视图.
解:这个立体图形可以看成圆柱体中间挖去一个长方体而成,
三视图如图所示.
【提示】看得见部分的轮廓线画成实线,因被其他部分遮挡而看不见的轮廓线画成虚线.
意图:通过三视图的判断、识别与画图巩固本节课所学知识,并以第3题为例说明“看不见的轮廓线画成虚线”,补充三视图的画图规则.
(四)课堂小结
教师提问:
1.视图与“从不同方向看物体”有什么联系?
2.请从投影的角度说说三视图中三个视图的产生过程.
3.在三视图中,各视图之间有怎样的位置关系和大小关系?
4.画基本几何体的三视图的方法(或注意点).
在学生自由发言的基础上,与同伴进行交流,师生共同总结.
意图:结合课堂中的实例或者举出新的例子,对小节中的内容加以说明,及时梳理知识,纳入已有知识网络体系.
(五)作业布置
A组:教材第101页习题29.2第1,2,3,6,7题.
B组:
1.如图,下列关于物体的主视图画法正确的是( C )
2. 下图的几何体中,主视图、左视图、俯视图均相同的是( D )
3.画出如图所示立体图形的三视图.
解:三视图如图所示.
意图:A组题目注重基础知识,画三视图的物体主要涉及简单的单一几何体或两个规范几何体的组合,B组题目的问题情境稍微复杂些,带有一定综合性,供学有余力的同学选用.
六、板书设计
七、课后反思
在学习本章之前,学生已经具有一定的关于平面图形与立体图形的知识,并且接触过“从不同方向观察物体”、正投影等相关知识,学习本课时内容,应多联系学生已有的知识基础和生活经验.本课时从投影的角度对如何用三视图这样的平面图形来表示三维立体图形进行进一步讨论,这有助于将学生对于图形已有的认识加以提高,进一步培养空间想象能力.
1
(第1课时)
一、教学内容分析
三视图知识建立在正投影的基础之上,由于涉及空间的位置关系,对学生而言,具备一定的空间想象能力是学习这部分知识的前提.本节讨论的重点是三视图,包括三视图的成像原理、三视图的位置和度量规定、一些基本几何体的三视图等.这一节也是全章的重点内容,它不仅包括了有关三视图的基本概念和规律,而且包括了反映立体图形和平面图形的联系与转化的内容,与培养空间想象能力有直接的关系.其中,本课时主要有三视图的概念、规则以及画形状简单的几何体的三视图,这些是由立体图形得到相应平面图形的过程.
二、教学目标
1.理解三视图的基本概念,探索三个视图之间的位置关系和大小关系.
2.通过讨论简单立体图形三视图,使学生经历画图和识图,分析立体图形转化为平面图形的过程,提高空间想象能力.
三、教学重难点
【重点】从正投影的角度理解三视图的概念和基本特征.
【难点】能画出简单几何体的三视图.
四、教学方法
课堂讨论法.在学习本节课知识之前,学生已经具备了相关的知识经验,比如七年级学习的“从不同方向观察物体”和上节课学习的正投影等,加之本节课无需太多的计算和推理,所以对于很多学生的知识储备而言,几乎在同一起点水平上,这为课堂讨论提供了有力保障.
五、教学过程
(一)新课导入
观察:如图为某飞机的外形设计图,你能指出这些设计图是从哪几个方向观察得到的吗?
【提示】分别是从正面、左面和上面看得到的.
思考:它们分别可以看作飞机在哪个方向光线下的正投影?
意图:回顾“从不同方向观察物体”,与不同方向投影线下的正投影对照,把两个知识有机衔接,为后续得到“视图”概念做好铺垫.
(二)新课讲授
活动一 学习视图的概念
观察:请同学们观察桌面上直立摆放的书,你能说出下面图形分别是从什么方向观察时得到的吗?
定义:当我们从某一方向观察一个物体时,所看到的平面图形叫做物体的一个视图.
归纳:视图可以看作物体在某一方向光线下的正投影.
思考:
1.以上三个视图可以看作词典在哪个方向光线下的正投影?
2.由三个视图分别能得到这本词典的什么数学信息?
演示:我们用三个互相垂直的平面(例如墙角处的三面墙)作为投影面,其中正对着我们的面叫做正面,正面下方的面叫做水平面,右边的叫做侧面.对一个长方体在三个投影面内同时进行正投影,得到三个视图,如图所示.
定义:在正面内得到的由前向后观察物体的视图,叫做主视图;
在水平面内得到的由上向下观察物体的视图,叫做俯视图;
在侧面内得到的由左向右观察物体的视图,叫做左视图.
归纳:
1.三视图与以前我们学习的从三个方向看物体的得到的平面图形是一致的、现在我们从投影的角度认识这个问题,并且对三个方向做出明确的规定.
2.物体的三视图实际上是物体在三个不同方向的正投影.
将三个投影面展开在一个平面内,得到这一物体的三视图.
正面上的正投影就是主视图,水平面上的正投影就是俯视图,侧面上的正投影就是左视图.
3.三视图是主视图、俯视图、左视图的统称.
它是从三个方向分别表示物体形状的一种常用视图.
三视图中的各视图,分别从不同方面表示物体的形状,三者结合起来能够较全面地反映物体的形状.
意图:结合具体的情境,形成视图、主视图、俯视图、左视图、三视图等基本概念,并进一步沟通视图与“从不同方向看”之间的关系.
活动二 探索三视图的性质
演示:通过动画演示,介绍物体的长、宽、高.
正对着物体看:
物体左右之间的水平距离是物体的长;
前后之间的水平距离是物体的宽;
上下之间的竖直距离是物体的高.
讨论:
1.结合长方体的三视图,探索每种视图分别表示了长方体的长、宽、高中的哪两项?
2.每两种视图之间有什么关系?
归纳:
1.三视图的位置关系:主视图在左上边,它的正下方是俯视图,左视图在主视图的右边.
2.三视图的大小关系:主视图与俯视图的长对正,主视图与左视图的高平齐,左视图与俯视图的宽相等.(三视图规律简称为“长对正,高平齐,宽相等”)
意图:通过演示、观察、讨论,归纳出画三视图与物体的长宽高,以及两个三视图之间的关系,为后面画简单几何体的三视图奠定基础.
活动三 画简单几何体的三视图
例1 画出图中基本几何体的三视图.
分析:画三视图的具体方法:
(1)确定主视图的位置,画出主视图;
(2)在主视图正下方画出俯视图,注意与主视图“长对正” ;
(3)在主视图正右方画出左视图,注意与主视图“高平齐”,与俯视图“宽相等” ;
(4)为表示圆柱、圆锥等的对称轴,规定在视图中加画点划线表示对称轴.
解:如图所示:
注意:对于正三棱柱的三视图注意以下两点:
1.看得见部分的轮廓线画成实线,因被其他部分遮挡而看不见的轮廓线画成虚线.
2.“宽相等”,这里的“宽”是指正三棱柱中底面等边三角形的高,而非边长.
例2 画出如图所示的支架(一种小零件)的三视图,其中支架的两个台阶的高度和宽度相等.
思考:
1.图示的支架可以分解为哪两个几何体?
2.画三视图时,如何遵循三视图的位置关系和大小关系?
意图:结合具体实例,进一步理解画三视图的一般方法,特别是三视图的位置关系和大小关系.
(三)课堂练习
1.教材第97页练习题.
2.如图是两个等直径圆柱构成的“T”形管道,其左视图是( B )
B. C. D.
3.图中的立体图形可以看成有哪些基本几何体经过怎样的变化得到的?画出它的三视图.
解:这个立体图形可以看成圆柱体中间挖去一个长方体而成,
三视图如图所示.
【提示】看得见部分的轮廓线画成实线,因被其他部分遮挡而看不见的轮廓线画成虚线.
意图:通过三视图的判断、识别与画图巩固本节课所学知识,并以第3题为例说明“看不见的轮廓线画成虚线”,补充三视图的画图规则.
(四)课堂小结
教师提问:
1.视图与“从不同方向看物体”有什么联系?
2.请从投影的角度说说三视图中三个视图的产生过程.
3.在三视图中,各视图之间有怎样的位置关系和大小关系?
4.画基本几何体的三视图的方法(或注意点).
在学生自由发言的基础上,与同伴进行交流,师生共同总结.
意图:结合课堂中的实例或者举出新的例子,对小节中的内容加以说明,及时梳理知识,纳入已有知识网络体系.
(五)作业布置
A组:教材第101页习题29.2第1,2,3,6,7题.
B组:
1.如图,下列关于物体的主视图画法正确的是( C )
2. 下图的几何体中,主视图、左视图、俯视图均相同的是( D )
3.画出如图所示立体图形的三视图.
解:三视图如图所示.
意图:A组题目注重基础知识,画三视图的物体主要涉及简单的单一几何体或两个规范几何体的组合,B组题目的问题情境稍微复杂些,带有一定综合性,供学有余力的同学选用.
六、板书设计
七、课后反思
在学习本章之前,学生已经具有一定的关于平面图形与立体图形的知识,并且接触过“从不同方向观察物体”、正投影等相关知识,学习本课时内容,应多联系学生已有的知识基础和生活经验.本课时从投影的角度对如何用三视图这样的平面图形来表示三维立体图形进行进一步讨论,这有助于将学生对于图形已有的认识加以提高,进一步培养空间想象能力.
1
