初中数学人教版九下29.2三视图(第2课时) 教案
文档属性
| 名称 | 初中数学人教版九下29.2三视图(第2课时) 教案 |  | |
| 格式 | doc | ||
| 文件大小 | 1.0MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-09-12 22:44:00 | ||
图片预览

文档简介
29.2三视图
(第2课时)
一、教学内容分析
三视图是本章的重点内容,从两方面来研究平面图形与立体图形的联系,上一课时主要有三视图的概念、规则以及画形状简单的几何体的三视图,这些是由立体图形得到相应平面图形的过程;本课时主要为由三视图想出相应物体形状的内容,这些是由平面图形得到相应立体图形的过程.两方面结合起来,就从不同角度反映了平面图形与相应的立体图形是如何联系的.从技能上说,认识平面图形与立体图形的联系,有助于根据需要实现它们之间的相互转化,即学会画三视图和由三视图得出立体图形.从能力上说,认识平面图形与立体图形的联系,对于培养空间想象能力是非常重要的.
二、教学目标
1.能根据三视图想象出简单几何体的形状或实物原型,并能画出草图.
2.通过观察、操作、画图,探究三视图向立体图形的转化过程,体会二者之间的密切联系,发展几何直观和空间观念,促进空间想象能力.
三、教学重难点
【重点】根据三视图画出简单几何体的形状或实物原型.
【难点】理解三视图与几何体之间的联系与相互转化.
四、教学方法
演示法.由三视图转化为立体图形需要一定的空间想象能力,鉴于初中生的空间观念比较薄弱,所以可以通过观察几何体或实物的演示过程,借助几何直观来达成教学任务,同时培养空间观念.
五、教学过程
(一)新课导入
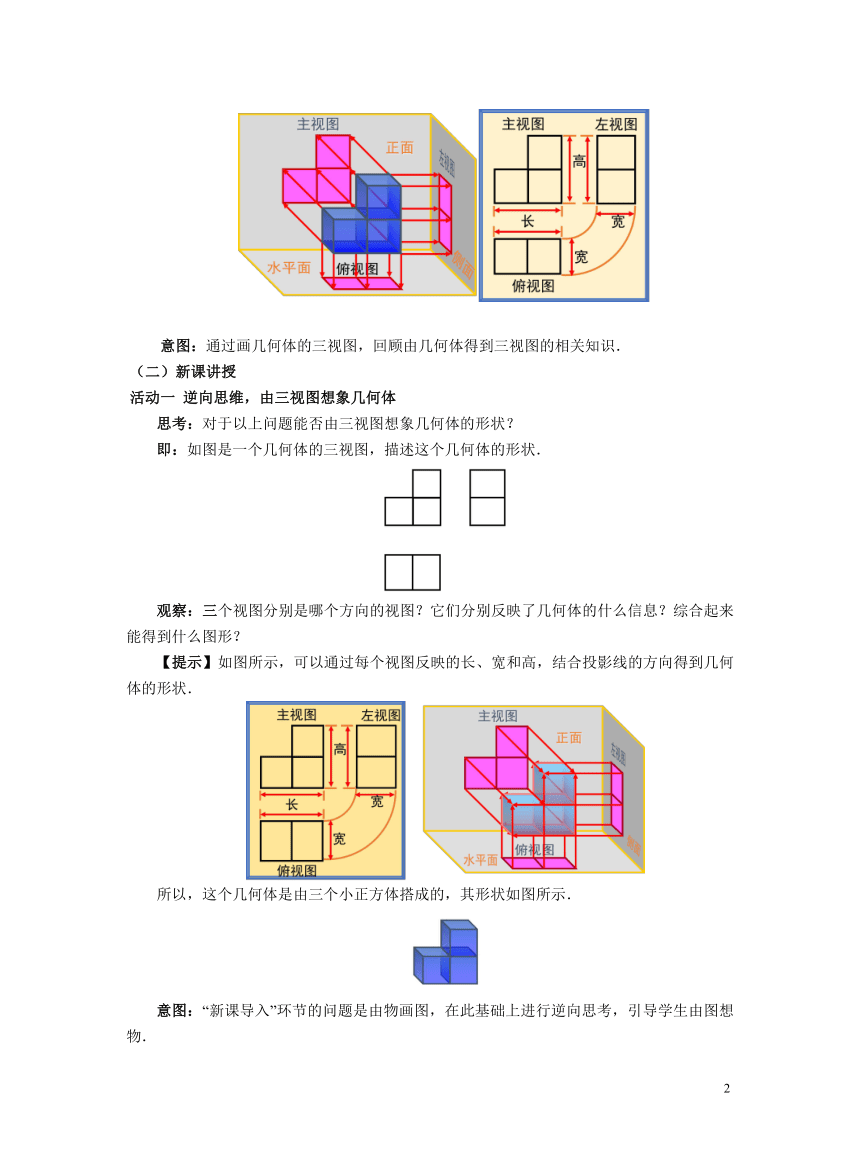
如图是由三个小正方体搭成的几何体,画出它的三视图.结合画图过程说明三视图的形成,及其相互之间的位置关系和大小关系.
【提示】如图所示:
意图:通过画几何体的三视图,回顾由几何体得到三视图的相关知识.
(二)新课讲授
活动一 逆向思维,由三视图想象几何体
思考:对于以上问题能否由三视图想象几何体的形状?
即:如图是一个几何体的三视图,描述这个几何体的形状.
观察:三个视图分别是哪个方向的视图?它们分别反映了几何体的什么信息?综合起来能得到什么图形?
【提示】如图所示,可以通过每个视图反映的长、宽和高,结合投影线的方向得到几何体的形状.
所以,这个几何体是由三个小正方体搭成的,其形状如图所示.
意图:“新课导入”环节的问题是由物画图,在此基础上进行逆向思考,引导学生由图想物.
活动二 例题讲解,培养空间想象能力
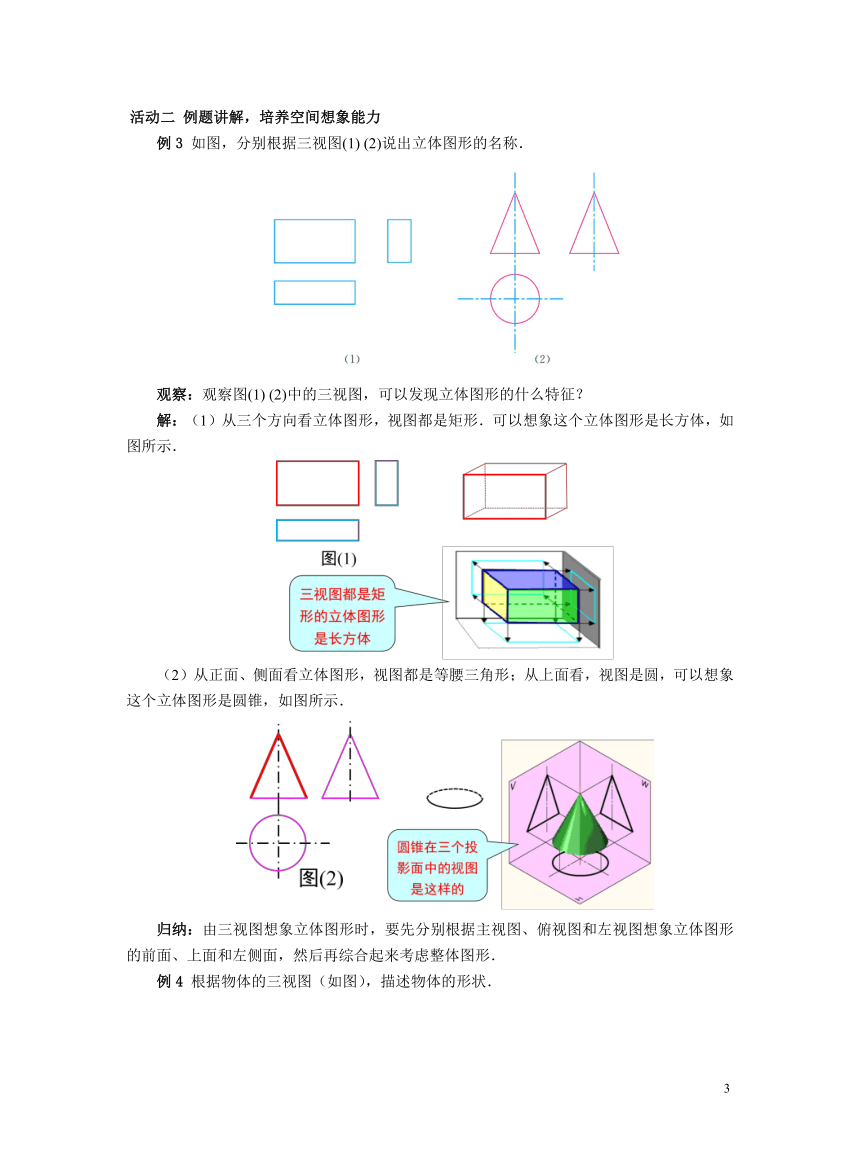
例3 如图,分别根据三视图(1) (2)说出立体图形的名称.
观察:观察图(1) (2)中的三视图,可以发现立体图形的什么特征?
解:(1)从三个方向看立体图形,视图都是矩形.可以想象这个立体图形是长方体,如图所示.
(2)从正面、侧面看立体图形,视图都是等腰三角形;从上面看,视图是圆,可以想象这个立体图形是圆锥,如图所示.
归纳:由三视图想象立体图形时,要先分别根据主视图、俯视图和左视图想象立体图形的前面、上面和左侧面,然后再综合起来考虑整体图形.
例4 根据物体的三视图(如图),描述物体的形状.
思考:三视图中各线条分别是想象的立体图形哪部分的投影?
解:物体是正五棱柱形状的,如图所示.
归纳:将三视图还原成实物图,可以从以下几方面考虑:
(1)通过视图,分析几何体是简单几何体还是组合体;
(2)联系三个视图,分析该几何体的各基本部分的形状;
(3)弄清楚视图上各条线的意义——是轮廓线还是轮廓线的投影;
(4)注意图中的虚线和实线;
(5)将画出的实物图和三视图对照检查.
意图:通过对典型问题的分析,进一步提高由三视图想象几何体或物体原型的能力,总结出基本方法和注意事项.
(三)课堂练习
1.教材第99页练习题.
2.如图,根据几何体的三视图,画出几何体.
解:几何体如图所示.
3.如图,根据物体的三视图,描述物体的形状.
解:物体是四棱柱形状的,如图所示.
意图:运用所学方法由三视图想象几何图形,培养基本技能的形成,发展空间观念.
(四)课堂小结
教师提问:
1.一个几何体或者物体的三视图中分别是从哪个角度观察得到的?它们分别反映了几何体或者物体的哪些面或线的特征?
2.总结几种常见三视图的几何体原型.
在学生自由发言的基础上,与同伴进行交流,师生共同总结.
意图:鼓励学生根据自己的知识经验大胆发言,不追统一答案.
(五)作业布置
A组:教材第102页习题29.2第4,5题.
B组:教材第103页习题29.2第9题.
意图:A组题目注重简单问题的解决,B组题目有一定综合性,供学有余力的同学选用.
六、板书设计
七、课后反思
空间想象能力是一种重要的数学基本能力,本章内容非常适合培养这种能力.本章所讨论的对象是投影与视图,其中没有很多计算问题,也没有形式上的推理证明,这与前面几章形成明显的区别.本章面临的主要是立体图形与平面图形的相互转化问题,而掌握立体图形与相应平面图形的联系是实现上述转化的关键.要掌握这种联系,不仅需要认识从立体图形到平面图形的转化过程,还需要认识从平面图形到立体图形的转化过程,即需要从两方面双向地认识这种联系.
1
(第2课时)
一、教学内容分析
三视图是本章的重点内容,从两方面来研究平面图形与立体图形的联系,上一课时主要有三视图的概念、规则以及画形状简单的几何体的三视图,这些是由立体图形得到相应平面图形的过程;本课时主要为由三视图想出相应物体形状的内容,这些是由平面图形得到相应立体图形的过程.两方面结合起来,就从不同角度反映了平面图形与相应的立体图形是如何联系的.从技能上说,认识平面图形与立体图形的联系,有助于根据需要实现它们之间的相互转化,即学会画三视图和由三视图得出立体图形.从能力上说,认识平面图形与立体图形的联系,对于培养空间想象能力是非常重要的.
二、教学目标
1.能根据三视图想象出简单几何体的形状或实物原型,并能画出草图.
2.通过观察、操作、画图,探究三视图向立体图形的转化过程,体会二者之间的密切联系,发展几何直观和空间观念,促进空间想象能力.
三、教学重难点
【重点】根据三视图画出简单几何体的形状或实物原型.
【难点】理解三视图与几何体之间的联系与相互转化.
四、教学方法
演示法.由三视图转化为立体图形需要一定的空间想象能力,鉴于初中生的空间观念比较薄弱,所以可以通过观察几何体或实物的演示过程,借助几何直观来达成教学任务,同时培养空间观念.
五、教学过程
(一)新课导入
如图是由三个小正方体搭成的几何体,画出它的三视图.结合画图过程说明三视图的形成,及其相互之间的位置关系和大小关系.
【提示】如图所示:
意图:通过画几何体的三视图,回顾由几何体得到三视图的相关知识.
(二)新课讲授
活动一 逆向思维,由三视图想象几何体
思考:对于以上问题能否由三视图想象几何体的形状?
即:如图是一个几何体的三视图,描述这个几何体的形状.
观察:三个视图分别是哪个方向的视图?它们分别反映了几何体的什么信息?综合起来能得到什么图形?
【提示】如图所示,可以通过每个视图反映的长、宽和高,结合投影线的方向得到几何体的形状.
所以,这个几何体是由三个小正方体搭成的,其形状如图所示.
意图:“新课导入”环节的问题是由物画图,在此基础上进行逆向思考,引导学生由图想物.
活动二 例题讲解,培养空间想象能力
例3 如图,分别根据三视图(1) (2)说出立体图形的名称.
观察:观察图(1) (2)中的三视图,可以发现立体图形的什么特征?
解:(1)从三个方向看立体图形,视图都是矩形.可以想象这个立体图形是长方体,如图所示.
(2)从正面、侧面看立体图形,视图都是等腰三角形;从上面看,视图是圆,可以想象这个立体图形是圆锥,如图所示.
归纳:由三视图想象立体图形时,要先分别根据主视图、俯视图和左视图想象立体图形的前面、上面和左侧面,然后再综合起来考虑整体图形.
例4 根据物体的三视图(如图),描述物体的形状.
思考:三视图中各线条分别是想象的立体图形哪部分的投影?
解:物体是正五棱柱形状的,如图所示.
归纳:将三视图还原成实物图,可以从以下几方面考虑:
(1)通过视图,分析几何体是简单几何体还是组合体;
(2)联系三个视图,分析该几何体的各基本部分的形状;
(3)弄清楚视图上各条线的意义——是轮廓线还是轮廓线的投影;
(4)注意图中的虚线和实线;
(5)将画出的实物图和三视图对照检查.
意图:通过对典型问题的分析,进一步提高由三视图想象几何体或物体原型的能力,总结出基本方法和注意事项.
(三)课堂练习
1.教材第99页练习题.
2.如图,根据几何体的三视图,画出几何体.
解:几何体如图所示.
3.如图,根据物体的三视图,描述物体的形状.
解:物体是四棱柱形状的,如图所示.
意图:运用所学方法由三视图想象几何图形,培养基本技能的形成,发展空间观念.
(四)课堂小结
教师提问:
1.一个几何体或者物体的三视图中分别是从哪个角度观察得到的?它们分别反映了几何体或者物体的哪些面或线的特征?
2.总结几种常见三视图的几何体原型.
在学生自由发言的基础上,与同伴进行交流,师生共同总结.
意图:鼓励学生根据自己的知识经验大胆发言,不追统一答案.
(五)作业布置
A组:教材第102页习题29.2第4,5题.
B组:教材第103页习题29.2第9题.
意图:A组题目注重简单问题的解决,B组题目有一定综合性,供学有余力的同学选用.
六、板书设计
七、课后反思
空间想象能力是一种重要的数学基本能力,本章内容非常适合培养这种能力.本章所讨论的对象是投影与视图,其中没有很多计算问题,也没有形式上的推理证明,这与前面几章形成明显的区别.本章面临的主要是立体图形与平面图形的相互转化问题,而掌握立体图形与相应平面图形的联系是实现上述转化的关键.要掌握这种联系,不仅需要认识从立体图形到平面图形的转化过程,还需要认识从平面图形到立体图形的转化过程,即需要从两方面双向地认识这种联系.
1
