初中数学人教版九下29.3课题学习 制作立体模型 教案
文档属性
| 名称 | 初中数学人教版九下29.3课题学习 制作立体模型 教案 |

|
|
| 格式 | doc | ||
| 文件大小 | 586.5KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-09-12 22:47:36 | ||
图片预览

文档简介
29.3课题学习 制作立体模型
一、教学内容分析
本节课安排的课题学习是观察、想象、制作相结合的实践活动,这是结合实际动脑与动手并重的学习内容.进行这个课题学习既可以采用独立完成的形式,也可以采用合作式学习的方式.应该把这个课题学习看作对前面学习的内容是否切实理解掌握以及能否灵活运用的一次联系实际的检验.
二、教学目标
1.根据三视图或展开图制作立体模型,进一步加深对投影和视图知识的认识.
2.在实际动手中进一步探索三视图、实物模型与展开图之间的关系,加强在实践活动中手脑结合的能力.
三、教学重难点
【重点】根据三视图或展开图制作出符合平面图形特征的立体模型.
【难点】在手工操作过程中,通过裁剪、折叠、拼接、削切等方法得到想象中的实物模型.
四、教学方法
操作演示法和合作探究法.鉴于本课时具有鲜明的综合与实践特点,并且对部分学生而言,把想象的物体通过动手操作制作成实物模型有一定挑战性,所以提倡学生在独立思考、尝试完成的前提下,开展合作学习,通过交流分享、质疑纠错、修订完善,完成学习任务.
五、教学过程
(一)课题准备
学习目的:通过由三视图制作立体模型的实践活动,体验平面图形向立体图形转化的过程,体会用三视图表示立体图形的作用,进一步感受立体图形与平面图形之间的联系.
操作工具:刻度尺、剪刀、小刀、胶水、硬纸板、马铃薯(或萝卜)等.
几点要求:
1.课题学习过程中,积极思考,由平面图形(三视图或展开图)想象立体图形的形状.
2.根据课题要求,通过裁剪、折叠、拼接、削切等方法制作实物模型.
3.解决与实物模型有关的数学问题.
4.操作过程中,工具的使用要符合规范,避免安全隐患.
5.学习过程中,首先尝试独立思考解决问题,然后进行合作交流,完善方案,分享成果.
意图:从目的、工具、要求三个方面为整节课的学习奠定总基调,特别强调独立操作与合作探究相结合,大胆操作与注意安全相结合.
(二)课题活动
活动一 用硬纸板制作立体模型
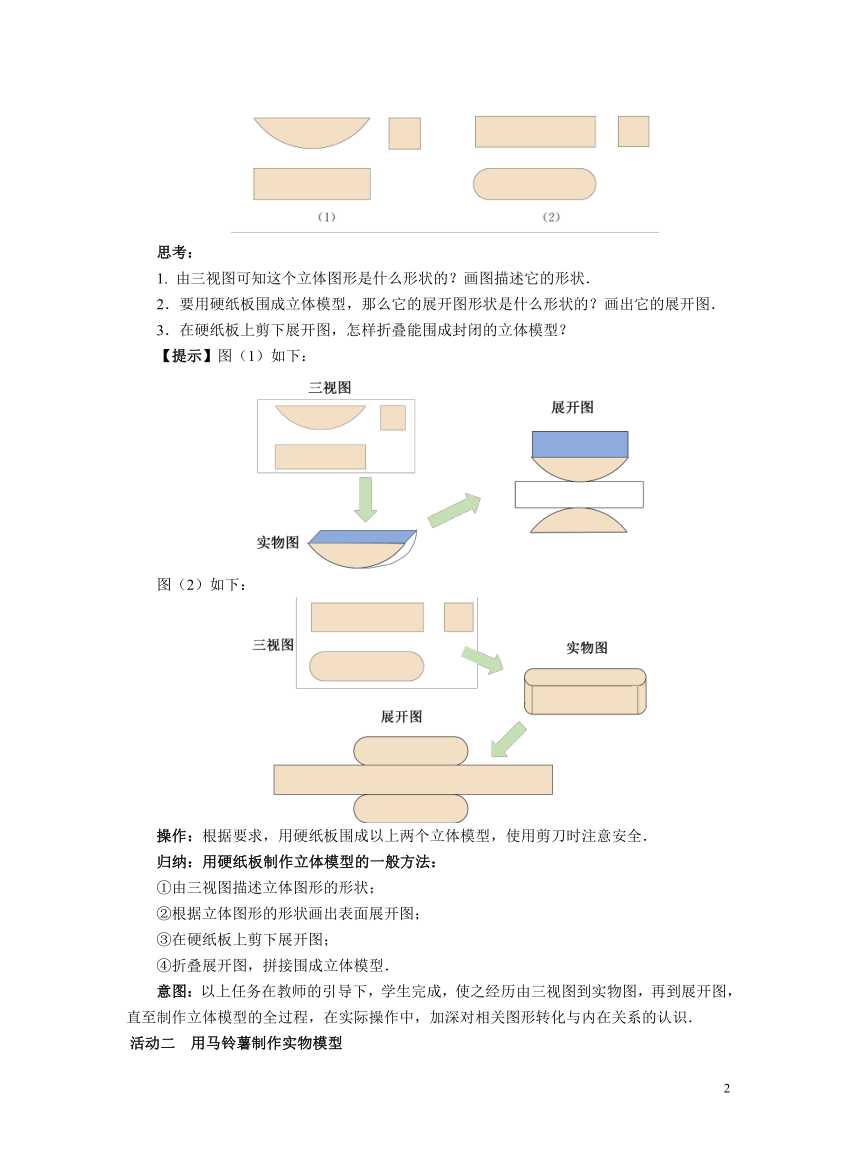
任务:以硬纸板为主要材料,分别做出下面的两组三视图(如图)表示的立体模型.
思考:
1. 由三视图可知这个立体图形是什么形状的?画图描述它的形状.
2.要用硬纸板围成立体模型,那么它的展开图形状是什么形状的?画出它的展开图.
3.在硬纸板上剪下展开图,怎样折叠能围成封闭的立体模型?
【提示】图(1)如下:
图(2)如下:
操作:根据要求,用硬纸板围成以上两个立体模型,使用剪刀时注意安全.
归纳:用硬纸板制作立体模型的一般方法:
①由三视图描述立体图形的形状;
②根据立体图形的形状画出表面展开图;
③在硬纸板上剪下展开图;
④折叠展开图,拼接围成立体模型.
意图:以上任务在教师的引导下,学生完成,使之经历由三视图到实物图,再到展开图,直至制作立体模型的全过程,在实际操作中,加深对相关图形转化与内在关系的认识.
活动二 用马铃薯制作实物模型
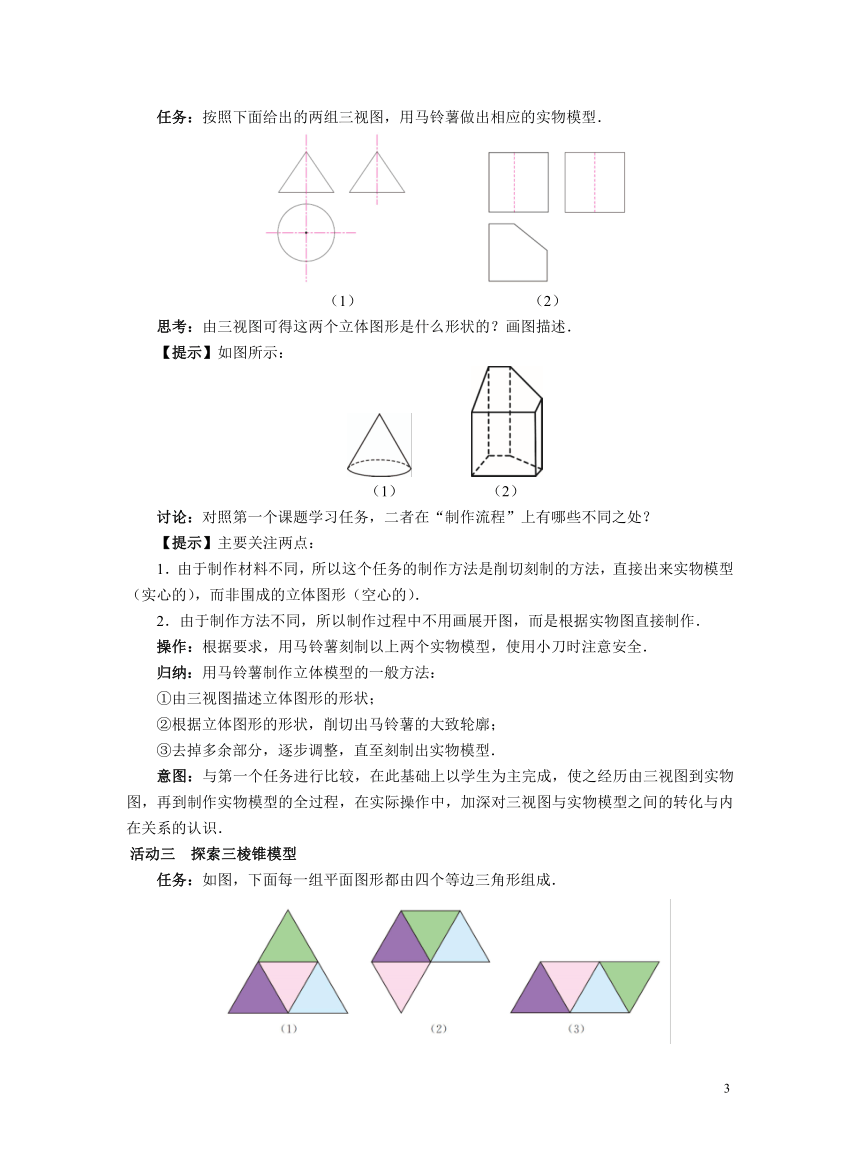
任务:按照下面给出的两组三视图,用马铃薯做出相应的实物模型.
(1) (2)
思考:由三视图可得这两个立体图形是什么形状的?画图描述.
【提示】如图所示:
(1) (2)
讨论:对照第一个课题学习任务,二者在“制作流程”上有哪些不同之处?
【提示】主要关注两点:
1.由于制作材料不同,所以这个任务的制作方法是削切刻制的方法,直接出来实物模型(实心的),而非围成的立体图形(空心的).
2.由于制作方法不同,所以制作过程中不用画展开图,而是根据实物图直接制作.
操作:根据要求,用马铃薯刻制以上两个实物模型,使用小刀时注意安全.
归纳:用马铃薯制作立体模型的一般方法:
①由三视图描述立体图形的形状;
②根据立体图形的形状,削切出马铃薯的大致轮廓;
③去掉多余部分,逐步调整,直至刻制出实物模型.
意图:与第一个任务进行比较,在此基础上以学生为主完成,使之经历由三视图到实物图,再到制作实物模型的全过程,在实际操作中,加深对三视图与实物模型之间的转化与内在关系的认识.
活动三 探索三棱锥模型
任务:如图,下面每一组平面图形都由四个等边三角形组成.
(1)其中哪些可以折叠成三棱锥?把图形描在纸上,剪下来,叠一叠,验证你的结论.
(2)画出由上面图形能折叠成的三棱锥的三视图,并指出三视图中是怎样体现“长对正,高平齐,宽相等”的.
(3)如果上图中小三角形的边长为1,那么对应的三棱锥的表面积是多少?
【提示】(1)图(1)(3)可以折叠成三棱锥.
(2)如图所示:
(3)∵,
∴.
意图:给学生更大的自主探索讨论空间,通过观察、思考、操作、对比、计算,感受三视图与立体图形在转化过程中的位置关系与数量关系.
活动四 探索圆锥模型
任务:如图所示的图形由一个扇形和一个圆组成.
(1)把图形描在纸上,剪下来,围成一个圆锥.
(2)画出由图形围成的圆锥的三视图.
(3)如果图中扇形的半径为13,圆的半径为5,那么对应的圆锥的体积是多少?
【提示】(1)围成的圆锥如图所示:
(2)围成的圆锥的三视图如图所示:
(3)解:圆锥的高,
∴圆锥的体积
意图:本活动将展开图、实物图、三视图融为一体,并通过计算进一步沟通了三种图中线、面、体的对应转化关系.
(三)课堂练习
1.把如图中的纸片沿虚线折叠,可以围成一个几何体,这个几何体的名称是( A )
A.五棱锥 B.五棱柱 C.六棱锥 D.六棱柱
2.用马铃薯制成的立体模型,有四个面是全等的长方形,两个面是全等的正方形,长方形的宽等于正方形的边长,则这个立体模型的三视图是( A )
3.如图是某几何体的平面展开图,求图中圆的半径.
解:扇形的弧长,即底面(圆)的周长为
∴圆的半径为
意图:由于本节课实践操作要有充分的时间保障,所以课堂练习可以根据实际情况选用.
(四)课堂小结
教师提问:
1.本节课的课题学习中我们制作立体模型用了哪两种方法?分别经历哪几个步骤(方法)?
2.结合本节课的实践操作,谈一下你对三视图、展开图与立体模型之间关系,有什么新的认识?
在学生自由发言的基础上,与同伴进行交流,师生共同总结.
意图:鼓励学生根据自己的实践感受大胆发言,不追求共同答案.
(五)作业布置
A组:
1.一个几何体的三视图如图,用萝卜制作出它的立体模型的形状是( A )
2.要制作一个密封的长方体铁盒,嘉嘉设计出了它的三视图如图所示,按图中尺寸(单位:cm)判断,要制作这个长方体铁盒,如果只考虑面积因素,采用下列哪种面积的铁板最合理( C )
A.1 000 cm2 B.1 030 cm2 C.1 100 cm2 D.1 200 cm2
3.如图是一个食品包装盒的侧面展开图.
(1)请写出这个包装盒的多面体形状的名称;
(2)请根据图中所标的尺寸,计算这个多面体的侧面积和表面积.
解:(1)这个包装盒的多面体形状是六棱柱;
(2)侧面积为6ab,表面积为6ab+3b2.
B组:三视图和展开图都是与立体图形有关的平面图形,利用课余时间,结合我们的生活实际和具体的事例,写一篇短文介绍三视图、展开图的应用,以及你的感受.
效果:布置分层作业,照顾不同学情的学生,进行自我评估,数学短文的写作比较新颖,促进学生联系生活实际,对本章相关内容的梳理与表达.
六、板书设计
七、课后反思
本课时的课题学习放在全章的最后,设计了动手实践的活动,通过制作简单立体模型来加强对三视图等的理解认识.学习本章内容时,动脑活动与动手活动相结合是非常有效的,使学生经历观察、画图、想象、制作模型等认识过程是非常必要的.因此,在教学中对于本章安排的实践性较强的课题学习,要结合学生实际加以落实,而不要以教师的讲授代替学生的亲身体验.
1
一、教学内容分析
本节课安排的课题学习是观察、想象、制作相结合的实践活动,这是结合实际动脑与动手并重的学习内容.进行这个课题学习既可以采用独立完成的形式,也可以采用合作式学习的方式.应该把这个课题学习看作对前面学习的内容是否切实理解掌握以及能否灵活运用的一次联系实际的检验.
二、教学目标
1.根据三视图或展开图制作立体模型,进一步加深对投影和视图知识的认识.
2.在实际动手中进一步探索三视图、实物模型与展开图之间的关系,加强在实践活动中手脑结合的能力.
三、教学重难点
【重点】根据三视图或展开图制作出符合平面图形特征的立体模型.
【难点】在手工操作过程中,通过裁剪、折叠、拼接、削切等方法得到想象中的实物模型.
四、教学方法
操作演示法和合作探究法.鉴于本课时具有鲜明的综合与实践特点,并且对部分学生而言,把想象的物体通过动手操作制作成实物模型有一定挑战性,所以提倡学生在独立思考、尝试完成的前提下,开展合作学习,通过交流分享、质疑纠错、修订完善,完成学习任务.
五、教学过程
(一)课题准备
学习目的:通过由三视图制作立体模型的实践活动,体验平面图形向立体图形转化的过程,体会用三视图表示立体图形的作用,进一步感受立体图形与平面图形之间的联系.
操作工具:刻度尺、剪刀、小刀、胶水、硬纸板、马铃薯(或萝卜)等.
几点要求:
1.课题学习过程中,积极思考,由平面图形(三视图或展开图)想象立体图形的形状.
2.根据课题要求,通过裁剪、折叠、拼接、削切等方法制作实物模型.
3.解决与实物模型有关的数学问题.
4.操作过程中,工具的使用要符合规范,避免安全隐患.
5.学习过程中,首先尝试独立思考解决问题,然后进行合作交流,完善方案,分享成果.
意图:从目的、工具、要求三个方面为整节课的学习奠定总基调,特别强调独立操作与合作探究相结合,大胆操作与注意安全相结合.
(二)课题活动
活动一 用硬纸板制作立体模型
任务:以硬纸板为主要材料,分别做出下面的两组三视图(如图)表示的立体模型.
思考:
1. 由三视图可知这个立体图形是什么形状的?画图描述它的形状.
2.要用硬纸板围成立体模型,那么它的展开图形状是什么形状的?画出它的展开图.
3.在硬纸板上剪下展开图,怎样折叠能围成封闭的立体模型?
【提示】图(1)如下:
图(2)如下:
操作:根据要求,用硬纸板围成以上两个立体模型,使用剪刀时注意安全.
归纳:用硬纸板制作立体模型的一般方法:
①由三视图描述立体图形的形状;
②根据立体图形的形状画出表面展开图;
③在硬纸板上剪下展开图;
④折叠展开图,拼接围成立体模型.
意图:以上任务在教师的引导下,学生完成,使之经历由三视图到实物图,再到展开图,直至制作立体模型的全过程,在实际操作中,加深对相关图形转化与内在关系的认识.
活动二 用马铃薯制作实物模型
任务:按照下面给出的两组三视图,用马铃薯做出相应的实物模型.
(1) (2)
思考:由三视图可得这两个立体图形是什么形状的?画图描述.
【提示】如图所示:
(1) (2)
讨论:对照第一个课题学习任务,二者在“制作流程”上有哪些不同之处?
【提示】主要关注两点:
1.由于制作材料不同,所以这个任务的制作方法是削切刻制的方法,直接出来实物模型(实心的),而非围成的立体图形(空心的).
2.由于制作方法不同,所以制作过程中不用画展开图,而是根据实物图直接制作.
操作:根据要求,用马铃薯刻制以上两个实物模型,使用小刀时注意安全.
归纳:用马铃薯制作立体模型的一般方法:
①由三视图描述立体图形的形状;
②根据立体图形的形状,削切出马铃薯的大致轮廓;
③去掉多余部分,逐步调整,直至刻制出实物模型.
意图:与第一个任务进行比较,在此基础上以学生为主完成,使之经历由三视图到实物图,再到制作实物模型的全过程,在实际操作中,加深对三视图与实物模型之间的转化与内在关系的认识.
活动三 探索三棱锥模型
任务:如图,下面每一组平面图形都由四个等边三角形组成.
(1)其中哪些可以折叠成三棱锥?把图形描在纸上,剪下来,叠一叠,验证你的结论.
(2)画出由上面图形能折叠成的三棱锥的三视图,并指出三视图中是怎样体现“长对正,高平齐,宽相等”的.
(3)如果上图中小三角形的边长为1,那么对应的三棱锥的表面积是多少?
【提示】(1)图(1)(3)可以折叠成三棱锥.
(2)如图所示:
(3)∵,
∴.
意图:给学生更大的自主探索讨论空间,通过观察、思考、操作、对比、计算,感受三视图与立体图形在转化过程中的位置关系与数量关系.
活动四 探索圆锥模型
任务:如图所示的图形由一个扇形和一个圆组成.
(1)把图形描在纸上,剪下来,围成一个圆锥.
(2)画出由图形围成的圆锥的三视图.
(3)如果图中扇形的半径为13,圆的半径为5,那么对应的圆锥的体积是多少?
【提示】(1)围成的圆锥如图所示:
(2)围成的圆锥的三视图如图所示:
(3)解:圆锥的高,
∴圆锥的体积
意图:本活动将展开图、实物图、三视图融为一体,并通过计算进一步沟通了三种图中线、面、体的对应转化关系.
(三)课堂练习
1.把如图中的纸片沿虚线折叠,可以围成一个几何体,这个几何体的名称是( A )
A.五棱锥 B.五棱柱 C.六棱锥 D.六棱柱
2.用马铃薯制成的立体模型,有四个面是全等的长方形,两个面是全等的正方形,长方形的宽等于正方形的边长,则这个立体模型的三视图是( A )
3.如图是某几何体的平面展开图,求图中圆的半径.
解:扇形的弧长,即底面(圆)的周长为
∴圆的半径为
意图:由于本节课实践操作要有充分的时间保障,所以课堂练习可以根据实际情况选用.
(四)课堂小结
教师提问:
1.本节课的课题学习中我们制作立体模型用了哪两种方法?分别经历哪几个步骤(方法)?
2.结合本节课的实践操作,谈一下你对三视图、展开图与立体模型之间关系,有什么新的认识?
在学生自由发言的基础上,与同伴进行交流,师生共同总结.
意图:鼓励学生根据自己的实践感受大胆发言,不追求共同答案.
(五)作业布置
A组:
1.一个几何体的三视图如图,用萝卜制作出它的立体模型的形状是( A )
2.要制作一个密封的长方体铁盒,嘉嘉设计出了它的三视图如图所示,按图中尺寸(单位:cm)判断,要制作这个长方体铁盒,如果只考虑面积因素,采用下列哪种面积的铁板最合理( C )
A.1 000 cm2 B.1 030 cm2 C.1 100 cm2 D.1 200 cm2
3.如图是一个食品包装盒的侧面展开图.
(1)请写出这个包装盒的多面体形状的名称;
(2)请根据图中所标的尺寸,计算这个多面体的侧面积和表面积.
解:(1)这个包装盒的多面体形状是六棱柱;
(2)侧面积为6ab,表面积为6ab+3b2.
B组:三视图和展开图都是与立体图形有关的平面图形,利用课余时间,结合我们的生活实际和具体的事例,写一篇短文介绍三视图、展开图的应用,以及你的感受.
效果:布置分层作业,照顾不同学情的学生,进行自我评估,数学短文的写作比较新颖,促进学生联系生活实际,对本章相关内容的梳理与表达.
六、板书设计
七、课后反思
本课时的课题学习放在全章的最后,设计了动手实践的活动,通过制作简单立体模型来加强对三视图等的理解认识.学习本章内容时,动脑活动与动手活动相结合是非常有效的,使学生经历观察、画图、想象、制作模型等认识过程是非常必要的.因此,在教学中对于本章安排的实践性较强的课题学习,要结合学生实际加以落实,而不要以教师的讲授代替学生的亲身体验.
1
