初中数学人教版八上15.3分式方程 第1课时 习题(含解析)
文档属性
| 名称 | 初中数学人教版八上15.3分式方程 第1课时 习题(含解析) |

|
|
| 格式 | docx | ||
| 文件大小 | 295.0KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-09-13 07:56:14 | ||
图片预览


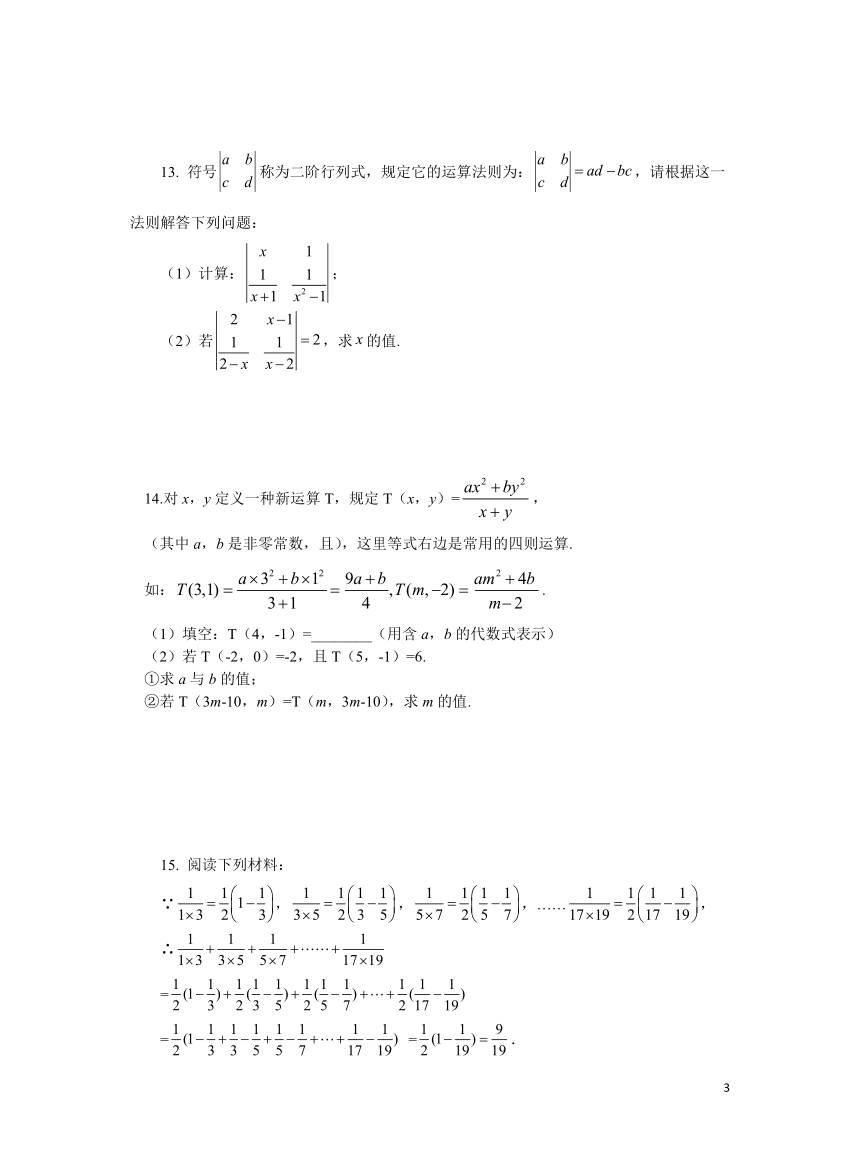

文档简介
15.3 分式方程 第1课时
1. 下列各式中,不是分式方程的是
A. B.
C. D.
2.下列分式方程去分母后所得结果正确的是
A.去分母得,
B.去分母得,
C.去分母得,
D.去分母得,
3.x=2是分式方程的解,则a的值是
A.-1 B.0 C.1 D.3
4. 我国古代著作《四元玉鉴》记载“买椽多少”问题:“六贯二百一十钱,请人去买几株椽.每株脚钱三文足,无钱准与一株椽.”其大意为:现请人代买一批椽,这批椽的价钱为6210文.如果每株椽的运费是3文,那么少拿一株椽后,剩下的椽的运费恰好等于一株椽的价钱,试问6210文能买多少株椽?设这批椽的数量为株,则符合题意的方程是
A. B. C. D.
5.若关于的分式方程无解,则的值为
A. B.0 C.3 D.0或3
6. 若关于的不等式组无解,且关于的分式方程的解为非负整数,则符合条件的所有整数的和为
A.6 B.16 C.18 D.20
7. 若a使关于x的不等式组有且只有四个整数解,且使关于y的方程的解为非负数,则符合题意的所有整数α的个数为 .
8. 某校为满足学生参加中考体育考试的需求,计划购买--定数量的篮球和足球.若每个足球的价格比篮球的价格贵25元,且用800元购买篮球的数量与用1000元购买足球的数量相同.设每个足球的价格为元,则可列方程为 .
9. 若关于x的分式方程的解是非负数,则a的取值范围为 .
10. 已知分式方程有增根,求m的值.
11.解方程:
(1) (2)
12. 解方程:.
佳佳的解题过程如下:
解:去分母,得.①
合并同类项,得.②
系数化为1,得.③
检验:当时,,
∴原分式方程的解为,请问佳佳的解题过程从哪一步开始出错?并将正确的解题过程写出来.
13. 符号称为二阶行列式,规定它的运算法则为:,请根据这一法则解答下列问题:
(1)计算:;
(2)若,求的值.
14.对x,y定义一种新运算T,规定T(x,y)=,
(其中a,b是非零常数,且),这里等式右边是常用的四则运算.
如:.
(1)填空:T(4,-1)=________(用含a,b的代数式表示)
(2)若T(-2,0)=-2,且T(5,-1)=6.
①求a与b的值;
②若T(3m-10,m)=T(m,3m-10),求m的值.
15. 阅读下列材料:
∵,,,……,
∴
=
= =.
解答下列问题:
(1)在和式中,第6项为______,第n项是__________.
(2)上述求和的想法是通过逆用________法则,将和式中的各分数转化为两个数之差,使得除首末两项外的中间各项可以_______,从而达到求和的目的.
(3)受此启发,请你解下面的方程:
.
参考答案
1.D
解析:A,B,C方程中分母中都含有字母,都是分式方程,
D,方程分母中不含未知数,所以不是分式方程.
2.D
解析:A,去分母得:,不符合题意;
B,去分母得:,不符合题意;
C,去分母得:,不符合题意;
D,去分母得:,符合题意.
3.D
解析:是分式方程的解,,解得a=3.经检验,a=3是的解.
4. A.
解析:根据单价总价数量,结合少拿一株椽后剩下的椽的运费恰好等于一株椽的价钱,即可得出关于的分式方程, .
5. A
解:,
方程两边同时乘以,得,
去括号得,,
移项、合并同类项得,,
方程无解,
,
,
.
6.B
解析:∵=1﹣,解得:且,
∵关于y的分式方程=1﹣的解为非负整数,
∴≥0且,即:a≥-2且a≠4,
∵,
∴,
∵关于x的不等式组无解,
∴,即:,
∴且a≠4,
∵是非负整数,
∴,,,
∴符合条件的所有整数a的和为:-2+1+7+10=16.
7. 3个
解析:不等式组整理得:,
由不等式组有且只有四个整数解,得到,
解得:,即整数,0,1,2,
分式方程去分母得:,
解得:,
,
,
,
由分式方程的解为非负数以及分式有意义的条件,得到为,0,2共3个.
8.
解:设每个足球的价格为元,则每个篮球(x-25)元,
根据题意得,
9. a≥1且a≠3
解析:∵,
∴3(x+a)﹣6a=x﹣3,
整理,可得:2x=3a﹣3,
解得:x=,
∵关于x的分式方程的解是非负数,
∴≥0,且≠3,
解得:a≥1且a≠3.
10.解:去分母得:x+x﹣3=﹣5m,
由分式方程有增根,得到x﹣3=0,即x=3,
把x=3代入整式方程得:3+3﹣3=﹣5m,
解得:m=﹣0.6.
11. 解:(1)
两边同乘,得:,
去括号,得:,
移项,得:,
合并同类项,得:,
系数化为1,得:,
经检验,为分式方程的解.
(2)
同时乘,得:,
去括号,得:,
移项,合并同类项,得:,
系数化为1,得:,
经检验:是分式方程的增根,原分式方程无解.
12. 解:佳佳的解题过程从第①步开始出错,正确的解题过程如下:
去分母,得.
移项、合并同类项,得.
检验:当时,,∴原分式方程的解为.
13.解: (1)原式
;
(2)根据题意得:
解之得:
经检验:是原分式方程的解
所以的值为5.
14. 解:(1).
(2)①,且T(5,-1)=6,,解得.
②解法一:
∵a=1,b=-1,且,
,
,
.
解得m=5.
解法二:由解法一可知,
当时,
.
.
15. 解:(1)根据题中的规律可得:;
(2)分式减法,对消;
(3)解析:将分式方程变形为,
整理得,
方程两边都乘以2x(x+9),得
2(x+9)-2x=9x,解得x=2.
经检验,x=2是原分式方程的根.
1
1. 下列各式中,不是分式方程的是
A. B.
C. D.
2.下列分式方程去分母后所得结果正确的是
A.去分母得,
B.去分母得,
C.去分母得,
D.去分母得,
3.x=2是分式方程的解,则a的值是
A.-1 B.0 C.1 D.3
4. 我国古代著作《四元玉鉴》记载“买椽多少”问题:“六贯二百一十钱,请人去买几株椽.每株脚钱三文足,无钱准与一株椽.”其大意为:现请人代买一批椽,这批椽的价钱为6210文.如果每株椽的运费是3文,那么少拿一株椽后,剩下的椽的运费恰好等于一株椽的价钱,试问6210文能买多少株椽?设这批椽的数量为株,则符合题意的方程是
A. B. C. D.
5.若关于的分式方程无解,则的值为
A. B.0 C.3 D.0或3
6. 若关于的不等式组无解,且关于的分式方程的解为非负整数,则符合条件的所有整数的和为
A.6 B.16 C.18 D.20
7. 若a使关于x的不等式组有且只有四个整数解,且使关于y的方程的解为非负数,则符合题意的所有整数α的个数为 .
8. 某校为满足学生参加中考体育考试的需求,计划购买--定数量的篮球和足球.若每个足球的价格比篮球的价格贵25元,且用800元购买篮球的数量与用1000元购买足球的数量相同.设每个足球的价格为元,则可列方程为 .
9. 若关于x的分式方程的解是非负数,则a的取值范围为 .
10. 已知分式方程有增根,求m的值.
11.解方程:
(1) (2)
12. 解方程:.
佳佳的解题过程如下:
解:去分母,得.①
合并同类项,得.②
系数化为1,得.③
检验:当时,,
∴原分式方程的解为,请问佳佳的解题过程从哪一步开始出错?并将正确的解题过程写出来.
13. 符号称为二阶行列式,规定它的运算法则为:,请根据这一法则解答下列问题:
(1)计算:;
(2)若,求的值.
14.对x,y定义一种新运算T,规定T(x,y)=,
(其中a,b是非零常数,且),这里等式右边是常用的四则运算.
如:.
(1)填空:T(4,-1)=________(用含a,b的代数式表示)
(2)若T(-2,0)=-2,且T(5,-1)=6.
①求a与b的值;
②若T(3m-10,m)=T(m,3m-10),求m的值.
15. 阅读下列材料:
∵,,,……,
∴
=
= =.
解答下列问题:
(1)在和式中,第6项为______,第n项是__________.
(2)上述求和的想法是通过逆用________法则,将和式中的各分数转化为两个数之差,使得除首末两项外的中间各项可以_______,从而达到求和的目的.
(3)受此启发,请你解下面的方程:
.
参考答案
1.D
解析:A,B,C方程中分母中都含有字母,都是分式方程,
D,方程分母中不含未知数,所以不是分式方程.
2.D
解析:A,去分母得:,不符合题意;
B,去分母得:,不符合题意;
C,去分母得:,不符合题意;
D,去分母得:,符合题意.
3.D
解析:是分式方程的解,,解得a=3.经检验,a=3是的解.
4. A.
解析:根据单价总价数量,结合少拿一株椽后剩下的椽的运费恰好等于一株椽的价钱,即可得出关于的分式方程, .
5. A
解:,
方程两边同时乘以,得,
去括号得,,
移项、合并同类项得,,
方程无解,
,
,
.
6.B
解析:∵=1﹣,解得:且,
∵关于y的分式方程=1﹣的解为非负整数,
∴≥0且,即:a≥-2且a≠4,
∵,
∴,
∵关于x的不等式组无解,
∴,即:,
∴且a≠4,
∵是非负整数,
∴,,,
∴符合条件的所有整数a的和为:-2+1+7+10=16.
7. 3个
解析:不等式组整理得:,
由不等式组有且只有四个整数解,得到,
解得:,即整数,0,1,2,
分式方程去分母得:,
解得:,
,
,
,
由分式方程的解为非负数以及分式有意义的条件,得到为,0,2共3个.
8.
解:设每个足球的价格为元,则每个篮球(x-25)元,
根据题意得,
9. a≥1且a≠3
解析:∵,
∴3(x+a)﹣6a=x﹣3,
整理,可得:2x=3a﹣3,
解得:x=,
∵关于x的分式方程的解是非负数,
∴≥0,且≠3,
解得:a≥1且a≠3.
10.解:去分母得:x+x﹣3=﹣5m,
由分式方程有增根,得到x﹣3=0,即x=3,
把x=3代入整式方程得:3+3﹣3=﹣5m,
解得:m=﹣0.6.
11. 解:(1)
两边同乘,得:,
去括号,得:,
移项,得:,
合并同类项,得:,
系数化为1,得:,
经检验,为分式方程的解.
(2)
同时乘,得:,
去括号,得:,
移项,合并同类项,得:,
系数化为1,得:,
经检验:是分式方程的增根,原分式方程无解.
12. 解:佳佳的解题过程从第①步开始出错,正确的解题过程如下:
去分母,得.
移项、合并同类项,得.
检验:当时,,∴原分式方程的解为.
13.解: (1)原式
;
(2)根据题意得:
解之得:
经检验:是原分式方程的解
所以的值为5.
14. 解:(1).
(2)①,且T(5,-1)=6,,解得.
②解法一:
∵a=1,b=-1,且,
,
,
.
解得m=5.
解法二:由解法一可知,
当时,
.
.
15. 解:(1)根据题中的规律可得:;
(2)分式减法,对消;
(3)解析:将分式方程变形为,
整理得,
方程两边都乘以2x(x+9),得
2(x+9)-2x=9x,解得x=2.
经检验,x=2是原分式方程的根.
1
