【全程复习方略】2014-2015学年高中数学理(人教广东版)教师配套课件选修4-1第二节直线与圆的位置关系(共101张PPT)
文档属性
| 名称 | 【全程复习方略】2014-2015学年高中数学理(人教广东版)教师配套课件选修4-1第二节直线与圆的位置关系(共101张PPT) |

|
|
| 格式 | zip | ||
| 文件大小 | 2.3MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教新课标A版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2014-12-26 11:26:11 | ||
图片预览









文档简介
课件101张PPT。第二节 直线与圆的位置关系1.圆周角和圆心角定理
(1)圆周角定理:圆上一条弧所对的圆周角等于它所对的
_______的一半.
(2)圆心角定理:圆心角的度数等于_________的度数.
推论1:同弧或等弧所对的_______相等;同圆或等圆中,相等
的圆周角所对的___也相等.
推论2:半圆(或直径)所对的圆周角是_____;90°的圆周角所
对的弦是_____.圆心角它所对弧圆周角弧直角直径2.圆的内接四边形的性质与判定定理
定理1:圆的内接四边形的对角_____.
定理2:圆内接四边形的外角等于
它的___________.
定理:如果一个四边形的对角互补,
那么这个四边形的四个顶点_____.
推论:如果四边形的一个外角等于它的
内角的对角,那么这个四边形的四个
顶点共圆.互补内角的对角共圆3.圆的切线的性质与判定及弦切角定理
(1)圆的切线的性质与判定.
性质定理:圆的切线垂直于经过切点的_____.
推论1:经过圆心且垂直于切线的直线必经过_____.
推论2:经过切点且垂直于切线的直线必经过_____.
判定定理:经过半径的外端并且_____于这条半径的直线是圆
的切线.
(2)弦切角定理.
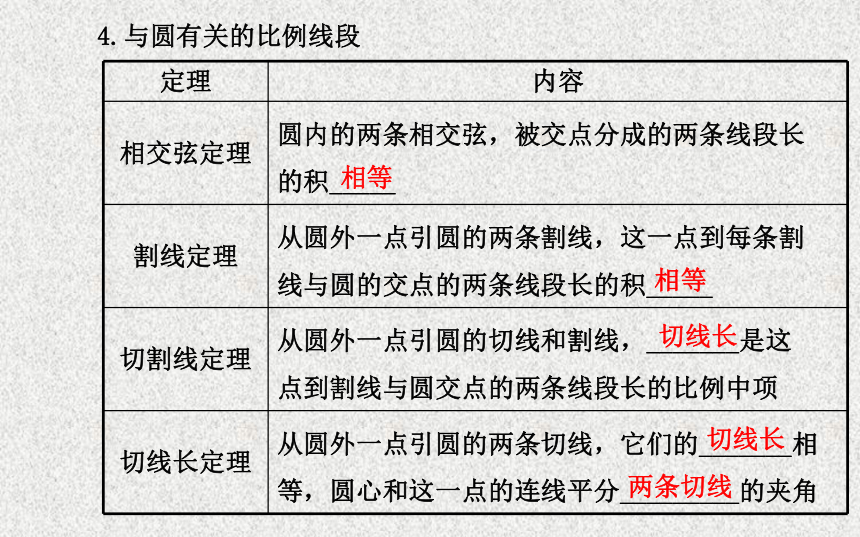
弦切角等于它所夹的弧所对的_______.半径切点圆心垂直圆周角4.与圆有关的比例线段相等相等切线长切线长两条切线判断下面结论是否正确(请在括号中打“√”或“×”).
(1)圆心角等于圆周角的2倍.( )
(2)相等的圆周角所对的弧也相等.( )
(3)任意一个四边形、三角形都有外接圆.( )
(4)等腰梯形一定有外接圆.( )
(5)弦切角所夹弧的度数等于弦切角的度数.( )【解析】(1)错误,若弧不一样,则圆心角与圆周角的关系不确定.
(2)错误,只有同圆或等圆中,相等的圆周角所对的弧才相等.
(3)错误,任意一个四边形不一定有外接圆,但任意一个三角形一定有外接圆.
(4)正确, 可以推出等腰梯形的对角互补,所以有外接圆.(5)错误,弦切角等于它所夹的弧所对的圆周角,所夹的弧的度数等于该弧所对圆心角的度数,所以弦切角所夹弧的度数等于弦切角度数的2倍.
答案:(1)× (2)× (3)× (4)√ (5)×考向 1 圆周角定理
【典例1】(1)(2013·中山模拟)如图,AB为⊙O的直径,弦
AC,BD交于点P,若AB=3,CD=1,则sin∠CBD=____.
(2)(2013·汕头模拟)点A,B,C是圆O上的点,且AB=2,BC=
∠CAB= 则∠ABC=____.【思路点拨】(1)连接AD,结合圆周角定理、正弦定理得到
再利用AD=ABsin∠ABD求解.
(2)连接CO,把∠CAB= 转化为∠BOC= 利用等腰三角形
BOC求出半径,可得△AOB为等腰直角三角形,再利用圆周角定
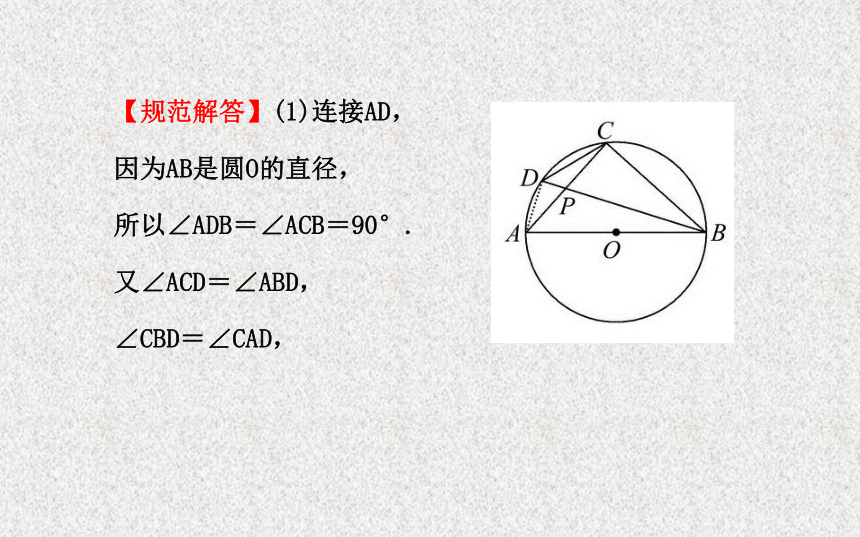
理转化即可.【规范解答】(1)连接AD,
因为AB是圆O的直径,
所以∠ADB=∠ACB=90°.
又∠ACD=∠ABD,
∠CBD=∠CAD,所以在△ACD中,
由正弦定理得:
= =AB=3,又CD=1,
所以sin∠CAD= 又∠CBD=∠CAD,
所以sin∠CBD=
答案:(2)连接CO,因为∠CAB= 所
以优弧BC所对的圆心角为
从而∠BOC= 在等腰三角形
BOC中可求得半径OB= 因为AB
=2,所以△AOB为等腰直角三角
形,所以∠AOB= 所以
∠AOC= ,∠ABC= ∠AOC= .
答案:【拓展提升】圆周角定理常用的三种转化
(1)圆周角与圆周角之间的转化.
(2)圆周角与圆心角之间的转化.
(3)弧的度数与圆心角和圆周角之间的转化.【变式训练】(1)如图所示,圆的内接三角形ABC的角平分线BD与AC交于点D,与圆交于点E,连接AE,已知ED=3,BD=6,则线段AE的长=____.【解析】∵∠E=∠E,BE平分∠ABC,∠EAD=∠EBC,所以
∠EAD=∠EBA,∴△EDA∽△EAB,
∴ 即AE2=ED·BE=3×9=27,
∴AE=
答案:(2)如图,已知PA,PB是圆O的切线,A,B分别为切点,C为圆O上不与A,B重合的另一点,若∠ACB = 120°,则∠APB =____.【解析】如图所示,连接OA,OB, ∵∠ACB =120°.
∴优弧AB所对的圆心角为240°,从而∠AOB=120°.
又PA,PB是圆O的切线,
∴∠OAP=∠OBP=90°,∴∠APB=60°.
答案:60°考向 2 圆内接四边形的判定与性质
【典例2】(1)如图所示,在梯形ABCD中,AD∥BC,点E,F分别
在边AB,CD上,设ED与AF相交于点G,若B,C,F,E四点共
圆.且AG=1,GF=2,DG= 则GE=____.(2)如图所示,已知AP是⊙O的切线,P为切点,AC是⊙O的割线,与⊙O交于B,C两点,圆心O在∠PAC的内部,点M是BC的中点.若∠OAM=25°,则∠APM =____.【思路点拨】(1)连接EF,由AD∥BC及B,C,F,E四点共圆,可判断A,D,F,E四点共圆,再利用相交弦定理求GE.(2)连接OP,OM,可证 A,P,O,M四点共圆,由∠OAM=∠OPM即可求解.【规范解答】(1)如图所示,
连接EF.
∵B,C,F,E四点共圆,
∴∠ABC=∠EFD.
∵AD∥BC,
∴∠BAD+∠ABC=180°.
∴∠BAD+∠EFD=180°.∴A,D,F,E四点共圆.
由相交弦定理,
可得AG·GF=DG·GE.
因此
答案:(2)连接OP,OM.
∵AP与⊙O相切于点P,
∴OP⊥AP.
∵M是⊙O的弦BC的中点,
∴OM⊥BC,
∴∠OPA+∠OMA=180°,∴A,P,O,M四点共圆.
∴∠OAM=∠OPM =25°,
∴∠APM=90°-25°=65°.
答案:65°【拓展提升】圆内接四边形的重要结论
(1)内接于圆的平行四边形是矩形.
(2)内接于圆的菱形是正方形.
(3)内接于圆的梯形是等腰梯形.【变式训练】(2013·广州模拟)如图,⊙O中,直径AB和弦DE互相垂直,C是DE延长线上一点,连接BC与圆O交于F,若∠CFE=40°,则∠DEB=____.【解析】∵AB⊥DE,∴∠BDE=∠DEB,根据圆的内接四边形性质定理,∠BDE=∠CFE,∴∠DEB=∠CFE=40°.
答案:40°考向 3 圆的切线的性质与判定、弦切角定理
【典例3】(1)(2012·广东高考)如图,圆O的半径为1,A,B,C是圆周上的三点,满足∠ABC=30°,过点A作圆O的切线与OC的延长线交于点P,则PA=____.
(2)如图所示,AB是⊙O的直径,⊙O过BC的中点D,DE⊥AC.若∠ADE=50°,则∠ABD=____.【思路点拨】(1)连接OA,AC从而可得△AOC为等边三角形,∠PAC=30°,△PAC为等腰三角形,再由AC=CP=1可得结果.
(2)连接OD,证明DE是圆O的切线,再利用弦切角定理进行转化即可.【规范解答】(1)连接AO,AC,因为
∠ABC=30°,
∴∠CAP=30°,
∠AOC=60°.
又∵OA=OC,
∴△AOC为等边三角形,则∠ACP=120°,
∴∠APC=30°,∴△ACP为等腰三角形,
且AC=CP=1,∴AP=2×1×sin 60°=
答案:(2)连接OD.∵BD=CD,OA=OB,
∴OD是△ABC的中位线,
∴OD∥AC.
又∵∠DEC=90°,
∴∠ODE=90°.
又∵D在圆周上,
∴DE是⊙O的切线.
因此∠ABD=∠ADE=50°.
答案:50°【互动探究】若例(2)条件不变,则∠BAC=____.
【解析】∵OD⊥DE,∠ADE=50°,∴∠ADO=40°.
∵OD=OA,∴∠DAO=∠ADO=40°.∵OD∥AE,
∴∠DAE=∠ADO=40°,∴∠BAC=∠DAE+∠DAO=40°+40°=80°.
答案:80°【拓展提升】证明直线是圆的切线的常用方法
(1)若已知直线与圆有公共点,则需证明圆心与公共点的连线垂直于已知直线即可.
(2)若已知直线与圆没有明确的公共点,则需证明圆心到直线的距离等于圆的半径.
【提醒】在求解有关角与长度的问题时,注意运用初中阶段所学的知识,如平行线的判定与性质、中垂线的性质、等腰三角形的三线合一、直角三角形的性质等,只有这样才能更灵活地解决问题.【变式备选】(1)如图所示,AB为⊙O的直径,C为⊙O上一点,AD和过C点的切线互相垂直,垂足为D.若∠BAC=35°,则∠CAD=____.【解析】连接OC.
∵CD是⊙O的切线,∴OC⊥CD.
又∵AD⊥CD,∴OC∥AD.由此得∠ACO=∠CAD.
∵OC=OA,∴∠BAC=∠ACO.
∴∠CAD=∠BAC.又∠BAC=35°,
故∠CAD=35°.
答案:35°(2)(2013·湛江模拟)如图,已知PA是圆O的切线,切点为A,直线PO交圆O于B,C两点,AC=2,∠PAB=120°,则圆O的面积为____. 【解析】由题意知∠BAC=90°,则∠PAC=120°-90°=30°.
由弦切角定理知,∠B=30°,∴BC=2AC=4,∴圆O的面积
S=4π.
答案:4π考向 4 与圆有关的比例线段
【典例4】(1)(2012·天津高考)如图,已知AB和AC是圆的两条
弦,过点B作圆的切线与AC的延长线相交于点D,过点C作BD的
平行线与圆相交于点E,与AB相交于点F,AF=3,FB=1,EF=
则线段CD的长为____.(2)如图,△ABC是⊙O的内接三角形,PA是⊙O的切线,PB交AC于点E,交⊙O于点D.若PA=PE,∠ABC=60°,PD=1,PB=9,则PA=____,EC=_____.【思路点拨】(1)利用相交弦定理求CF,再利用切割线定理和比例线段有关知识列方程求解.
(2)利用切割线定理求PA的长度,再判断△PAE为等边三角形,最后用相交弦定理求EC.【规范解答】(1)因为AF·FB=CF·FE,所以CF=2,
又∵ ∴BD=
∵CF∥BD,∴
设CD=x,则AD=4x,∴BD2=x·4x,∴x= .
答案:(2)由切割线定理可知PA2=PD·PB=1×9,
∴PA=3.∵∠ABC=∠PAC=60°,PA=PE,
∴△APE为等边三角形,
∴AE=AP=3,∵PD=1,
∴ED=PE-PD=2,BE=PB-PE=6,
由相交弦定理可知:
AE·EC=BE·ED,∴3·EC=6×2,∴EC=4.
答案:3 4【互动探究】在本例(1)中,若把条件“EF= ”改为“EF=2”,则AD=____.
【解析】设CD=x,则AD=4x,由相交弦定理可得,
AF·FB=EF·CF,所以CF= ,
又∵ ∴BD=2,
又BD2=CD·AD,
所以4=4x2,x=1,所以AD=4.
答案:4【拓展提升】与圆有关的比例线段解题思路
见到圆的两条相交弦就要想到相交弦定理;见到圆的两条割线就要想到割线定理;见到圆的切线和割线就要想到切割线定理.
【提醒】与圆有关的比例线段问题,常常结合方程思想进行计算,即利用代数方法解决几何问题.【变式备选】如图所示,已知P是⊙O外一点,PD为⊙O的切
线,D为切点,割线PEF经过圆心O,若PF=12,PD= 则
∠EFD的度数为____.【解析】由切割线定理得PD2=PE·PF?PE=
=4?EF=8,OD=4.
∵OD⊥PD,OD= PO,∴∠P=30°.
∴∠POD=60°,∠EFD=30°.
答案:30°1.如图所示,AB,AC是⊙O的两条切线,切点分别为B,C,D是优弧BC上的点,已知∠BAC=80°, 那么∠BDC=____.【解析】连接OB,OC,则OB⊥AB,OC⊥AC,
∴∠BOC=180°-∠BAC=100°,
∴∠BDC= ∠BOC=50°.
答案:50°2.(2013·广州模拟)如图所示,过点D作圆的切线切于B点,作割线交圆于A,C两点,其中BD=3,AD=4,AB=2,则BC=___.【解析】由切割线定理得:BD2=CD·AD,∴CD=
又∵∠A=∠DBC,∠D=∠D,∴△ABD∽△BCD,
∴ 解得BC=
答案:3.如图所示,AB,CD是半径为a的圆O的两条弦,它们相交于AB的中点P,PD= ∠OAP=30°,则CP=____.【解析】由题意知OP⊥AB,且AP=BP=
根据相交弦定理得AP2=CP·PD,∴CP= .
答案:4.(2012·湖北高考)如图,点D在⊙O的弦AB上移动,AB=4,连接OD,过点D作OD的垂线交⊙O于点C,则CD的最大值为____.【解析】取AB的中点为E,连接OC,OE,则
= 要求CD的最大值,则点D与E重合.可知结果
为2.
答案:25.如图所示,AC为⊙O的直径,弦BD⊥AC于点P,PC=2,PA=8,则cos∠ACB的值为____.【解析】∵AC是直径,
∴∠ABC=90° ,
又BD⊥AC,
BC2=PC·AC=2×10,
∴BC=
在Rt△BPC中,cos∠ACB=
答案:6. (2013·汕头模拟)如图所示,正△ABC的边长为2,点M,N分别是边AB,AC的中点,直线MN与△ABC的外接圆的交点为P,Q,则线段PM=____.【解析】设PM=x,则QN=x,由相交弦定理可得PM·MQ=
BM·MA,
即x·(x+1)=1,解得
答案:7.如图所示,BD为⊙O的直径,AB=AC,AD交BC于E,AE=2,ED=4.则AB的长为____.【解析】∵AB=AC,∴∠ABC=∠C,
又∵∠C=∠D,∴∠ABC=∠D,又∠BAE=∠DAB,
∴△ABE∽△ADB,
∴AB2=AE·AD,∴AB=
答案:8.(2012·陕西高考)如图所示,在圆O中,直径AB与弦CD垂直,垂足为E,EF⊥DB,垂足为F ,若AB=6,AE=1,则DF·DB=____.【解析】连接AD,因为AB=6,AE=1,所以BE=5, 在Rt△ABD中,DE2=AE·BE=1×5=5,在Rt△BDE中,由射影定理得DF·DB=DE2=5.
答案:59.如图所示,AD是⊙O的切线,AC是⊙O的弦,过C作AD的垂线,垂足为B,CB与⊙O相交于点E,AE平分∠CAB,且AE=2,则AB=_____,AC=_____. 【解析】∵∠CAE=∠EAB,∠EAB=∠ACB,
∴∠ACB=∠CAE=∠EAB.又∵CB⊥AD,
∴∠ACB=∠CAE=∠EAB=30°.
又∵AE=2,∴AB= AC=
答案:10.如图所示,已知圆上的 过C点的圆的切线与BA的延长线交于E点,若∠ACE=35°,则∠BCD=____.【解析】因为 所以∠ABC=∠BCD.又因为EC与圆相切于点C,
故∠ACE=∠ABC.所以∠ACE=∠BCD.
又∠ACE=35°,因此∠BCD=35°.
答案:35°11.如图所示,四边形ABCD是圆O的内接四边形,延长AB和DC相
交于点P,若 则 的值为_____.【解析】由割线定理知:PB·PA=PC·PD,
又∵PA=2PB,PD=3PC,
∴PB·2PB= PD·PD,
∴PB2= PD2,∴PB= PD.
又∵△PBC∽△PDA,
∴
答案:12.如图所示,在△ABC中,AD是高,△ABC的外接圆直径AE交BC边于点G,有下列结论:
①AD2=BD·CD;②BE2=EG·AE;③AE·AD=AB·AC;
④AG·EG=BG·CG.其中正确的结论有____.【解析】①中仅当∠BAC为直角时才成立;②中仅当BG⊥AE时
才成立;因为∠AEB=∠ACD,∠ABE=∠ADC,所以
△AEB∽△ACD,故 即AE·AD=AB·AC,故③正确;
由相交弦定理知④正确.
答案:③④13.(2012·广东高考)如图所示,直线PB与圆O相切于点B,D是弦AC上的点,∠PBA=∠DBA.若AD=m,AC=n,则AB=____.【解析】由题意知∠ABP=∠ACB=∠ABD,
又∠A=∠A,所以△ABD∽△ACB,
所以
所以AB= =
答案:14.如图所示,四边形ABCD内接于⊙O,BC是直径,MN与⊙O相切,切点为A,∠MAB=35°,则∠ADC=____.【解析】连接BD,
由题意知,∠ADB=∠MAB=35°,∠BDC=90°,故∠ADC=∠ADB+∠BDC=125°.
答案:125°15.EB,EC是⊙O的两条切线,B,C是切点,A,D是⊙O上的两点,如果∠E=46°,∠DCF=32°,那么∠BAD=_____.【解析】连接OB,OC,AC,
根据弦切角定理,可得∠BAD=∠BAC+∠CAD=
(180°-∠E)+∠DCF=67°+32°=99°.
答案:99°16.如图所示,AB是⊙O的直径,CB切⊙O于点B,CD切⊙O于点D,直线CD交直线AB于点E.若AB=3,ED=2,则CB的长为___.【解析】由切割线定理得,ED2=EA·EB,
∴4=EA(EA+3),
∴EA=1.∵CB是⊙O的切线,∴EB⊥CB,
∴EB2+CB2=CE2.
又∵CD是⊙O的切线,∴CD=CB,
∴42+CB2=(CB+2)2,∴CB=3.
答案:317.如图所示,AB为⊙O的直径,C为⊙O上一点,AP和过C的切线互相垂直,垂足为P,过B的切线交过C的切线于T,PB交⊙O于Q,若∠BTC=120°,AB=4,则PQ·PB=____.【解析】连接OC,AC,则OC⊥PC,则O,C,T,B四点共圆,
∵∠BTC=120°,∴∠COB=60°,
故∠AOC=120°.
由AO=OC=2,知AC=
在Rt△APC中,∠ACP=60°,
因此PC=
根据切割线定理得PQ·PB=PC2=3.
答案:318.(2013·佛山模拟)如图所示,AB是⊙O的直径,D为⊙O上一点,过D作⊙O的切线交AB的延长线于点C,若DA=DC,且BC=5,则AB=____.【解析】如图所示,连接OD,∵CD是⊙O的切线,
∴∠ODC=90°.
设∠C=θ,则∠A=θ,∠ADO=θ.∵θ+θ+θ+90°=180°,∴θ=30°,
∴OC=2OD.
设圆O的半径为r,则OC=2r,∴BC=r.
∴AB=2BC=10.
答案:1019.如图所示,已知⊙O的直径AB=5,C为圆周上一点,BC=4,过点C作⊙O的切线l,过点A作l的垂线AD,垂足为D,则CD=____.【解析】∵CD是⊙O的切线,
∴∠B=∠ACD,
又AB为直径,∴∠ACB=∠ADC=90°,
∴△ABC∽△ACD,∴
∵AB=5,BC=4,∴AC=3,∴CD=
答案:20.如图所示,割线PBC经过圆心O,OB=PB=1,OB绕点O逆时针旋转120°到OD,连接PD交圆O于点E,则PE=____.【解析】依题意得,
PD=
又PE·PD=PB·PC,
因此PE=
答案:21.Rt△ABC中,∠C=90°,∠A=30°,圆O经过B,C且与
AB,AC相交于D,E.若AE=EC= 则AD=___,圆O的半径
r=____.【解析】在Rt△ABC中,∠BAC=30°,AC= 所以BC=4,
AB=8,由割线定理得AE·AC=AD·AB,所以AD=
因为∠C=90°,连接BE,则BE是圆O的直
径.所以 所以圆O的半径r= .
答案:3 22.如图所示,A,E是半圆周上的两个三等分点,直径BC=4,AD⊥BC,垂足为D,BE与AD相交于点F,则AF的长为_____.【解析】如图,连接CE,AO,AB.根据A,E是半圆周上的两个三等分点,BC为直径,可得∠CEB=90°,∠CBE=30°,∠AOB=60°,故△AOB为等边三角形,AD=
OD=BD=1,∴DF=
∴AF=AD-DF=
答案:23.已知EB是半圆O的直径,A是BE延长线上一点,AC切半圆O于点D,BC⊥AC于点C,若BC=6,AC=8,则AE=____,
AD=____.【解析】∵OD⊥AC,BC⊥AC,
∴△ADO∽△ACB,∴
∵BC=6,AC=8,∴AB=10,
设OD=R,则AO= R,∴R+ R=10,∴R=
AE=AB-2R= , ∴AD=5.
答案: 524.如图所示,过圆C外一点P作一条直线与圆C交于A,B两点,AB=2AP,PT与圆C相切于T点.已知圆C的半径为2,∠CAB=30°,则PT=_____.【解析】∵AC=2,∠CAB=30°,
∴AB=2ACcos 30°=2×2× =
∴AP= AB= ∴PB=AP+AB=
∵PT是⊙C的切线,∴PT2=AP·PB=9,
∴PT=3.
答案:325.如图所示,已知⊙O1与⊙O2相交于A,B两点,过点B作两圆的割线,分别交⊙O1,⊙O2于点D,E.过E作CE∥AD交⊙O2于C,连AC交DE于点P. 若AD是⊙O2的切线,且PA=6,PC=2,BD=9,则AD的长为_____.【解析】设BP=x,PE=y.
∵PA=6,PC=2,
∴由相交弦定理得PA·PC=BP·PE,即xy=12①,
∵AD∥CE,∴ ∴ ②,
由①②可得,∴DE=9+x+y=16.
∵AD是⊙O2的切线,DE是⊙O2的割线,
∴AD2=BD·DE=9×16,∴AD=12.
答案:12
(1)圆周角定理:圆上一条弧所对的圆周角等于它所对的
_______的一半.
(2)圆心角定理:圆心角的度数等于_________的度数.
推论1:同弧或等弧所对的_______相等;同圆或等圆中,相等
的圆周角所对的___也相等.
推论2:半圆(或直径)所对的圆周角是_____;90°的圆周角所
对的弦是_____.圆心角它所对弧圆周角弧直角直径2.圆的内接四边形的性质与判定定理
定理1:圆的内接四边形的对角_____.
定理2:圆内接四边形的外角等于
它的___________.
定理:如果一个四边形的对角互补,
那么这个四边形的四个顶点_____.
推论:如果四边形的一个外角等于它的
内角的对角,那么这个四边形的四个
顶点共圆.互补内角的对角共圆3.圆的切线的性质与判定及弦切角定理
(1)圆的切线的性质与判定.
性质定理:圆的切线垂直于经过切点的_____.
推论1:经过圆心且垂直于切线的直线必经过_____.
推论2:经过切点且垂直于切线的直线必经过_____.
判定定理:经过半径的外端并且_____于这条半径的直线是圆
的切线.
(2)弦切角定理.
弦切角等于它所夹的弧所对的_______.半径切点圆心垂直圆周角4.与圆有关的比例线段相等相等切线长切线长两条切线判断下面结论是否正确(请在括号中打“√”或“×”).
(1)圆心角等于圆周角的2倍.( )
(2)相等的圆周角所对的弧也相等.( )
(3)任意一个四边形、三角形都有外接圆.( )
(4)等腰梯形一定有外接圆.( )
(5)弦切角所夹弧的度数等于弦切角的度数.( )【解析】(1)错误,若弧不一样,则圆心角与圆周角的关系不确定.
(2)错误,只有同圆或等圆中,相等的圆周角所对的弧才相等.
(3)错误,任意一个四边形不一定有外接圆,但任意一个三角形一定有外接圆.
(4)正确, 可以推出等腰梯形的对角互补,所以有外接圆.(5)错误,弦切角等于它所夹的弧所对的圆周角,所夹的弧的度数等于该弧所对圆心角的度数,所以弦切角所夹弧的度数等于弦切角度数的2倍.
答案:(1)× (2)× (3)× (4)√ (5)×考向 1 圆周角定理
【典例1】(1)(2013·中山模拟)如图,AB为⊙O的直径,弦
AC,BD交于点P,若AB=3,CD=1,则sin∠CBD=____.
(2)(2013·汕头模拟)点A,B,C是圆O上的点,且AB=2,BC=
∠CAB= 则∠ABC=____.【思路点拨】(1)连接AD,结合圆周角定理、正弦定理得到
再利用AD=ABsin∠ABD求解.
(2)连接CO,把∠CAB= 转化为∠BOC= 利用等腰三角形
BOC求出半径,可得△AOB为等腰直角三角形,再利用圆周角定
理转化即可.【规范解答】(1)连接AD,
因为AB是圆O的直径,
所以∠ADB=∠ACB=90°.
又∠ACD=∠ABD,
∠CBD=∠CAD,所以在△ACD中,
由正弦定理得:
= =AB=3,又CD=1,
所以sin∠CAD= 又∠CBD=∠CAD,
所以sin∠CBD=
答案:(2)连接CO,因为∠CAB= 所
以优弧BC所对的圆心角为
从而∠BOC= 在等腰三角形
BOC中可求得半径OB= 因为AB
=2,所以△AOB为等腰直角三角
形,所以∠AOB= 所以
∠AOC= ,∠ABC= ∠AOC= .
答案:【拓展提升】圆周角定理常用的三种转化
(1)圆周角与圆周角之间的转化.
(2)圆周角与圆心角之间的转化.
(3)弧的度数与圆心角和圆周角之间的转化.【变式训练】(1)如图所示,圆的内接三角形ABC的角平分线BD与AC交于点D,与圆交于点E,连接AE,已知ED=3,BD=6,则线段AE的长=____.【解析】∵∠E=∠E,BE平分∠ABC,∠EAD=∠EBC,所以
∠EAD=∠EBA,∴△EDA∽△EAB,
∴ 即AE2=ED·BE=3×9=27,
∴AE=
答案:(2)如图,已知PA,PB是圆O的切线,A,B分别为切点,C为圆O上不与A,B重合的另一点,若∠ACB = 120°,则∠APB =____.【解析】如图所示,连接OA,OB, ∵∠ACB =120°.
∴优弧AB所对的圆心角为240°,从而∠AOB=120°.
又PA,PB是圆O的切线,
∴∠OAP=∠OBP=90°,∴∠APB=60°.
答案:60°考向 2 圆内接四边形的判定与性质
【典例2】(1)如图所示,在梯形ABCD中,AD∥BC,点E,F分别
在边AB,CD上,设ED与AF相交于点G,若B,C,F,E四点共
圆.且AG=1,GF=2,DG= 则GE=____.(2)如图所示,已知AP是⊙O的切线,P为切点,AC是⊙O的割线,与⊙O交于B,C两点,圆心O在∠PAC的内部,点M是BC的中点.若∠OAM=25°,则∠APM =____.【思路点拨】(1)连接EF,由AD∥BC及B,C,F,E四点共圆,可判断A,D,F,E四点共圆,再利用相交弦定理求GE.(2)连接OP,OM,可证 A,P,O,M四点共圆,由∠OAM=∠OPM即可求解.【规范解答】(1)如图所示,
连接EF.
∵B,C,F,E四点共圆,
∴∠ABC=∠EFD.
∵AD∥BC,
∴∠BAD+∠ABC=180°.
∴∠BAD+∠EFD=180°.∴A,D,F,E四点共圆.
由相交弦定理,
可得AG·GF=DG·GE.
因此
答案:(2)连接OP,OM.
∵AP与⊙O相切于点P,
∴OP⊥AP.
∵M是⊙O的弦BC的中点,
∴OM⊥BC,
∴∠OPA+∠OMA=180°,∴A,P,O,M四点共圆.
∴∠OAM=∠OPM =25°,
∴∠APM=90°-25°=65°.
答案:65°【拓展提升】圆内接四边形的重要结论
(1)内接于圆的平行四边形是矩形.
(2)内接于圆的菱形是正方形.
(3)内接于圆的梯形是等腰梯形.【变式训练】(2013·广州模拟)如图,⊙O中,直径AB和弦DE互相垂直,C是DE延长线上一点,连接BC与圆O交于F,若∠CFE=40°,则∠DEB=____.【解析】∵AB⊥DE,∴∠BDE=∠DEB,根据圆的内接四边形性质定理,∠BDE=∠CFE,∴∠DEB=∠CFE=40°.
答案:40°考向 3 圆的切线的性质与判定、弦切角定理
【典例3】(1)(2012·广东高考)如图,圆O的半径为1,A,B,C是圆周上的三点,满足∠ABC=30°,过点A作圆O的切线与OC的延长线交于点P,则PA=____.
(2)如图所示,AB是⊙O的直径,⊙O过BC的中点D,DE⊥AC.若∠ADE=50°,则∠ABD=____.【思路点拨】(1)连接OA,AC从而可得△AOC为等边三角形,∠PAC=30°,△PAC为等腰三角形,再由AC=CP=1可得结果.
(2)连接OD,证明DE是圆O的切线,再利用弦切角定理进行转化即可.【规范解答】(1)连接AO,AC,因为
∠ABC=30°,
∴∠CAP=30°,
∠AOC=60°.
又∵OA=OC,
∴△AOC为等边三角形,则∠ACP=120°,
∴∠APC=30°,∴△ACP为等腰三角形,
且AC=CP=1,∴AP=2×1×sin 60°=
答案:(2)连接OD.∵BD=CD,OA=OB,
∴OD是△ABC的中位线,
∴OD∥AC.
又∵∠DEC=90°,
∴∠ODE=90°.
又∵D在圆周上,
∴DE是⊙O的切线.
因此∠ABD=∠ADE=50°.
答案:50°【互动探究】若例(2)条件不变,则∠BAC=____.
【解析】∵OD⊥DE,∠ADE=50°,∴∠ADO=40°.
∵OD=OA,∴∠DAO=∠ADO=40°.∵OD∥AE,
∴∠DAE=∠ADO=40°,∴∠BAC=∠DAE+∠DAO=40°+40°=80°.
答案:80°【拓展提升】证明直线是圆的切线的常用方法
(1)若已知直线与圆有公共点,则需证明圆心与公共点的连线垂直于已知直线即可.
(2)若已知直线与圆没有明确的公共点,则需证明圆心到直线的距离等于圆的半径.
【提醒】在求解有关角与长度的问题时,注意运用初中阶段所学的知识,如平行线的判定与性质、中垂线的性质、等腰三角形的三线合一、直角三角形的性质等,只有这样才能更灵活地解决问题.【变式备选】(1)如图所示,AB为⊙O的直径,C为⊙O上一点,AD和过C点的切线互相垂直,垂足为D.若∠BAC=35°,则∠CAD=____.【解析】连接OC.
∵CD是⊙O的切线,∴OC⊥CD.
又∵AD⊥CD,∴OC∥AD.由此得∠ACO=∠CAD.
∵OC=OA,∴∠BAC=∠ACO.
∴∠CAD=∠BAC.又∠BAC=35°,
故∠CAD=35°.
答案:35°(2)(2013·湛江模拟)如图,已知PA是圆O的切线,切点为A,直线PO交圆O于B,C两点,AC=2,∠PAB=120°,则圆O的面积为____. 【解析】由题意知∠BAC=90°,则∠PAC=120°-90°=30°.
由弦切角定理知,∠B=30°,∴BC=2AC=4,∴圆O的面积
S=4π.
答案:4π考向 4 与圆有关的比例线段
【典例4】(1)(2012·天津高考)如图,已知AB和AC是圆的两条
弦,过点B作圆的切线与AC的延长线相交于点D,过点C作BD的
平行线与圆相交于点E,与AB相交于点F,AF=3,FB=1,EF=
则线段CD的长为____.(2)如图,△ABC是⊙O的内接三角形,PA是⊙O的切线,PB交AC于点E,交⊙O于点D.若PA=PE,∠ABC=60°,PD=1,PB=9,则PA=____,EC=_____.【思路点拨】(1)利用相交弦定理求CF,再利用切割线定理和比例线段有关知识列方程求解.
(2)利用切割线定理求PA的长度,再判断△PAE为等边三角形,最后用相交弦定理求EC.【规范解答】(1)因为AF·FB=CF·FE,所以CF=2,
又∵ ∴BD=
∵CF∥BD,∴
设CD=x,则AD=4x,∴BD2=x·4x,∴x= .
答案:(2)由切割线定理可知PA2=PD·PB=1×9,
∴PA=3.∵∠ABC=∠PAC=60°,PA=PE,
∴△APE为等边三角形,
∴AE=AP=3,∵PD=1,
∴ED=PE-PD=2,BE=PB-PE=6,
由相交弦定理可知:
AE·EC=BE·ED,∴3·EC=6×2,∴EC=4.
答案:3 4【互动探究】在本例(1)中,若把条件“EF= ”改为“EF=2”,则AD=____.
【解析】设CD=x,则AD=4x,由相交弦定理可得,
AF·FB=EF·CF,所以CF= ,
又∵ ∴BD=2,
又BD2=CD·AD,
所以4=4x2,x=1,所以AD=4.
答案:4【拓展提升】与圆有关的比例线段解题思路
见到圆的两条相交弦就要想到相交弦定理;见到圆的两条割线就要想到割线定理;见到圆的切线和割线就要想到切割线定理.
【提醒】与圆有关的比例线段问题,常常结合方程思想进行计算,即利用代数方法解决几何问题.【变式备选】如图所示,已知P是⊙O外一点,PD为⊙O的切
线,D为切点,割线PEF经过圆心O,若PF=12,PD= 则
∠EFD的度数为____.【解析】由切割线定理得PD2=PE·PF?PE=
=4?EF=8,OD=4.
∵OD⊥PD,OD= PO,∴∠P=30°.
∴∠POD=60°,∠EFD=30°.
答案:30°1.如图所示,AB,AC是⊙O的两条切线,切点分别为B,C,D是优弧BC上的点,已知∠BAC=80°, 那么∠BDC=____.【解析】连接OB,OC,则OB⊥AB,OC⊥AC,
∴∠BOC=180°-∠BAC=100°,
∴∠BDC= ∠BOC=50°.
答案:50°2.(2013·广州模拟)如图所示,过点D作圆的切线切于B点,作割线交圆于A,C两点,其中BD=3,AD=4,AB=2,则BC=___.【解析】由切割线定理得:BD2=CD·AD,∴CD=
又∵∠A=∠DBC,∠D=∠D,∴△ABD∽△BCD,
∴ 解得BC=
答案:3.如图所示,AB,CD是半径为a的圆O的两条弦,它们相交于AB的中点P,PD= ∠OAP=30°,则CP=____.【解析】由题意知OP⊥AB,且AP=BP=
根据相交弦定理得AP2=CP·PD,∴CP= .
答案:4.(2012·湖北高考)如图,点D在⊙O的弦AB上移动,AB=4,连接OD,过点D作OD的垂线交⊙O于点C,则CD的最大值为____.【解析】取AB的中点为E,连接OC,OE,则
= 要求CD的最大值,则点D与E重合.可知结果
为2.
答案:25.如图所示,AC为⊙O的直径,弦BD⊥AC于点P,PC=2,PA=8,则cos∠ACB的值为____.【解析】∵AC是直径,
∴∠ABC=90° ,
又BD⊥AC,
BC2=PC·AC=2×10,
∴BC=
在Rt△BPC中,cos∠ACB=
答案:6. (2013·汕头模拟)如图所示,正△ABC的边长为2,点M,N分别是边AB,AC的中点,直线MN与△ABC的外接圆的交点为P,Q,则线段PM=____.【解析】设PM=x,则QN=x,由相交弦定理可得PM·MQ=
BM·MA,
即x·(x+1)=1,解得
答案:7.如图所示,BD为⊙O的直径,AB=AC,AD交BC于E,AE=2,ED=4.则AB的长为____.【解析】∵AB=AC,∴∠ABC=∠C,
又∵∠C=∠D,∴∠ABC=∠D,又∠BAE=∠DAB,
∴△ABE∽△ADB,
∴AB2=AE·AD,∴AB=
答案:8.(2012·陕西高考)如图所示,在圆O中,直径AB与弦CD垂直,垂足为E,EF⊥DB,垂足为F ,若AB=6,AE=1,则DF·DB=____.【解析】连接AD,因为AB=6,AE=1,所以BE=5, 在Rt△ABD中,DE2=AE·BE=1×5=5,在Rt△BDE中,由射影定理得DF·DB=DE2=5.
答案:59.如图所示,AD是⊙O的切线,AC是⊙O的弦,过C作AD的垂线,垂足为B,CB与⊙O相交于点E,AE平分∠CAB,且AE=2,则AB=_____,AC=_____. 【解析】∵∠CAE=∠EAB,∠EAB=∠ACB,
∴∠ACB=∠CAE=∠EAB.又∵CB⊥AD,
∴∠ACB=∠CAE=∠EAB=30°.
又∵AE=2,∴AB= AC=
答案:10.如图所示,已知圆上的 过C点的圆的切线与BA的延长线交于E点,若∠ACE=35°,则∠BCD=____.【解析】因为 所以∠ABC=∠BCD.又因为EC与圆相切于点C,
故∠ACE=∠ABC.所以∠ACE=∠BCD.
又∠ACE=35°,因此∠BCD=35°.
答案:35°11.如图所示,四边形ABCD是圆O的内接四边形,延长AB和DC相
交于点P,若 则 的值为_____.【解析】由割线定理知:PB·PA=PC·PD,
又∵PA=2PB,PD=3PC,
∴PB·2PB= PD·PD,
∴PB2= PD2,∴PB= PD.
又∵△PBC∽△PDA,
∴
答案:12.如图所示,在△ABC中,AD是高,△ABC的外接圆直径AE交BC边于点G,有下列结论:
①AD2=BD·CD;②BE2=EG·AE;③AE·AD=AB·AC;
④AG·EG=BG·CG.其中正确的结论有____.【解析】①中仅当∠BAC为直角时才成立;②中仅当BG⊥AE时
才成立;因为∠AEB=∠ACD,∠ABE=∠ADC,所以
△AEB∽△ACD,故 即AE·AD=AB·AC,故③正确;
由相交弦定理知④正确.
答案:③④13.(2012·广东高考)如图所示,直线PB与圆O相切于点B,D是弦AC上的点,∠PBA=∠DBA.若AD=m,AC=n,则AB=____.【解析】由题意知∠ABP=∠ACB=∠ABD,
又∠A=∠A,所以△ABD∽△ACB,
所以
所以AB= =
答案:14.如图所示,四边形ABCD内接于⊙O,BC是直径,MN与⊙O相切,切点为A,∠MAB=35°,则∠ADC=____.【解析】连接BD,
由题意知,∠ADB=∠MAB=35°,∠BDC=90°,故∠ADC=∠ADB+∠BDC=125°.
答案:125°15.EB,EC是⊙O的两条切线,B,C是切点,A,D是⊙O上的两点,如果∠E=46°,∠DCF=32°,那么∠BAD=_____.【解析】连接OB,OC,AC,
根据弦切角定理,可得∠BAD=∠BAC+∠CAD=
(180°-∠E)+∠DCF=67°+32°=99°.
答案:99°16.如图所示,AB是⊙O的直径,CB切⊙O于点B,CD切⊙O于点D,直线CD交直线AB于点E.若AB=3,ED=2,则CB的长为___.【解析】由切割线定理得,ED2=EA·EB,
∴4=EA(EA+3),
∴EA=1.∵CB是⊙O的切线,∴EB⊥CB,
∴EB2+CB2=CE2.
又∵CD是⊙O的切线,∴CD=CB,
∴42+CB2=(CB+2)2,∴CB=3.
答案:317.如图所示,AB为⊙O的直径,C为⊙O上一点,AP和过C的切线互相垂直,垂足为P,过B的切线交过C的切线于T,PB交⊙O于Q,若∠BTC=120°,AB=4,则PQ·PB=____.【解析】连接OC,AC,则OC⊥PC,则O,C,T,B四点共圆,
∵∠BTC=120°,∴∠COB=60°,
故∠AOC=120°.
由AO=OC=2,知AC=
在Rt△APC中,∠ACP=60°,
因此PC=
根据切割线定理得PQ·PB=PC2=3.
答案:318.(2013·佛山模拟)如图所示,AB是⊙O的直径,D为⊙O上一点,过D作⊙O的切线交AB的延长线于点C,若DA=DC,且BC=5,则AB=____.【解析】如图所示,连接OD,∵CD是⊙O的切线,
∴∠ODC=90°.
设∠C=θ,则∠A=θ,∠ADO=θ.∵θ+θ+θ+90°=180°,∴θ=30°,
∴OC=2OD.
设圆O的半径为r,则OC=2r,∴BC=r.
∴AB=2BC=10.
答案:1019.如图所示,已知⊙O的直径AB=5,C为圆周上一点,BC=4,过点C作⊙O的切线l,过点A作l的垂线AD,垂足为D,则CD=____.【解析】∵CD是⊙O的切线,
∴∠B=∠ACD,
又AB为直径,∴∠ACB=∠ADC=90°,
∴△ABC∽△ACD,∴
∵AB=5,BC=4,∴AC=3,∴CD=
答案:20.如图所示,割线PBC经过圆心O,OB=PB=1,OB绕点O逆时针旋转120°到OD,连接PD交圆O于点E,则PE=____.【解析】依题意得,
PD=
又PE·PD=PB·PC,
因此PE=
答案:21.Rt△ABC中,∠C=90°,∠A=30°,圆O经过B,C且与
AB,AC相交于D,E.若AE=EC= 则AD=___,圆O的半径
r=____.【解析】在Rt△ABC中,∠BAC=30°,AC= 所以BC=4,
AB=8,由割线定理得AE·AC=AD·AB,所以AD=
因为∠C=90°,连接BE,则BE是圆O的直
径.所以 所以圆O的半径r= .
答案:3 22.如图所示,A,E是半圆周上的两个三等分点,直径BC=4,AD⊥BC,垂足为D,BE与AD相交于点F,则AF的长为_____.【解析】如图,连接CE,AO,AB.根据A,E是半圆周上的两个三等分点,BC为直径,可得∠CEB=90°,∠CBE=30°,∠AOB=60°,故△AOB为等边三角形,AD=
OD=BD=1,∴DF=
∴AF=AD-DF=
答案:23.已知EB是半圆O的直径,A是BE延长线上一点,AC切半圆O于点D,BC⊥AC于点C,若BC=6,AC=8,则AE=____,
AD=____.【解析】∵OD⊥AC,BC⊥AC,
∴△ADO∽△ACB,∴
∵BC=6,AC=8,∴AB=10,
设OD=R,则AO= R,∴R+ R=10,∴R=
AE=AB-2R= , ∴AD=5.
答案: 524.如图所示,过圆C外一点P作一条直线与圆C交于A,B两点,AB=2AP,PT与圆C相切于T点.已知圆C的半径为2,∠CAB=30°,则PT=_____.【解析】∵AC=2,∠CAB=30°,
∴AB=2ACcos 30°=2×2× =
∴AP= AB= ∴PB=AP+AB=
∵PT是⊙C的切线,∴PT2=AP·PB=9,
∴PT=3.
答案:325.如图所示,已知⊙O1与⊙O2相交于A,B两点,过点B作两圆的割线,分别交⊙O1,⊙O2于点D,E.过E作CE∥AD交⊙O2于C,连AC交DE于点P. 若AD是⊙O2的切线,且PA=6,PC=2,BD=9,则AD的长为_____.【解析】设BP=x,PE=y.
∵PA=6,PC=2,
∴由相交弦定理得PA·PC=BP·PE,即xy=12①,
∵AD∥CE,∴ ∴ ②,
由①②可得,∴DE=9+x+y=16.
∵AD是⊙O2的切线,DE是⊙O2的割线,
∴AD2=BD·DE=9×16,∴AD=12.
答案:12
