【全程复习方略】2014-2015学年高中数学理(人教广东版)教师配套课件选修4-1第一节相似三角形的判定及有关性质(共80张PPT)
文档属性
| 名称 | 【全程复习方略】2014-2015学年高中数学理(人教广东版)教师配套课件选修4-1第一节相似三角形的判定及有关性质(共80张PPT) |

|
|
| 格式 | zip | ||
| 文件大小 | 2.3MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教新课标A版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2014-12-26 00:00:00 | ||
图片预览










文档简介
课件80张PPT。选修4-1 几何证明选讲
第一节 相似三角形的判定及有关性质1.平行线等分线段定理相等平分平分2.平行线分线段成比例定理
(1)定理:三条平行线截两条直线,所得的_________成比例.
(2)推论:平行于三角形一边的直线截其他两边(或两边的延长
线)所得的对应线段_______.
3.相似三角形的判定及性质
(1)相似三角形的判定.
①定义:对应角_____,对应边_______的两个三角形叫做相似
三角形.对应线段成比例相等成比例②预备定理:平行于三角形一边的直线和其他两边(或两边的
延长线)_____,所构成的三角形与原三角形_____.
③判定:
定理1:两角对应_____,两三角形相似.
定理2:两边对应_______且夹角_____,两三角形相似.
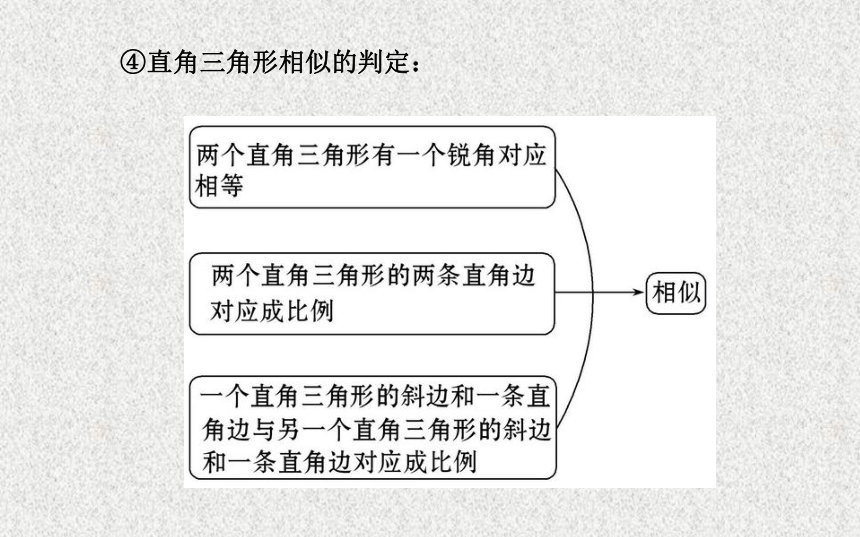
定理3:三边对应_______,两三角形相似.相交相似相等成比例相等成比例④直角三角形相似的判定:(2)相似三角形的性质.
①相似三角形对应高的比、对应中线的比和对应角平分线的比
都等于_______.
②相似三角形周长的比等于_______.
③相似三角形面积的比等于相似比的_____.
④相似三角形外接圆的直径比、周长比等于_______,外接圆的
面积比等于相似比的_____.相似比相似比平方相似比平方4.直角三角形的射影定理
定理:直角三角形斜边上的高是_____________________的比例
中项;两直角边分别是它们在斜边上射影与斜边的_________.两直角边在斜边上射影比例中项判断下面结论是否正确(请在括号中打“√”或“×”).
(1)三角形相似不具有传递性.( )
(2)相似多边形不具有面积比等于相似比的平方的性质.( )
(3)相似三角形的内切圆的半径之比等于相似比.( )
(4)两组对应边成比例,一组对应边所对的角相等的两三角形相似.( )【解析】(1)错误,三角形相似具有传递性,即△ABC∽△A1B1C1,△A1B1C1∽△A2B2C2,则△ABC∽△A2B2C2.
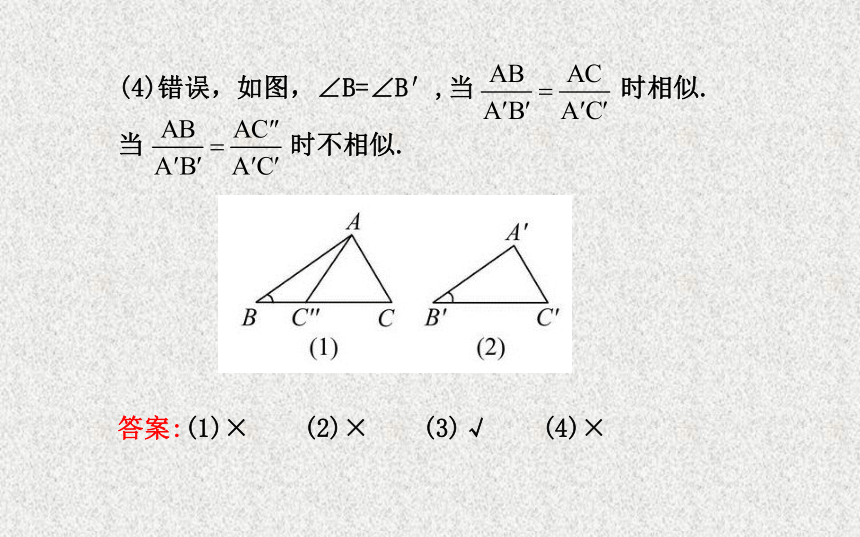
(2)错误,可以通过作辅助线将多边形转化为三角形加以证明.(3)正确,由相似三角形的定义知,∠BAC=∠B′A′C′,∠1=∠2,由直角三角形相似的判定方法知,Rt△ADI∽Rt△A′D′I′,可知结论正确.(4)错误,如图,∠B=∠B′,当 时相似.
当 时不相似.
答案:(1)× (2)× (3)√ (4)×考向 1 平行线分线段成比例定理
【典例1】(1)(2013·西安模拟)如图所示,已知DE∥BC,
BF∶EF=3∶2,则AC∶AE=____,AD∶DB=____.
(2)如图所示,F为?ABCD边AB上一点,连接DF交AC于G,并延长
DF交CB的延长线于E,若DE=5,DF=4,则 =____.【思路点拨】(1)利用平行线分线段成比例定理的推论,列比例式求解.
(2)利用平行线分线段成比例定理及推论,经中间比值代换求值.【规范解答】(1)∵DE∥BC,∴
∵BF∶EF=3∶2,∴
∴AC∶AE=3∶2.
同理DE∥BC,得AB∶AD=3∶2,即
∴ 即
即AD∶BD=2∶1.
答案:3∶2 2∶1(2)∵四边形ABCD是平行四边形,
∴AD∥BC,AB∥DC,AD=BC.
∵AD∥BC,∴
又∵AB∥DC,∴
∴
答案:【互动探究】本例(2)中条件不变,结论改为 =____.
【解析】∵AD∥BC,
∴
答案:【拓展提升】平行线分线段成比例定理及其推论的应用
(1)平行线等分线段定理及其推论是证明两条线段相等的重要依据,特别是在应用推论时,一定要明确哪一条线段平行于三角形的一边,是否过一边的中点.
(2)利用平行线分线段成比例定理解决问题时要特别注意被平行线所截的直线,找准成比例的线段,得到相应的比例式,有时需要进行适当的变形,从而得到最终的结果.【变式备选】(2013·广州模拟)在梯形ABCD中,AD∥BC,AD=
2,BC=5,点E,F分别在AB,CD上,且EF∥AD,若 则EF
的长为____.【解析】如图所示,延长BA,CD交于点P,
∵AD∥BC,∴
∴ 又∵
∴ ∴
∴ ∵AD∥EF,∴
又AD=2,∴EF=
答案:考向 2 相似三角形的判定与性质
【典例2】(1)如图所示,△ABC中,∠BAC=90°,AD⊥BC交
BC于点D,若E是AC的中点,ED的延长线交AB的延长线于F,若
则 =____.
(2)如图所示,平行四边形ABCD的对角线交于点O,OE交BC于E,
交AB的延长线于F,若AB=a,BC=b,BF=c,则BE=____.【思路点拨】(1)通过∠BDF=∠EDC=∠BAD,证明△DBF∽△ADF,再根据相似三角形的对应边成比例可得结果.
(2)过O作OG∥BC,交AB于G,构造△BEF∽△GOF求解.【规范解答】(1)∵E为Rt△ADC斜边AC的中点,
∴DE=EC,则∠C=∠EDC.
又AD⊥BC,且∠BAC=90°,
∴∠BAD=∠C,
从而∠BDF=∠EDC=∠BAD.
又∠F=∠F,
因此△DBF∽△ADF,
∴
答案:(2)过O作OG∥BC,交AB于G,显然GO是△ABC的中位线,所以
GO= BC= b,
GB= AB= a.在△GOF中,BE∥OG,
所以△BEF∽△GOF,所以
即
答案:【拓展提升】相似三角形证明方法
证明三角形相似时一般的思考程序是:
(1)先找两对内角对应相等.
(2)若只有一个角对应相等,再判定这个角的两邻边是否对应成比例.
(3)若无角对应相等,就要证明三边对应成比例.
【提醒】在解决相似三角形时,一定要注意对应角和对应边,否则容易出错.【变式训练】(1)(2013·汕头模拟)如图所示的Rt△ABC中有边
长分别为a,b,c的三个正方形,若ac=4,则b=____.
【解析】由三角形相似知
∴ac-bc=b2-bc,∴b2=ac.∴b= =2.
答案:2(2)如图,在△ABC中,M,N分别是AB,BC的中点,AN,CM交于
点O,那么△MON与△AOC面积的比是____.
【解析】∵M,N分别是AB,BC的中点,故MN∥AC,MN= AC,
∴△MON∽△COA,∴
答案:1∶4 考向 3 射影定理及其应用
【典例3】(1)如图所示,在△ABC中,AD⊥BC于D,DE⊥AB于E,DF⊥AC于F.若AE·AB=5,则AF·AC=____.
(2)在直角三角形ABC中,AB=4,AC=3,过点A作AD⊥BC,垂足为D,过点D作DE⊥AC,垂足为E,则DE=____.【思路点拨】(1)由垂直条件,联想射影定理,然后进行计算.
(2)首先利用勾股定理求BC,再结合射影定理和三角形面积公式即可求解.【规范解答】(1)∵AD⊥BC,
∴△ADB为直角三角形,
又∵DE⊥AB,由射影定理知,AD2=AE·AB.
在Rt△ADC中,同理可得AD2=AF·AC,
又AE·AB=5,∴AF·AC=AE·AB=5.
答案:5(2)由勾股定理得:BC= =5,
由射影定理得:CD=
由三角形面积得:AD=
由三角形面积得:DE=
答案:【拓展提升】直角三角形中成比例线段问题的解决方法
(1)如图,Rt△ABC中,若CD为高,则有CD2=BD·AD,BC2=BD·AB,AC2=AD·AB,利用上面等
积式和勾股定理,已知图中的任意两
条线段,可求出其余四条线段.
(2)直角三角形中出现斜边上的高这一
条件时,射影定理是经常使用的结论,注意灵活运用.【变式训练】在△ABC中,∠ACB=90°,CD⊥AB,AE平分∠BAC交BC于E,CE∶EB=4∶5,CD=24,则AD∶DB=____.【解析】∵∠ACB=90°,CD⊥AB,
∴AC2=AD·AB,BC2=BD·AB,∴
而AC2+BC2=AB2,
∴
又AE平分∠BAC,∴
∴
答案:16∶9 1.如图,∠1=∠B,AD=5,AB=10,则AC的长度为____.【解析】因为∠1=∠B,∠A=∠A,
所以△ACD∽△ABC,所以
AC2=AD·AB=50,即AC=
答案:2.如图所示,D,E分别是△ABC的边AB,
AC上的点,DE∥BC,且AD∶DB=2,那么
△ADE与四边形DBCE的面积比是____.
【解析】∵ =2,∴
故 ∴
答案:3.如图,已知在△ABC中,∠ACB=90°,CD⊥AB于D,AC=6,DB=5,则AD的长为_____.【解析】在Rt△ABC中,∠ACB=90°,CD⊥AB,
∴AC2=AD·AB.
设AD=x,则AB=x+5,又AC=6,
∴62=x(x+5),即x2+5x-36=0,
解得x=4或x=-9(舍去),
∴AD=4.
答案:44.(2013·茂名模拟)△ABC中,AC=6,BC=4,BA=9,
△ABC∽△A′B′C′,且△A′B′C′的最短边的长度为12,
则它的最长边的长度为____.
【解析】由△ABC∽△A′B′C′及AC=6,BC=4,BA=9可
知,△A′B′C′的最短边为B′C′,最长边为B′A′.又
即 解得B′A′=27.
答案:275.如图,∠CAB=∠BCD,AD=2,BD=4,
则BC=____.
【解析】∵∠CAB=∠BCD,
∠B=∠B,∴△CAB∽△DCB,
∴
∴BC2=BD·AB=4×(2+4)=24,
∴BC=
答案:6.如图,已知在梯形ABCD中,上底长为2,下底长为6,高为4,对角线AC和BD相交于点P.
(1)若AP的长为4,则PC
=____.
(2)△ABP和△CDP高的比为____.【解析】(1)∵AB∥CD,∴△ABP∽△CDP,
∴
即 解得PC=12.
(2)由△ABP∽△CDP及△ABP和△CDP的高的比等于它们的相似
比,得这两个三角形的高的比为1∶3.
答案:(1)12 (2)1∶37.如图,在△ABC中,D是AC的中点,E是BD的中点,延长AE交BC于F,
则 =____.【解析】如图,过D作DG∥BC交AF于G,∵E是BD的中点,∴DG=BF.
又∵DG∥BC,
∴
∴
答案:8.如图,在矩形ABCD中,BD为对角线,AE⊥BD,AB= AD=1,则BE=____.【解析】∵矩形各内角为直角,∴△ABD为直角三角形.
在直角△ABD中,AB= AD=1,
则
再由射影定理,得AB2=BE·BD,
∴
答案:9.一个直角三角形两条直角边的比为1∶ 则它们在斜边上
的射影比为____.【解析】如图,在Rt△ABC中,
BC∶AC=1∶ CD⊥AB于D.
∴BC2=BD·AB,AC2
=AD·AB,
∴ ∴
因此它们在斜边上的射影比为1∶5.
答案:1∶510.如图所示,在梯形ABCD中,AB∥CD,AB=4,CD=2,E,F分别为AD,BC上的点,且EF=3,EF∥AB,则梯形EFCD与梯形ABFE的面积比为____.【解析】由题得EF是梯形的中位线,
设梯形ABCD的高为2h,
∴
答案:11.(2013·惠州模拟)如图,在△ABC中,DE∥BC,DF∥AC,AE∶AC=3∶5,DE=6,则BF=____.【解析】因为DE∥BC,所以△ADE∽△ABC,所以 即 所以BC=10.又DF∥AC,所以四边形DECF是平行四边形,故BF=BC-FC=BC-DE=10-6=4.
答案:412.如图所示,∠B=∠D,AE⊥BC,∠ACD=90°,且AB=6,AC=4,AD=12,则AE=____.
【解析】Rt△ABE∽Rt△ADC,所以 即AE=
答案:213.如图所示,F为 的边AD延长线上的一点,DF=
AD,BF分别交DC,AC于点G,E,EF=16,GF=12,则BE的长
为____.【解析】∵DC∥AB,AD=DF,∴BG=GF=12,
又EF=16,GF=12,∴GE=16-12=4,
∴BE=BG-GE=12-4=8.
答案:814.如图,已知D为△ABC中AC边的中点,AE∥BC,ED交AB于G,
交BC延长线于F,若BG∶GA=3∶1,BC=8,则AE=____.【解析】∵AE∥BC,D为AC的中点,
∴AE=CF,
设AE=x,
又BC=8,∴
∴x=4,∴AE=4.
答案:415.如图所示,已知在△ABC中,∠C=90°,正方形DEFC
内接于△ABC,DE∥AC,EF∥BC,AC=1,BC=2,则AF∶FC
等于____.【解析】设正方形边长为x,则由△AFE∽△ACB,可得
即 所以x= 于是AF∶FC=1∶2.
答案:1∶216.如图所示,在△ABC中,∠ACB=90°,CD⊥AB于D,AD∶BD=2∶3,则△ACD与△CBD的相似比为____.【解析】在Rt△ACB中,CD⊥AB,由射影定理得:
CD2=AD·BD,
又∵AD∶BD=2∶3,令AD=2x,BD=3x(x>0),
∴CD2=6x2,∴CD=
又∵∠ADC=∠BDC=90°,∴△ACD∽△CBD.
易知△ACD与△CBD的相似比为
即相似比为
答案: ∶317.如图,在梯形ABCD中,AB∥CD,且AB=2CD,E,F分别是AB,BC的中点,EF与BD相交于点M.若DB=9,则BM=____.【解析】∵E是AB的中点,∴AB=2EB.∵AB=2CD,∴CD=EB.
又AB∥CD,∴四边形CBED是平行四边形.∴CB∥DE,
∴△EDM∽△FBM.
∴ ∵F是BC的中点,∴DE=2BF.
∴DM=2BM,∴BM= DB=3.
答案:318.如图,已知AB∥EF∥CD,若AB=6,CD=9,则EF=____.【解析】在△ABC中,因为EF∥AB,所以
在△DBC中,因为EF∥CD,所以
两式相加,得
所以 故EF=
答案:19.如图,梯形ADHE中,AE∥BF∥CG∥DH,AB= BC=CD,AE=12,DH=16,AH交BF于M,则BM=____,CG=____.【解析】∵AE∥BF∥CG∥DH,AB= BC=CD,AE=12,DH=16,∴ ∴ ∴BM=4.
取BC的中点P,作PQ∥DH交EH于Q,如图,则PQ是梯形ADHE的中位线,∴PQ= (AE+DH)= (12+16)=14.同理:CG= (PQ+DH)= (14+16)=15.
答案: 4 1520.如图,已知AD∥EG∥BC,AD=6,BC=9, 则GF的长
为____.【解析】∵AD∥EG∥BC,
∴
∵ ∴ ∴
又∵AD=6,BC=9,∴EF=2,EG=6,
∴GF=EG-EF=4.
答案:421.(2013·三亚模拟)如图所示,身高为1.6米的某学生想测量学校旗杆的高度,当他站在C处时,他的影子的顶端正好与旗杆影子的顶端重合,并测得AC=2米,BC=8米,则旗杆的高度是____米.【解析】由题意,知CD∥BE.∴△ACD∽△ABE,
∴ ∵AC=2米,BC=8米,∴AB=10米.
又∵CD=1.6米,∴ ∴BE=8米.
答案:822.如图,在△ABC中,DE∥BC,
EF∥CD,且AB=2,AD= 则AF=____.
【解析】∵DE∥BC,∴
∵EF∥CD,∴
∴ ∴AD2=AF·AB.
∵AB=2,AD= ∴AF=1.
答案:123.在矩形ABCD中,AE⊥BD于E,矩形的面积为40 cm2, S△ABE∶S△DBA=1∶5,则AE的长为 ____cm.【解析】∵S△ABE∶S△DBA=1∶5,
∴S△ABE∶S矩形ABCD=1∶10,
∴S△ABE= S矩形ABCD= ×40=4(cm2).
由△ABE∽△DAE易证相似比为1∶2,
即BE∶AE=1∶2,
设BE=x cm,则AE=2x cm,
∴ x·2x=4,∴x=2,∴AE=4 cm.
答案:424.如图,在梯形ABCD中,AD∥BC,BD,AC相交于O.过O的直线分别交AB,CD于E,F,且EF∥BC,若AD=12,BC=20,则EF=___.【解析】∵EF∥BC,AD=12,BC=20,
∴
∵OE∥BC,∴ ∴OE=
∵OF∥AD,∴ ∴OF=
∴EF=OE+OF= =15.
答案:1525.如图,ABCD为正方形,A,E,F,G在同一条直线上,且AE=6,EF=4,那么FG=____.【解析】∵DF∥AB,∴
∴
又∵CF∥AB,∴
即 ∴FG=5.
答案:5
第一节 相似三角形的判定及有关性质1.平行线等分线段定理相等平分平分2.平行线分线段成比例定理
(1)定理:三条平行线截两条直线,所得的_________成比例.
(2)推论:平行于三角形一边的直线截其他两边(或两边的延长
线)所得的对应线段_______.
3.相似三角形的判定及性质
(1)相似三角形的判定.
①定义:对应角_____,对应边_______的两个三角形叫做相似
三角形.对应线段成比例相等成比例②预备定理:平行于三角形一边的直线和其他两边(或两边的
延长线)_____,所构成的三角形与原三角形_____.
③判定:
定理1:两角对应_____,两三角形相似.
定理2:两边对应_______且夹角_____,两三角形相似.
定理3:三边对应_______,两三角形相似.相交相似相等成比例相等成比例④直角三角形相似的判定:(2)相似三角形的性质.
①相似三角形对应高的比、对应中线的比和对应角平分线的比
都等于_______.
②相似三角形周长的比等于_______.
③相似三角形面积的比等于相似比的_____.
④相似三角形外接圆的直径比、周长比等于_______,外接圆的
面积比等于相似比的_____.相似比相似比平方相似比平方4.直角三角形的射影定理
定理:直角三角形斜边上的高是_____________________的比例
中项;两直角边分别是它们在斜边上射影与斜边的_________.两直角边在斜边上射影比例中项判断下面结论是否正确(请在括号中打“√”或“×”).
(1)三角形相似不具有传递性.( )
(2)相似多边形不具有面积比等于相似比的平方的性质.( )
(3)相似三角形的内切圆的半径之比等于相似比.( )
(4)两组对应边成比例,一组对应边所对的角相等的两三角形相似.( )【解析】(1)错误,三角形相似具有传递性,即△ABC∽△A1B1C1,△A1B1C1∽△A2B2C2,则△ABC∽△A2B2C2.
(2)错误,可以通过作辅助线将多边形转化为三角形加以证明.(3)正确,由相似三角形的定义知,∠BAC=∠B′A′C′,∠1=∠2,由直角三角形相似的判定方法知,Rt△ADI∽Rt△A′D′I′,可知结论正确.(4)错误,如图,∠B=∠B′,当 时相似.
当 时不相似.
答案:(1)× (2)× (3)√ (4)×考向 1 平行线分线段成比例定理
【典例1】(1)(2013·西安模拟)如图所示,已知DE∥BC,
BF∶EF=3∶2,则AC∶AE=____,AD∶DB=____.
(2)如图所示,F为?ABCD边AB上一点,连接DF交AC于G,并延长
DF交CB的延长线于E,若DE=5,DF=4,则 =____.【思路点拨】(1)利用平行线分线段成比例定理的推论,列比例式求解.
(2)利用平行线分线段成比例定理及推论,经中间比值代换求值.【规范解答】(1)∵DE∥BC,∴
∵BF∶EF=3∶2,∴
∴AC∶AE=3∶2.
同理DE∥BC,得AB∶AD=3∶2,即
∴ 即
即AD∶BD=2∶1.
答案:3∶2 2∶1(2)∵四边形ABCD是平行四边形,
∴AD∥BC,AB∥DC,AD=BC.
∵AD∥BC,∴
又∵AB∥DC,∴
∴
答案:【互动探究】本例(2)中条件不变,结论改为 =____.
【解析】∵AD∥BC,
∴
答案:【拓展提升】平行线分线段成比例定理及其推论的应用
(1)平行线等分线段定理及其推论是证明两条线段相等的重要依据,特别是在应用推论时,一定要明确哪一条线段平行于三角形的一边,是否过一边的中点.
(2)利用平行线分线段成比例定理解决问题时要特别注意被平行线所截的直线,找准成比例的线段,得到相应的比例式,有时需要进行适当的变形,从而得到最终的结果.【变式备选】(2013·广州模拟)在梯形ABCD中,AD∥BC,AD=
2,BC=5,点E,F分别在AB,CD上,且EF∥AD,若 则EF
的长为____.【解析】如图所示,延长BA,CD交于点P,
∵AD∥BC,∴
∴ 又∵
∴ ∴
∴ ∵AD∥EF,∴
又AD=2,∴EF=
答案:考向 2 相似三角形的判定与性质
【典例2】(1)如图所示,△ABC中,∠BAC=90°,AD⊥BC交
BC于点D,若E是AC的中点,ED的延长线交AB的延长线于F,若
则 =____.
(2)如图所示,平行四边形ABCD的对角线交于点O,OE交BC于E,
交AB的延长线于F,若AB=a,BC=b,BF=c,则BE=____.【思路点拨】(1)通过∠BDF=∠EDC=∠BAD,证明△DBF∽△ADF,再根据相似三角形的对应边成比例可得结果.
(2)过O作OG∥BC,交AB于G,构造△BEF∽△GOF求解.【规范解答】(1)∵E为Rt△ADC斜边AC的中点,
∴DE=EC,则∠C=∠EDC.
又AD⊥BC,且∠BAC=90°,
∴∠BAD=∠C,
从而∠BDF=∠EDC=∠BAD.
又∠F=∠F,
因此△DBF∽△ADF,
∴
答案:(2)过O作OG∥BC,交AB于G,显然GO是△ABC的中位线,所以
GO= BC= b,
GB= AB= a.在△GOF中,BE∥OG,
所以△BEF∽△GOF,所以
即
答案:【拓展提升】相似三角形证明方法
证明三角形相似时一般的思考程序是:
(1)先找两对内角对应相等.
(2)若只有一个角对应相等,再判定这个角的两邻边是否对应成比例.
(3)若无角对应相等,就要证明三边对应成比例.
【提醒】在解决相似三角形时,一定要注意对应角和对应边,否则容易出错.【变式训练】(1)(2013·汕头模拟)如图所示的Rt△ABC中有边
长分别为a,b,c的三个正方形,若ac=4,则b=____.
【解析】由三角形相似知
∴ac-bc=b2-bc,∴b2=ac.∴b= =2.
答案:2(2)如图,在△ABC中,M,N分别是AB,BC的中点,AN,CM交于
点O,那么△MON与△AOC面积的比是____.
【解析】∵M,N分别是AB,BC的中点,故MN∥AC,MN= AC,
∴△MON∽△COA,∴
答案:1∶4 考向 3 射影定理及其应用
【典例3】(1)如图所示,在△ABC中,AD⊥BC于D,DE⊥AB于E,DF⊥AC于F.若AE·AB=5,则AF·AC=____.
(2)在直角三角形ABC中,AB=4,AC=3,过点A作AD⊥BC,垂足为D,过点D作DE⊥AC,垂足为E,则DE=____.【思路点拨】(1)由垂直条件,联想射影定理,然后进行计算.
(2)首先利用勾股定理求BC,再结合射影定理和三角形面积公式即可求解.【规范解答】(1)∵AD⊥BC,
∴△ADB为直角三角形,
又∵DE⊥AB,由射影定理知,AD2=AE·AB.
在Rt△ADC中,同理可得AD2=AF·AC,
又AE·AB=5,∴AF·AC=AE·AB=5.
答案:5(2)由勾股定理得:BC= =5,
由射影定理得:CD=
由三角形面积得:AD=
由三角形面积得:DE=
答案:【拓展提升】直角三角形中成比例线段问题的解决方法
(1)如图,Rt△ABC中,若CD为高,则有CD2=BD·AD,BC2=BD·AB,AC2=AD·AB,利用上面等
积式和勾股定理,已知图中的任意两
条线段,可求出其余四条线段.
(2)直角三角形中出现斜边上的高这一
条件时,射影定理是经常使用的结论,注意灵活运用.【变式训练】在△ABC中,∠ACB=90°,CD⊥AB,AE平分∠BAC交BC于E,CE∶EB=4∶5,CD=24,则AD∶DB=____.【解析】∵∠ACB=90°,CD⊥AB,
∴AC2=AD·AB,BC2=BD·AB,∴
而AC2+BC2=AB2,
∴
又AE平分∠BAC,∴
∴
答案:16∶9 1.如图,∠1=∠B,AD=5,AB=10,则AC的长度为____.【解析】因为∠1=∠B,∠A=∠A,
所以△ACD∽△ABC,所以
AC2=AD·AB=50,即AC=
答案:2.如图所示,D,E分别是△ABC的边AB,
AC上的点,DE∥BC,且AD∶DB=2,那么
△ADE与四边形DBCE的面积比是____.
【解析】∵ =2,∴
故 ∴
答案:3.如图,已知在△ABC中,∠ACB=90°,CD⊥AB于D,AC=6,DB=5,则AD的长为_____.【解析】在Rt△ABC中,∠ACB=90°,CD⊥AB,
∴AC2=AD·AB.
设AD=x,则AB=x+5,又AC=6,
∴62=x(x+5),即x2+5x-36=0,
解得x=4或x=-9(舍去),
∴AD=4.
答案:44.(2013·茂名模拟)△ABC中,AC=6,BC=4,BA=9,
△ABC∽△A′B′C′,且△A′B′C′的最短边的长度为12,
则它的最长边的长度为____.
【解析】由△ABC∽△A′B′C′及AC=6,BC=4,BA=9可
知,△A′B′C′的最短边为B′C′,最长边为B′A′.又
即 解得B′A′=27.
答案:275.如图,∠CAB=∠BCD,AD=2,BD=4,
则BC=____.
【解析】∵∠CAB=∠BCD,
∠B=∠B,∴△CAB∽△DCB,
∴
∴BC2=BD·AB=4×(2+4)=24,
∴BC=
答案:6.如图,已知在梯形ABCD中,上底长为2,下底长为6,高为4,对角线AC和BD相交于点P.
(1)若AP的长为4,则PC
=____.
(2)△ABP和△CDP高的比为____.【解析】(1)∵AB∥CD,∴△ABP∽△CDP,
∴
即 解得PC=12.
(2)由△ABP∽△CDP及△ABP和△CDP的高的比等于它们的相似
比,得这两个三角形的高的比为1∶3.
答案:(1)12 (2)1∶37.如图,在△ABC中,D是AC的中点,E是BD的中点,延长AE交BC于F,
则 =____.【解析】如图,过D作DG∥BC交AF于G,∵E是BD的中点,∴DG=BF.
又∵DG∥BC,
∴
∴
答案:8.如图,在矩形ABCD中,BD为对角线,AE⊥BD,AB= AD=1,则BE=____.【解析】∵矩形各内角为直角,∴△ABD为直角三角形.
在直角△ABD中,AB= AD=1,
则
再由射影定理,得AB2=BE·BD,
∴
答案:9.一个直角三角形两条直角边的比为1∶ 则它们在斜边上
的射影比为____.【解析】如图,在Rt△ABC中,
BC∶AC=1∶ CD⊥AB于D.
∴BC2=BD·AB,AC2
=AD·AB,
∴ ∴
因此它们在斜边上的射影比为1∶5.
答案:1∶510.如图所示,在梯形ABCD中,AB∥CD,AB=4,CD=2,E,F分别为AD,BC上的点,且EF=3,EF∥AB,则梯形EFCD与梯形ABFE的面积比为____.【解析】由题得EF是梯形的中位线,
设梯形ABCD的高为2h,
∴
答案:11.(2013·惠州模拟)如图,在△ABC中,DE∥BC,DF∥AC,AE∶AC=3∶5,DE=6,则BF=____.【解析】因为DE∥BC,所以△ADE∽△ABC,所以 即 所以BC=10.又DF∥AC,所以四边形DECF是平行四边形,故BF=BC-FC=BC-DE=10-6=4.
答案:412.如图所示,∠B=∠D,AE⊥BC,∠ACD=90°,且AB=6,AC=4,AD=12,则AE=____.
【解析】Rt△ABE∽Rt△ADC,所以 即AE=
答案:213.如图所示,F为 的边AD延长线上的一点,DF=
AD,BF分别交DC,AC于点G,E,EF=16,GF=12,则BE的长
为____.【解析】∵DC∥AB,AD=DF,∴BG=GF=12,
又EF=16,GF=12,∴GE=16-12=4,
∴BE=BG-GE=12-4=8.
答案:814.如图,已知D为△ABC中AC边的中点,AE∥BC,ED交AB于G,
交BC延长线于F,若BG∶GA=3∶1,BC=8,则AE=____.【解析】∵AE∥BC,D为AC的中点,
∴AE=CF,
设AE=x,
又BC=8,∴
∴x=4,∴AE=4.
答案:415.如图所示,已知在△ABC中,∠C=90°,正方形DEFC
内接于△ABC,DE∥AC,EF∥BC,AC=1,BC=2,则AF∶FC
等于____.【解析】设正方形边长为x,则由△AFE∽△ACB,可得
即 所以x= 于是AF∶FC=1∶2.
答案:1∶216.如图所示,在△ABC中,∠ACB=90°,CD⊥AB于D,AD∶BD=2∶3,则△ACD与△CBD的相似比为____.【解析】在Rt△ACB中,CD⊥AB,由射影定理得:
CD2=AD·BD,
又∵AD∶BD=2∶3,令AD=2x,BD=3x(x>0),
∴CD2=6x2,∴CD=
又∵∠ADC=∠BDC=90°,∴△ACD∽△CBD.
易知△ACD与△CBD的相似比为
即相似比为
答案: ∶317.如图,在梯形ABCD中,AB∥CD,且AB=2CD,E,F分别是AB,BC的中点,EF与BD相交于点M.若DB=9,则BM=____.【解析】∵E是AB的中点,∴AB=2EB.∵AB=2CD,∴CD=EB.
又AB∥CD,∴四边形CBED是平行四边形.∴CB∥DE,
∴△EDM∽△FBM.
∴ ∵F是BC的中点,∴DE=2BF.
∴DM=2BM,∴BM= DB=3.
答案:318.如图,已知AB∥EF∥CD,若AB=6,CD=9,则EF=____.【解析】在△ABC中,因为EF∥AB,所以
在△DBC中,因为EF∥CD,所以
两式相加,得
所以 故EF=
答案:19.如图,梯形ADHE中,AE∥BF∥CG∥DH,AB= BC=CD,AE=12,DH=16,AH交BF于M,则BM=____,CG=____.【解析】∵AE∥BF∥CG∥DH,AB= BC=CD,AE=12,DH=16,∴ ∴ ∴BM=4.
取BC的中点P,作PQ∥DH交EH于Q,如图,则PQ是梯形ADHE的中位线,∴PQ= (AE+DH)= (12+16)=14.同理:CG= (PQ+DH)= (14+16)=15.
答案: 4 1520.如图,已知AD∥EG∥BC,AD=6,BC=9, 则GF的长
为____.【解析】∵AD∥EG∥BC,
∴
∵ ∴ ∴
又∵AD=6,BC=9,∴EF=2,EG=6,
∴GF=EG-EF=4.
答案:421.(2013·三亚模拟)如图所示,身高为1.6米的某学生想测量学校旗杆的高度,当他站在C处时,他的影子的顶端正好与旗杆影子的顶端重合,并测得AC=2米,BC=8米,则旗杆的高度是____米.【解析】由题意,知CD∥BE.∴△ACD∽△ABE,
∴ ∵AC=2米,BC=8米,∴AB=10米.
又∵CD=1.6米,∴ ∴BE=8米.
答案:822.如图,在△ABC中,DE∥BC,
EF∥CD,且AB=2,AD= 则AF=____.
【解析】∵DE∥BC,∴
∵EF∥CD,∴
∴ ∴AD2=AF·AB.
∵AB=2,AD= ∴AF=1.
答案:123.在矩形ABCD中,AE⊥BD于E,矩形的面积为40 cm2, S△ABE∶S△DBA=1∶5,则AE的长为 ____cm.【解析】∵S△ABE∶S△DBA=1∶5,
∴S△ABE∶S矩形ABCD=1∶10,
∴S△ABE= S矩形ABCD= ×40=4(cm2).
由△ABE∽△DAE易证相似比为1∶2,
即BE∶AE=1∶2,
设BE=x cm,则AE=2x cm,
∴ x·2x=4,∴x=2,∴AE=4 cm.
答案:424.如图,在梯形ABCD中,AD∥BC,BD,AC相交于O.过O的直线分别交AB,CD于E,F,且EF∥BC,若AD=12,BC=20,则EF=___.【解析】∵EF∥BC,AD=12,BC=20,
∴
∵OE∥BC,∴ ∴OE=
∵OF∥AD,∴ ∴OF=
∴EF=OE+OF= =15.
答案:1525.如图,ABCD为正方形,A,E,F,G在同一条直线上,且AE=6,EF=4,那么FG=____.【解析】∵DF∥AB,∴
∴
又∵CF∥AB,∴
即 ∴FG=5.
答案:5
