【全程复习方略】2014-2015学年高中数学理(人教广东版)教师配套课件选修4-4第一节坐标系(共75张PPT)
文档属性
| 名称 | 【全程复习方略】2014-2015学年高中数学理(人教广东版)教师配套课件选修4-4第一节坐标系(共75张PPT) |

|
|
| 格式 | zip | ||
| 文件大小 | 2.5MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教新课标A版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2014-12-26 00:00:00 | ||
图片预览










文档简介
课件75张PPT。选修4-4 坐标系与参数方程
第一节 坐 标 系1.平面直角坐标系中的坐标伸缩变换
设点P(x,y)是平面直角坐标系中的任意一点,在变换
φ:______________的作用下,点P(x,y)对应到点
P′(x′,y′),称φ为平面直角坐标系中的坐标伸缩变换,
简称伸缩变换. 2.极坐标系与点的极坐标
(1)极坐标系:在平面内取一个定点O,叫做_____,自极点O引一条射线Ox,叫做_____;再选定一个长度单位、一个角度单位(通常取弧度)及其正方向(通常取逆时针方向),就建立了极坐标系.
(2)点的极坐标:对于极坐标系所在平面内的任一点M,若设|OM|=ρ(ρ≥0),以极轴Ox为始边,射线OM为终边的角为θ,则点M可用有序数对________表示.极点极轴(ρ,θ)(3)极坐标与直角坐标的互化公式:
设点P的直角坐标为(x,y),它的极坐标为(ρ,θ),则相互转化公式为
3.直线的极坐标方程
(1)特殊位置的直线的极坐标方程:π+ααπ+αρcos θρsin θα(2)一般位置的直线的极坐标方程:若直线l经过点M(ρ0,
θ0),且极轴到此直线的角为α,直线l的极坐标方程为:
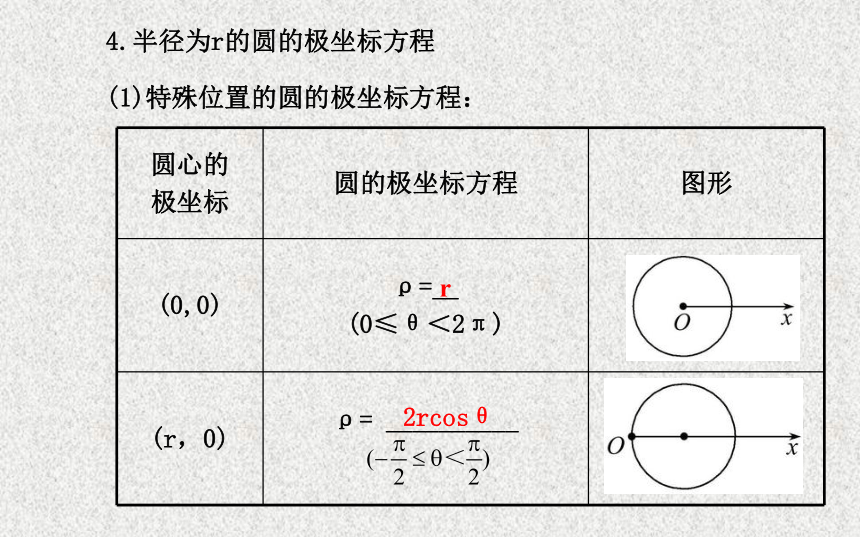
ρsin(α-θ)=_______________. ρ0sin(α-θ0)4.半径为r的圆的极坐标方程
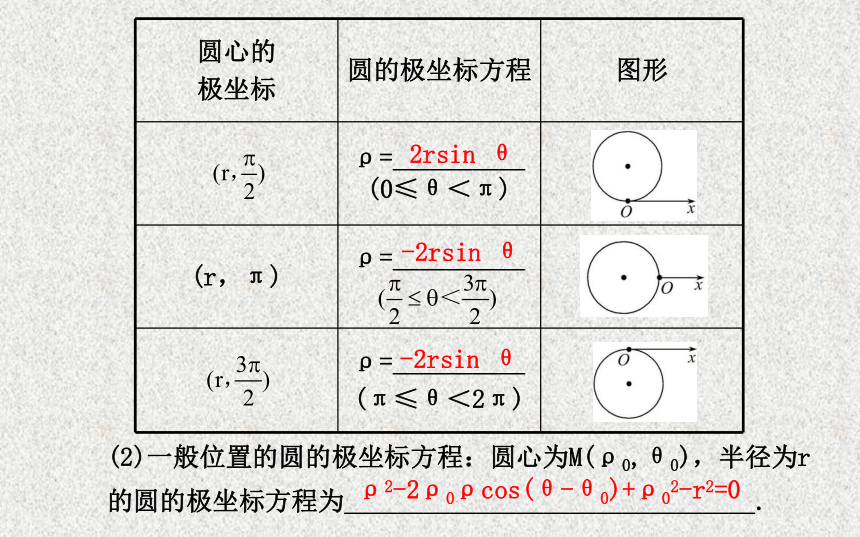
(1)特殊位置的圆的极坐标方程:r2rcosθ2rsin θ-2rsin θ-2rsin θ(2)一般位置的圆的极坐标方程:圆心为M(ρ0,θ0),半径为r
的圆的极坐标方程为_______________________________. ρ2-2ρ0ρcos(θ-θ0)+ρ02-r2=0判断下面结论是否正确(请在括号中打“√”或“×”).
(1)在极坐标系中,点M的坐标是惟一的.( )
(2)极坐标系所在平面内的点与极坐标是一一对应的关系.( )
(3)三角函数是联系极坐标与直角坐标的纽带.( )
(4)椭圆伸缩后仍是椭圆.( )【解析】(1)错误.极坐标系中的点,当θ∈[0,2π)时,除极点外,M的极坐标是惟一的,当θ∈R时,M的极坐标不惟一.
(2)错误.建立极坐标系后,给定(ρ,θ),就可以在平面内惟一确定一点M;反过来,给定平面内一点M,它的极坐标(ρ,θ)(θ∈R)却不是惟一的,所以二者不能建立一一对应关系.
(3)正确.由转化公式,根据任意角的三角函数的定义及其基本关系式,诱导公式,可以把二者联系起来.
(4)错误.变换系数λ与μ的值,伸缩后有可能为圆.
答案: (1)× (2)× (3)√ (4)×考向 1 伸缩变换公式及其应用
【典例1】(1)曲线x2+y2=1在伸缩变换φ: 作用下得到
曲线的焦距等于_______.
(2)若函数y=f(x)的图象在伸缩变换φ: 作用下得到曲
线的方程为 则函数y=f(x)的最小正周期
为_____.【思路点拨】(1)设变换前后的曲线上的点的坐标,利用代换法求出变换后的曲线方程再求解.
(2)求出函数y=f(x)的解析式,再求最小正周期即可.【规范解答】(1)设曲线x2+y2=1上任意一点的坐标为P(x,y),
在伸缩变换φ: 作用下得到曲线的对应点的坐标为
P′(x′,y′),将 代入曲线方程x2+y2=1,得
这是焦点在纵轴上的椭圆,其中a2=25,b2=16,所
以c2=a2-b2=9,所以2c=6.
答案: 6(2)设函数y=f(x)的图象上任意一点的坐标为P(x,y),在伸缩变换φ: 作用下得到点P的对应点的坐标为P′(x′,
y′),将φ: 代入曲线方程 得
即 所以函数y=f(x)的最小正周期为π.
答案: π【互动探究】本例(2)中,若改为“函数 的图象
在伸缩变换φ: 作用下得到曲线的方程
为 ”,则λ=______,μ=______.【解析】设函数 的图象上任意一点为P(x,y),在
伸缩变换φ的作用下得到曲线的对应点为P′(x′,y′),则
将其代入 得
∴
依题意,得
∴λ=2,μ=3.
答案: 2 3【拓展提升】求伸缩变换的曲线方程的解题思路
(1)曲线的伸缩变换是通过曲线上每一点的坐标的伸缩变换实
现的,解题时需要区分变换前的点P的坐标(x,y)与变换后的对
应点P′的坐标(x′,y′),再利用伸缩变换公式
建立联系即可.
(2)若已知变换前与变换后的曲线方程,则可以确定伸缩变换
公式,可以由相等函数的关系求λ,μ的值.【变式备选】
(1)将正弦曲线y=sin x按φ: 变换后的函数的值域
为______.【解析】设点P(x,y)为正弦曲线y=sin x上的任意一点,在变换 的作用下,点P(x,y)对应到点P′(x′,y′),
即
代入y=sin x得 ,
所以 即 所以函数的值域为[-3,3].
答案: [-3,3](2)将正弦曲线y=sin x变换为曲线y=2sin 3x的伸缩变换公式
为______.
【解析】将变换后的曲线y=2sin 3x改写为 由变换
前曲线为y=sin x得 即得伸缩变换公式
答案:考向 2 点的极坐标与直角坐标的转化
【典例2】(1)若点M的极坐标为 则点M的直角坐标为____.
(2)若ρ>0,θ∈[0,2π),直角坐标为 则点M的极坐标为______.
【思路点拨】(1)由公式 计算点的直角坐标.
(2)由公式 求M的极坐标.【规范解答】(1)由公式 得
∴点M的直角坐标为
答案:(2)由公式 得
∵点 在第四象限,且θ∈[0,2π),
∴
所以点M的极坐标为
答案:【拓展提升】直角坐标化为极坐标的不惟一性
(1)根据终边相同的角的意义,角θ的表示方法具有周期性,故点M的极坐标(ρ,θ)的形式不惟一,即一个点的极坐标有多种表达形式.
当限定ρ>0,θ∈[0,2π)时,除极点外,点M的极坐标是惟一的.
极点O的极坐标为(0,θ),θ为任意值,但一般取θ=0,即极点的极坐标为(0,0).(2)把点的直角坐标化为极坐标时,求极角θ应注意判断点P所在的象限(即角θ的终边的位置),以便正确地求出角θ.
【提醒】若没有特别要求,求出θ∈[0,2π)内的主值角即可.
【变式训练】(1)将点的极坐标 化为直角坐标为_____.
【解析】由公式 得
∴极坐标 化为直角坐标为(0,-1).
答案:(0,-1)(2)若ρ>0,θ∈R,将点的直角坐标(-1,-1)化为极坐标
为______.
【解析】由公式 得
∵点(-1,-1)在第三象限, ∴
所以点(-1,-1)的极坐标为
答案:考向 3 求曲线的极坐标方程
【典例3】(1)(2013·岳阳模拟)以极坐标系中的点 为圆
心,1为半径的圆的极坐标方程是______.
(2)(2012·上海高考)如图,在极坐标系中,过点M(2,0)的直
线l与极轴的夹角 若将l的极坐标方程写成ρ=f(θ)的形
式,则f(θ)=______.【思路点拨】(1)可以先求出圆的直角坐标方程,再化为极坐标方程,也可以结合图形解直角三角形直接得到圆的极坐标方程.
(2)先求直线的直角坐标方程,再化为极坐标方程,也可以利用正弦定理直接求直线的极坐标方程.【规范解答】(1)方法一:在极坐标系中,圆心 的直角坐标为 由半径为1,得圆的直角坐标方程为
即
由公式 得
即 为所求.方法二:设圆上任意一点的极坐标为M(ρ,θ),如图,
在△OMP中,
为所求.
答案:(2)方法一:在平面直角坐标系中,直线的倾斜角为 故直线
的斜率为 直线又过点(2,0),所以直线的方程为
由公式 得
即
化简,得 即 为所求.方法二:设直线上的任一点的极坐标为P(ρ,θ),
因为 所以
根据正弦定理得
即 即
答案:【拓展提升】求曲线方程的方法步骤
(1)求曲线方程,首先要根据条件建立适当的平面直角坐标系(或极坐标系).
(2)设出曲线上任意一点的坐标为M(x,y),找出此动点满足的几何条件,最后通过代数变换化简方程即可.
【提醒】在平面直角坐标系中,求曲线的轨迹方程的方法有直译法、定义法、相关点法.在极坐标系中,求曲线的极坐标方程以上几种方法仍然是适用的.【变式训练】如图,点A在直线x=3上移动,点O,P,A按顺时
针方向排列,等腰△OPA的顶角∠OPA为 则点P的轨迹的极
坐标方程为______.【解析】以O作为极点,Ox轴的正方向为极轴,建立极坐标
系,则直线x=3的极坐标方程为
设A(ρ0,θ0),P(ρ,θ).
∵点A在直线ρcos θ=3上,
∴ρ0cos θ0=3 ①,
∵△OPA为等腰三角形,且
代入①得 为所求.
答案: 考向 4 极坐标方程化为直角坐标方程
【典例4】(1)(2012·安徽高考)在极坐标系中,圆ρ=4sin θ
的圆心到直线 的距离是______.
(2)在极坐标系下,直线 与圆 的公共点个
数是______.【思路点拨】(1)先求直线与圆的直角坐标方程,再用点到直线的距离公式计算.
(2)先求直线与圆的直角坐标方程,再判断直线与圆的位置关系即可求得.【规范解答】(1)圆ρ=4sin θ,即x2+(y-2)2=4的圆心为C(0,2),直线l:
点C到直线l的距离是
答案: (2)直线 即ρcos θ+ρsin θ=2,
故直角坐标方程为x+y=2.
圆 的直角坐标方程为x2+y2=2,
圆心(0,0)到直线x+y=2的距离满足
即直线与圆相切,所以直线与圆的公共点个数是1.
答案: 1【拓展提升】极坐标方程与直角坐标方程的转化公式
由公式 可以将极坐标方程化为直角坐标方程,由
公式 可以将直角坐标方程化为极坐标方程.
【提醒】注意曲线方程互相转化时的等价性.【变式训练】(1)极坐标系中,直线l的方程为ρsin θ=4,则点
到直线l的距离为______.
【解析】直线l:ρsin θ=4的直角坐标方程为y=4,点
的直角坐标为 则点到直线l的距离为3.
答案: 3(2)在极坐标系中,圆 上的点与直线
的最大距离是______.
【解析】圆的极坐标方程
即ρ2=-2ρsin θ,化为直角坐标方程为x2+y2+2y=0,配方,
得x2+(y+1)2=1,
可得圆心为(0,-1),半径为1.直线的极坐标方程
即ρcos θ+ρsin θ=2
化为直角坐标方程为x+y-2=0,
圆心(0,-1)到此直线的距离为
所以直线与圆相离,所以圆上的点与直线的最大距离是
答案: 1.直线ρcos θ=3的倾斜角等于______.
【解析】直线ρcos θ=3的直角坐标方程为x=3,所以直线的
倾斜角为
答案:2.(2013·丰台模拟)在极坐标系中,圆ρ=2sin θ的圆心的
极坐标是______.
【解析】方法一:圆ρ=2sin θ的圆心为
方法二:圆ρ=2sin θ的直角坐标方程为x2+y2=2y,圆心坐标
为(0,1),化为极坐标为
答案: 3.在极坐标系中,圆C的极坐标方程为
则圆心的极坐标为______.
【解析】∵圆的极坐标方程是
即
则该圆的直角坐标方程为
即
它表示以 为圆心,半径等于2的圆,
∴该圆的圆心的极坐标是
答案:4.极坐标方程ρ2cos θ-ρ=0(ρ≥0)化为直角坐标方程
为_____.
【解析】极坐标方程ρ2cos θ-ρ=0为ρ(ρcos θ-1)=0,
∴ρ=0或ρcos θ=1.
所以直角坐标方程为x2+y2=0或x=1.
答案: x2+y2=0或x=15.曲线ρ=4cos θ关于直线 对称的曲线的极坐标方程
为______.
【解析】设所求曲线上任意一点的极坐标为P(ρ,θ),它关
于直线 对称的点的坐标为 代入ρ=4cos θ,
得 即ρ=4sin θ.
答案: ρ=4sin θ6.在极坐标系中,点 与 之间的距离为______.
【解析】方法一:点 与 的直角坐标分别为
与 于是
方法二:由点 与 知,|OA|=|OB|=2,
于是△AOB为等边三角形,所以|AB|=2.
答案: 27.在极坐标系中,点(1,0)到直线ρ(cos θ+sin θ)=2的距
离为______.
【解析】直线ρ(cos θ+sin θ)=2的直角坐标方程为x+y-
2=0,极坐标(1,0)的直角坐标为(1,0),而点(1,0)到该直线
的距离为
答案: 8.若点P(-2 013,2 014)经过伸缩变换 后的点在
曲线x′y′=k上,则k=______.
【解析】∵P(-2 013,2 014)经过伸缩变换
得k=x′y′=-1.
答案: -19.圆ρ=6cos θ的面积等于______.
【解析】由公式 ρ2=x2+y2得
圆ρ=6cos θ的直角坐标方程为x2+y2=6x,其标准方程为
(x-3)2+y2=9,所以圆的半径r=3,圆的面积等于S=πr2=9π.
答案: 9π10.圆x2+y2=1经过伸缩变换 后的曲线的焦距为______.
【解析】由
得
代入x2+y2=1,得
即 所以焦距为
答案: 11.在极坐标系中,曲线ρ(cos θ+sin θ)=1与ρ(sin θ-
cos θ)=1(θ∈[0,2π))的交点的极坐标为______.
【解析】曲线ρ(cos θ+sin θ)=1与ρ(sin θ-cos θ)=1的
直角坐标方程分别为x+y=1和y-x=1,两条直线的交点的直角坐
标为(0,1),化为极坐标为
答案:12.极坐标系中,ρ≥0,过极点倾斜角为 的直线的极坐标
方程为______.
【解析】以极点O为端点,所求直线上点的极坐标分成两条射
线,两条射线的极坐标方程分别为 所以过极点
倾斜角为 的直线的极坐标方程为
答案: 13.在极坐标系中,点 关于直线l:ρcos θ=1的对称点
的一个极坐标为______.
【解析】以极点为原点,极轴所在直线为x轴,
建立直角坐标系,则由公式 得
点 的直角坐标为(0,2),
直线l:ρcos θ=1的直角坐标方程为x=1,
点(0,2)关于直线l:x=1的对称点的坐标为(2,2),利用公式
得ρ2=x2+y2=8,
因为角θ的终边过点(2,2),故
所以点的直角坐标(2,2)化为极坐标为
答案:14.限定ρ≥0,0≤θ<2π,若点M的直角坐标是 则点M
的极坐标为______.
【解析】∵
且点 在第二象限,
答案:15.将正弦曲线y=sin x按伸缩变换 后得到曲线方程的
振幅为______,最小正周期为______.
【解析】由
代入曲线y=sin x,得 即
故振幅为3,最小正周期为4π.
答案: 3 4π16.在极坐标系中,O为极点,设点 则△OAB
的面积为______.
【解析】点 即 且点
所以△OAB的面积为
答案:517.已知极坐标系的极点在直角坐标系的原点,极轴与x轴的正
半轴重合,曲线C的直角坐标方程 化为极坐
标方程为______.
【解析】由 得,
∴
得
答案:18.在极坐标系中,若O是极点, 则三角形OAB的
面积S△OAB=______.
【解析】在极坐标系中画出点A,B,易得∠AOB=150°.
在△OAB中,
答案: 19.曲线的极坐标方程ρ=4cos θ化为直角坐标方程为______.
【解析】将原极坐标方程ρ=4cos θ化为:
ρ2=4ρcos θ,
化成直角坐标方程为:x2+y2-4x=0,
即(x-2)2+y2=4.
答案: (x-2)2+y2=420.在极坐标系中,点 到圆ρ=2cos θ的圆心的距离
为______.
【解析】由x=ρcos θ,y=ρsin θ及ρ=2cos θ,
得x=2cos2θ,y=2cos θsin θ,
则x=1+cos 2θ,y=sin 2θ,所以(x-1)2+y2=1,即圆心坐标
为(1,0),而点 在直角坐标系中的坐标为 所以所
求的距离为
答案:21.若圆的极坐标方程为ρ2-2ρcos θ+4ρsin θ+4=0,则圆
的半径r=______.
【解析】圆的极坐标方程ρ2-2ρcos θ+4ρsin θ+4=0化为
直角坐标方程为x2+y2-2x+4y+4=0,
即(x-1)2+(y+2)2=1,所以圆的半径为1.
答案:122.(2013·珠海模拟)在极坐标系中,圆ρ=2cos θ的圆心到
直线ρcos θ=2的距离是______.
【解析】圆ρ=2cos θ的直角坐标方程为x2+y2=2x,直线
ρcos θ=2的直角坐标方程为x=2,所以圆心(1,0)到直线
x=2的距离为1.
答案:123.极坐标系下,圆 上的点与直线
的最小距离是______.
【解析】圆的极坐标方程 即
化为直角坐标方程为
配方,得 圆心为 半径为1.直线的极坐标方程 即ρcos θ+ρsin θ=2,
化为直角坐标方程为x+y-2=0,圆心 到此直线的距
离为 所以直线与圆相离,所以圆上的点
与直线的最小距离是
答案: 24.已知圆O1和圆O2的极坐标方程分别为ρ=4cos θ,
ρ=-sin θ,则经过圆O1与圆O2两个交点的直线的直角坐标方
程为______.
【解析】以极点为原点,极轴为x轴正半轴,建立平面直角坐
标系,两坐标系中取相同的长度单位.
由公式x=ρcos θ,y=ρsin θ,
将ρ=4cos θ化为ρ2=4ρcos θ,
∴x2+y2=4x.即x2+y2-4x=0为圆O1的直角坐标方程.
同理x2+y2+y=0为圆O2的直角坐标方程.
由 相减,得过交点的直线的直角坐标方程为
4x+y=0.
答案:4x+y=025.在极坐标系中,圆ρ=2cos θ与直线3ρcos θ+4ρsin θ
+a=0相切,则实数a=______.
【解析】由圆ρ=2cos θ得ρ2=2ρcos θ,
∵
∴ρ2=x2+y2,
所以圆ρ=2cos θ与直线3ρcos θ+4ρsin θ+a=0的直角坐
标方程分别为x2+y2=2x,3x+4y+a=0. 将圆的方程配方得(x-1)2+y2=1,
依题意,得圆心C(1,0)到直线的距离为1,
即 整理,得|3+a|=5,
解得a=2或a=-8.
答案:2或-8
第一节 坐 标 系1.平面直角坐标系中的坐标伸缩变换
设点P(x,y)是平面直角坐标系中的任意一点,在变换
φ:______________的作用下,点P(x,y)对应到点
P′(x′,y′),称φ为平面直角坐标系中的坐标伸缩变换,
简称伸缩变换. 2.极坐标系与点的极坐标
(1)极坐标系:在平面内取一个定点O,叫做_____,自极点O引一条射线Ox,叫做_____;再选定一个长度单位、一个角度单位(通常取弧度)及其正方向(通常取逆时针方向),就建立了极坐标系.
(2)点的极坐标:对于极坐标系所在平面内的任一点M,若设|OM|=ρ(ρ≥0),以极轴Ox为始边,射线OM为终边的角为θ,则点M可用有序数对________表示.极点极轴(ρ,θ)(3)极坐标与直角坐标的互化公式:
设点P的直角坐标为(x,y),它的极坐标为(ρ,θ),则相互转化公式为
3.直线的极坐标方程
(1)特殊位置的直线的极坐标方程:π+ααπ+αρcos θρsin θα(2)一般位置的直线的极坐标方程:若直线l经过点M(ρ0,
θ0),且极轴到此直线的角为α,直线l的极坐标方程为:
ρsin(α-θ)=_______________. ρ0sin(α-θ0)4.半径为r的圆的极坐标方程
(1)特殊位置的圆的极坐标方程:r2rcosθ2rsin θ-2rsin θ-2rsin θ(2)一般位置的圆的极坐标方程:圆心为M(ρ0,θ0),半径为r
的圆的极坐标方程为_______________________________. ρ2-2ρ0ρcos(θ-θ0)+ρ02-r2=0判断下面结论是否正确(请在括号中打“√”或“×”).
(1)在极坐标系中,点M的坐标是惟一的.( )
(2)极坐标系所在平面内的点与极坐标是一一对应的关系.( )
(3)三角函数是联系极坐标与直角坐标的纽带.( )
(4)椭圆伸缩后仍是椭圆.( )【解析】(1)错误.极坐标系中的点,当θ∈[0,2π)时,除极点外,M的极坐标是惟一的,当θ∈R时,M的极坐标不惟一.
(2)错误.建立极坐标系后,给定(ρ,θ),就可以在平面内惟一确定一点M;反过来,给定平面内一点M,它的极坐标(ρ,θ)(θ∈R)却不是惟一的,所以二者不能建立一一对应关系.
(3)正确.由转化公式,根据任意角的三角函数的定义及其基本关系式,诱导公式,可以把二者联系起来.
(4)错误.变换系数λ与μ的值,伸缩后有可能为圆.
答案: (1)× (2)× (3)√ (4)×考向 1 伸缩变换公式及其应用
【典例1】(1)曲线x2+y2=1在伸缩变换φ: 作用下得到
曲线的焦距等于_______.
(2)若函数y=f(x)的图象在伸缩变换φ: 作用下得到曲
线的方程为 则函数y=f(x)的最小正周期
为_____.【思路点拨】(1)设变换前后的曲线上的点的坐标,利用代换法求出变换后的曲线方程再求解.
(2)求出函数y=f(x)的解析式,再求最小正周期即可.【规范解答】(1)设曲线x2+y2=1上任意一点的坐标为P(x,y),
在伸缩变换φ: 作用下得到曲线的对应点的坐标为
P′(x′,y′),将 代入曲线方程x2+y2=1,得
这是焦点在纵轴上的椭圆,其中a2=25,b2=16,所
以c2=a2-b2=9,所以2c=6.
答案: 6(2)设函数y=f(x)的图象上任意一点的坐标为P(x,y),在伸缩变换φ: 作用下得到点P的对应点的坐标为P′(x′,
y′),将φ: 代入曲线方程 得
即 所以函数y=f(x)的最小正周期为π.
答案: π【互动探究】本例(2)中,若改为“函数 的图象
在伸缩变换φ: 作用下得到曲线的方程
为 ”,则λ=______,μ=______.【解析】设函数 的图象上任意一点为P(x,y),在
伸缩变换φ的作用下得到曲线的对应点为P′(x′,y′),则
将其代入 得
∴
依题意,得
∴λ=2,μ=3.
答案: 2 3【拓展提升】求伸缩变换的曲线方程的解题思路
(1)曲线的伸缩变换是通过曲线上每一点的坐标的伸缩变换实
现的,解题时需要区分变换前的点P的坐标(x,y)与变换后的对
应点P′的坐标(x′,y′),再利用伸缩变换公式
建立联系即可.
(2)若已知变换前与变换后的曲线方程,则可以确定伸缩变换
公式,可以由相等函数的关系求λ,μ的值.【变式备选】
(1)将正弦曲线y=sin x按φ: 变换后的函数的值域
为______.【解析】设点P(x,y)为正弦曲线y=sin x上的任意一点,在变换 的作用下,点P(x,y)对应到点P′(x′,y′),
即
代入y=sin x得 ,
所以 即 所以函数的值域为[-3,3].
答案: [-3,3](2)将正弦曲线y=sin x变换为曲线y=2sin 3x的伸缩变换公式
为______.
【解析】将变换后的曲线y=2sin 3x改写为 由变换
前曲线为y=sin x得 即得伸缩变换公式
答案:考向 2 点的极坐标与直角坐标的转化
【典例2】(1)若点M的极坐标为 则点M的直角坐标为____.
(2)若ρ>0,θ∈[0,2π),直角坐标为 则点M的极坐标为______.
【思路点拨】(1)由公式 计算点的直角坐标.
(2)由公式 求M的极坐标.【规范解答】(1)由公式 得
∴点M的直角坐标为
答案:(2)由公式 得
∵点 在第四象限,且θ∈[0,2π),
∴
所以点M的极坐标为
答案:【拓展提升】直角坐标化为极坐标的不惟一性
(1)根据终边相同的角的意义,角θ的表示方法具有周期性,故点M的极坐标(ρ,θ)的形式不惟一,即一个点的极坐标有多种表达形式.
当限定ρ>0,θ∈[0,2π)时,除极点外,点M的极坐标是惟一的.
极点O的极坐标为(0,θ),θ为任意值,但一般取θ=0,即极点的极坐标为(0,0).(2)把点的直角坐标化为极坐标时,求极角θ应注意判断点P所在的象限(即角θ的终边的位置),以便正确地求出角θ.
【提醒】若没有特别要求,求出θ∈[0,2π)内的主值角即可.
【变式训练】(1)将点的极坐标 化为直角坐标为_____.
【解析】由公式 得
∴极坐标 化为直角坐标为(0,-1).
答案:(0,-1)(2)若ρ>0,θ∈R,将点的直角坐标(-1,-1)化为极坐标
为______.
【解析】由公式 得
∵点(-1,-1)在第三象限, ∴
所以点(-1,-1)的极坐标为
答案:考向 3 求曲线的极坐标方程
【典例3】(1)(2013·岳阳模拟)以极坐标系中的点 为圆
心,1为半径的圆的极坐标方程是______.
(2)(2012·上海高考)如图,在极坐标系中,过点M(2,0)的直
线l与极轴的夹角 若将l的极坐标方程写成ρ=f(θ)的形
式,则f(θ)=______.【思路点拨】(1)可以先求出圆的直角坐标方程,再化为极坐标方程,也可以结合图形解直角三角形直接得到圆的极坐标方程.
(2)先求直线的直角坐标方程,再化为极坐标方程,也可以利用正弦定理直接求直线的极坐标方程.【规范解答】(1)方法一:在极坐标系中,圆心 的直角坐标为 由半径为1,得圆的直角坐标方程为
即
由公式 得
即 为所求.方法二:设圆上任意一点的极坐标为M(ρ,θ),如图,
在△OMP中,
为所求.
答案:(2)方法一:在平面直角坐标系中,直线的倾斜角为 故直线
的斜率为 直线又过点(2,0),所以直线的方程为
由公式 得
即
化简,得 即 为所求.方法二:设直线上的任一点的极坐标为P(ρ,θ),
因为 所以
根据正弦定理得
即 即
答案:【拓展提升】求曲线方程的方法步骤
(1)求曲线方程,首先要根据条件建立适当的平面直角坐标系(或极坐标系).
(2)设出曲线上任意一点的坐标为M(x,y),找出此动点满足的几何条件,最后通过代数变换化简方程即可.
【提醒】在平面直角坐标系中,求曲线的轨迹方程的方法有直译法、定义法、相关点法.在极坐标系中,求曲线的极坐标方程以上几种方法仍然是适用的.【变式训练】如图,点A在直线x=3上移动,点O,P,A按顺时
针方向排列,等腰△OPA的顶角∠OPA为 则点P的轨迹的极
坐标方程为______.【解析】以O作为极点,Ox轴的正方向为极轴,建立极坐标
系,则直线x=3的极坐标方程为
设A(ρ0,θ0),P(ρ,θ).
∵点A在直线ρcos θ=3上,
∴ρ0cos θ0=3 ①,
∵△OPA为等腰三角形,且
代入①得 为所求.
答案: 考向 4 极坐标方程化为直角坐标方程
【典例4】(1)(2012·安徽高考)在极坐标系中,圆ρ=4sin θ
的圆心到直线 的距离是______.
(2)在极坐标系下,直线 与圆 的公共点个
数是______.【思路点拨】(1)先求直线与圆的直角坐标方程,再用点到直线的距离公式计算.
(2)先求直线与圆的直角坐标方程,再判断直线与圆的位置关系即可求得.【规范解答】(1)圆ρ=4sin θ,即x2+(y-2)2=4的圆心为C(0,2),直线l:
点C到直线l的距离是
答案: (2)直线 即ρcos θ+ρsin θ=2,
故直角坐标方程为x+y=2.
圆 的直角坐标方程为x2+y2=2,
圆心(0,0)到直线x+y=2的距离满足
即直线与圆相切,所以直线与圆的公共点个数是1.
答案: 1【拓展提升】极坐标方程与直角坐标方程的转化公式
由公式 可以将极坐标方程化为直角坐标方程,由
公式 可以将直角坐标方程化为极坐标方程.
【提醒】注意曲线方程互相转化时的等价性.【变式训练】(1)极坐标系中,直线l的方程为ρsin θ=4,则点
到直线l的距离为______.
【解析】直线l:ρsin θ=4的直角坐标方程为y=4,点
的直角坐标为 则点到直线l的距离为3.
答案: 3(2)在极坐标系中,圆 上的点与直线
的最大距离是______.
【解析】圆的极坐标方程
即ρ2=-2ρsin θ,化为直角坐标方程为x2+y2+2y=0,配方,
得x2+(y+1)2=1,
可得圆心为(0,-1),半径为1.直线的极坐标方程
即ρcos θ+ρsin θ=2
化为直角坐标方程为x+y-2=0,
圆心(0,-1)到此直线的距离为
所以直线与圆相离,所以圆上的点与直线的最大距离是
答案: 1.直线ρcos θ=3的倾斜角等于______.
【解析】直线ρcos θ=3的直角坐标方程为x=3,所以直线的
倾斜角为
答案:2.(2013·丰台模拟)在极坐标系中,圆ρ=2sin θ的圆心的
极坐标是______.
【解析】方法一:圆ρ=2sin θ的圆心为
方法二:圆ρ=2sin θ的直角坐标方程为x2+y2=2y,圆心坐标
为(0,1),化为极坐标为
答案: 3.在极坐标系中,圆C的极坐标方程为
则圆心的极坐标为______.
【解析】∵圆的极坐标方程是
即
则该圆的直角坐标方程为
即
它表示以 为圆心,半径等于2的圆,
∴该圆的圆心的极坐标是
答案:4.极坐标方程ρ2cos θ-ρ=0(ρ≥0)化为直角坐标方程
为_____.
【解析】极坐标方程ρ2cos θ-ρ=0为ρ(ρcos θ-1)=0,
∴ρ=0或ρcos θ=1.
所以直角坐标方程为x2+y2=0或x=1.
答案: x2+y2=0或x=15.曲线ρ=4cos θ关于直线 对称的曲线的极坐标方程
为______.
【解析】设所求曲线上任意一点的极坐标为P(ρ,θ),它关
于直线 对称的点的坐标为 代入ρ=4cos θ,
得 即ρ=4sin θ.
答案: ρ=4sin θ6.在极坐标系中,点 与 之间的距离为______.
【解析】方法一:点 与 的直角坐标分别为
与 于是
方法二:由点 与 知,|OA|=|OB|=2,
于是△AOB为等边三角形,所以|AB|=2.
答案: 27.在极坐标系中,点(1,0)到直线ρ(cos θ+sin θ)=2的距
离为______.
【解析】直线ρ(cos θ+sin θ)=2的直角坐标方程为x+y-
2=0,极坐标(1,0)的直角坐标为(1,0),而点(1,0)到该直线
的距离为
答案: 8.若点P(-2 013,2 014)经过伸缩变换 后的点在
曲线x′y′=k上,则k=______.
【解析】∵P(-2 013,2 014)经过伸缩变换
得k=x′y′=-1.
答案: -19.圆ρ=6cos θ的面积等于______.
【解析】由公式 ρ2=x2+y2得
圆ρ=6cos θ的直角坐标方程为x2+y2=6x,其标准方程为
(x-3)2+y2=9,所以圆的半径r=3,圆的面积等于S=πr2=9π.
答案: 9π10.圆x2+y2=1经过伸缩变换 后的曲线的焦距为______.
【解析】由
得
代入x2+y2=1,得
即 所以焦距为
答案: 11.在极坐标系中,曲线ρ(cos θ+sin θ)=1与ρ(sin θ-
cos θ)=1(θ∈[0,2π))的交点的极坐标为______.
【解析】曲线ρ(cos θ+sin θ)=1与ρ(sin θ-cos θ)=1的
直角坐标方程分别为x+y=1和y-x=1,两条直线的交点的直角坐
标为(0,1),化为极坐标为
答案:12.极坐标系中,ρ≥0,过极点倾斜角为 的直线的极坐标
方程为______.
【解析】以极点O为端点,所求直线上点的极坐标分成两条射
线,两条射线的极坐标方程分别为 所以过极点
倾斜角为 的直线的极坐标方程为
答案: 13.在极坐标系中,点 关于直线l:ρcos θ=1的对称点
的一个极坐标为______.
【解析】以极点为原点,极轴所在直线为x轴,
建立直角坐标系,则由公式 得
点 的直角坐标为(0,2),
直线l:ρcos θ=1的直角坐标方程为x=1,
点(0,2)关于直线l:x=1的对称点的坐标为(2,2),利用公式
得ρ2=x2+y2=8,
因为角θ的终边过点(2,2),故
所以点的直角坐标(2,2)化为极坐标为
答案:14.限定ρ≥0,0≤θ<2π,若点M的直角坐标是 则点M
的极坐标为______.
【解析】∵
且点 在第二象限,
答案:15.将正弦曲线y=sin x按伸缩变换 后得到曲线方程的
振幅为______,最小正周期为______.
【解析】由
代入曲线y=sin x,得 即
故振幅为3,最小正周期为4π.
答案: 3 4π16.在极坐标系中,O为极点,设点 则△OAB
的面积为______.
【解析】点 即 且点
所以△OAB的面积为
答案:517.已知极坐标系的极点在直角坐标系的原点,极轴与x轴的正
半轴重合,曲线C的直角坐标方程 化为极坐
标方程为______.
【解析】由 得,
∴
得
答案:18.在极坐标系中,若O是极点, 则三角形OAB的
面积S△OAB=______.
【解析】在极坐标系中画出点A,B,易得∠AOB=150°.
在△OAB中,
答案: 19.曲线的极坐标方程ρ=4cos θ化为直角坐标方程为______.
【解析】将原极坐标方程ρ=4cos θ化为:
ρ2=4ρcos θ,
化成直角坐标方程为:x2+y2-4x=0,
即(x-2)2+y2=4.
答案: (x-2)2+y2=420.在极坐标系中,点 到圆ρ=2cos θ的圆心的距离
为______.
【解析】由x=ρcos θ,y=ρsin θ及ρ=2cos θ,
得x=2cos2θ,y=2cos θsin θ,
则x=1+cos 2θ,y=sin 2θ,所以(x-1)2+y2=1,即圆心坐标
为(1,0),而点 在直角坐标系中的坐标为 所以所
求的距离为
答案:21.若圆的极坐标方程为ρ2-2ρcos θ+4ρsin θ+4=0,则圆
的半径r=______.
【解析】圆的极坐标方程ρ2-2ρcos θ+4ρsin θ+4=0化为
直角坐标方程为x2+y2-2x+4y+4=0,
即(x-1)2+(y+2)2=1,所以圆的半径为1.
答案:122.(2013·珠海模拟)在极坐标系中,圆ρ=2cos θ的圆心到
直线ρcos θ=2的距离是______.
【解析】圆ρ=2cos θ的直角坐标方程为x2+y2=2x,直线
ρcos θ=2的直角坐标方程为x=2,所以圆心(1,0)到直线
x=2的距离为1.
答案:123.极坐标系下,圆 上的点与直线
的最小距离是______.
【解析】圆的极坐标方程 即
化为直角坐标方程为
配方,得 圆心为 半径为1.直线的极坐标方程 即ρcos θ+ρsin θ=2,
化为直角坐标方程为x+y-2=0,圆心 到此直线的距
离为 所以直线与圆相离,所以圆上的点
与直线的最小距离是
答案: 24.已知圆O1和圆O2的极坐标方程分别为ρ=4cos θ,
ρ=-sin θ,则经过圆O1与圆O2两个交点的直线的直角坐标方
程为______.
【解析】以极点为原点,极轴为x轴正半轴,建立平面直角坐
标系,两坐标系中取相同的长度单位.
由公式x=ρcos θ,y=ρsin θ,
将ρ=4cos θ化为ρ2=4ρcos θ,
∴x2+y2=4x.即x2+y2-4x=0为圆O1的直角坐标方程.
同理x2+y2+y=0为圆O2的直角坐标方程.
由 相减,得过交点的直线的直角坐标方程为
4x+y=0.
答案:4x+y=025.在极坐标系中,圆ρ=2cos θ与直线3ρcos θ+4ρsin θ
+a=0相切,则实数a=______.
【解析】由圆ρ=2cos θ得ρ2=2ρcos θ,
∵
∴ρ2=x2+y2,
所以圆ρ=2cos θ与直线3ρcos θ+4ρsin θ+a=0的直角坐
标方程分别为x2+y2=2x,3x+4y+a=0. 将圆的方程配方得(x-1)2+y2=1,
依题意,得圆心C(1,0)到直线的距离为1,
即 整理,得|3+a|=5,
解得a=2或a=-8.
答案:2或-8
