人教版数学七下 5.3.1平行线的性质 同步检测(含答案)
文档属性
| 名称 | 人教版数学七下 5.3.1平行线的性质 同步检测(含答案) |

|
|
| 格式 | docx | ||
| 文件大小 | 84.0KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-09-12 00:00:00 | ||
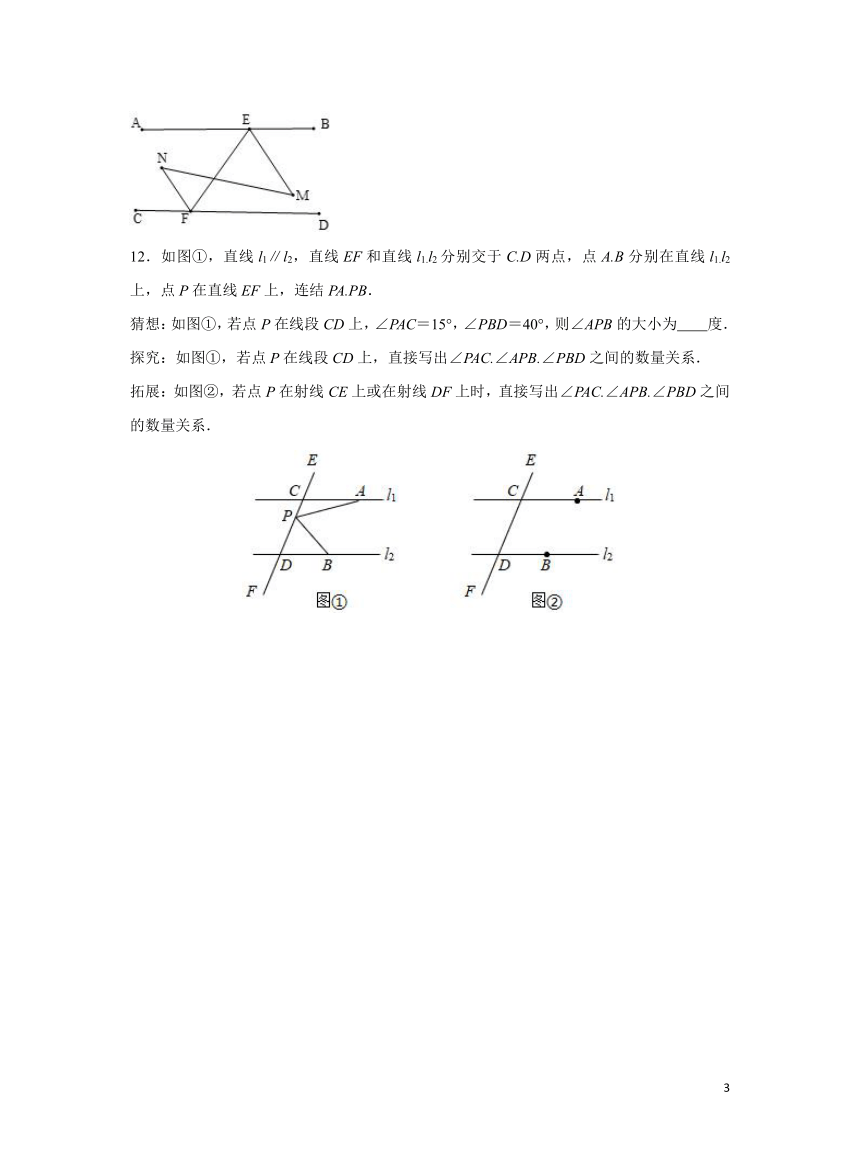
图片预览


文档简介
5.3.1平行线的性质
一、选择题
1.下列说法:①两直线平行,同旁内角互补;②内错角相等,两直线平行;③同位角相等,两直线平行;④垂直于同一条直线的两条直线平行,其中是平行线的性质的是 ( )
A.① B.②和③ C.④ D.①和④
2.如图,若AD∥BC,则下列结论正确的是( )
A.∠1=∠3 B.∠2=∠4 C.∠1=∠2 D.∠2=∠3
3.如图,a∥b,∠ABD的平分线交直线a于点C,CE⊥直线c于点E,∠1=24°,则∠2的大小为( )
A.114° B.142° C.147° D.156°
4.如图所示,直线l1//l2,∠1=40°,∠2=75°,则∠3等于( )
A.55° B.30° C.65° D.70°
二、填空题
5.如图,在四边形ABCD中,若∠A+∠B=180°,则∠C+∠D=_______.
6.将两张矩形纸片如图所示摆放,使其中一张矩形纸片的一个顶点恰好落在另一张矩形纸片的一条边上,则∠1+∠2=________.
7.如图,把一把直尺放在含30度角的直角三角板上,量得∠1=56°,则∠2的度数是 .
8.如图,已知AD∥BC,BD 平分∠ABC,∠A=112°,且BD⊥CD,则∠ADC= .
三、解答题
9.如图,直线AB∥CD,BC平分∠ABD,∠1=70°,求∠2的度数.
10.如图,直线EF∥GH,点A在EF上,AC交GH于点B,若∠FAC=72°,∠ACD=58°,点D在GH上,求∠BDC的度数.
11.如图,已知 ∠BEF+∠EFD=180°,EM平分∠BEF,FN平分∠EFC,求证:∠M=∠N.
12.如图①,直线l1∥l2,直线EF和直线l1.l2分别交于C.D两点,点A.B分别在直线l1.l2上,点P在直线EF上,连结PA.PB.
猜想:如图①,若点P在线段CD上,∠PAC=15°,∠PBD=40°,则∠APB的大小为 度.
探究:如图①,若点P在线段CD上,直接写出∠PAC.∠APB.∠PBD之间的数量关系.
拓展:如图②,若点P在射线CE上或在射线DF上时,直接写出∠PAC.∠APB.∠PBD之间的数量关系.
参考答案
一、选择题
1. 【答案】A;
【解析】两直线平行角的关系.
2.【答案】A;
【解析】∵AD∥BC,
∴∠3=∠1,
故选:A.
3.【答案】C;
【解析】∵∠1=24°,CE⊥直线c于点E,
∴∠EAC=90°﹣∠1=90°﹣24°=66°,
∵a∥b,
∴∠EAC=∠ABD=66°,
∵∠ABD的平分线交直线a于点C,
∴∠CBD,
∴∠2=180°﹣∠CBD=180°﹣33°=147°,
故选:C.
4.【答案】C;
【解析】∠3=180°-40°-75°=65°.
二、填空题
5.【答案】180°;
【解析】由已知可得:AD∥BC,由平行的性质可得:∠D+∠C=180°.
【答案】90°;
7.【答案】116°;
【解析】∵把一把直尺放在含30度角的直角三角板上,
∴a∥b,
∴∠1=∠3=56°,
∴∠4=180°﹣∠3=180°﹣56°=124°,
∴∠5=360°﹣∠4﹣90°﹣30°=360°﹣124°﹣90°﹣30°=116°,
∴∠2=∠5=116°,
故答案为:116°.
8.【答案】124°;
【解析】解:∵AD∥BC,∠A=112°,
∴∠ABC=180°﹣∠A=68°,
∵BD 平分∠ABC,
∴∠CBD∠ABC=34°,
∵BD⊥CD,
∴∠C=90°﹣∠CBD=56°,
∴∠ADC=180°﹣∠C=124°.
故答案为:124°.
三、解答题
9.【解析】
解:∵AB∥CD,
∴∠ABC=∠1=70°,∠ABD+∠BDC=180°,
∵BC平分∠ABD,
∴∠ABD=2∠ABC=140°,
∴∠BDC=180°﹣∠ABD=40°,
∴∠2=∠BDC=40°.
10.【解析】
解:∵EF∥GH,∴∠ABD+∠FAC=180°,∴∠ABD=180°﹣72°=108°,∵∠ABD=∠ACD+∠BDC,∴∠BDC=∠ABD﹣∠ACD=108°﹣58°=50°.
11.【解析】
解:∵∠BEF+∠EFD=180°,∴AB∥CD,∴∠BEF=∠EFC.
∵EM平分∠BEF,FN平分∠EFC,∴∠MEF=∠BEF,∠EFN=∠EFC,∴∠MEF=∠EFN,∴EM∥FN,∴∠M=∠N.
12.【解析】
解:猜想:如图①,过点P作PG∥l1,
∵l1∥l2,
∴l1∥l2∥PG,
∴∠APG=∠PAC=15°,∠BPG=∠PBD=40°,
∴∠APB=∠APG+∠BPG=∠PAC+∠PBD=15°+40°=55°,
∴∠APB的大小为55度,
故答案为:55;
探究:如图①,∠PAC=∠APB﹣∠PBD,理由如下:
∵l1∥l2∥PG,
∴∠APG=∠PAC,∠BPG=∠PBD,
∴∠APB=∠APG+∠BPG=∠PAC+∠PBD,
∴∠PAC=∠APB﹣∠PBD;
拓展:∠PAC=∠PBD﹣∠APB或∠PAC=∠APB+∠PBD,理由如下:
如图,当点P在射线CE上时,
过点P作PG∥l1,
∴l1∥l2∥PG,
∴∠APG=∠PAC,∠BPG=∠PBD,
∴∠PAC=∠APG=∠BPG﹣∠APB,
∴∠PAC=∠PBD﹣∠APB;
当点P在射线DF上时,
过点P作PG∥l1,
∴l1∥l2∥PG,
∴∠APG=∠PAC,∠BPG=∠PBD,
∴∠PAC=∠APG=∠APB+∠BPG,
∴∠PAC=∠APB+∠PBD,
综上所述:当点P在射线CE上或在射线DF上时,∠PAC=∠PBD﹣∠APB或∠PAC=∠APB+∠PBD.
1
一、选择题
1.下列说法:①两直线平行,同旁内角互补;②内错角相等,两直线平行;③同位角相等,两直线平行;④垂直于同一条直线的两条直线平行,其中是平行线的性质的是 ( )
A.① B.②和③ C.④ D.①和④
2.如图,若AD∥BC,则下列结论正确的是( )
A.∠1=∠3 B.∠2=∠4 C.∠1=∠2 D.∠2=∠3
3.如图,a∥b,∠ABD的平分线交直线a于点C,CE⊥直线c于点E,∠1=24°,则∠2的大小为( )
A.114° B.142° C.147° D.156°
4.如图所示,直线l1//l2,∠1=40°,∠2=75°,则∠3等于( )
A.55° B.30° C.65° D.70°
二、填空题
5.如图,在四边形ABCD中,若∠A+∠B=180°,则∠C+∠D=_______.
6.将两张矩形纸片如图所示摆放,使其中一张矩形纸片的一个顶点恰好落在另一张矩形纸片的一条边上,则∠1+∠2=________.
7.如图,把一把直尺放在含30度角的直角三角板上,量得∠1=56°,则∠2的度数是 .
8.如图,已知AD∥BC,BD 平分∠ABC,∠A=112°,且BD⊥CD,则∠ADC= .
三、解答题
9.如图,直线AB∥CD,BC平分∠ABD,∠1=70°,求∠2的度数.
10.如图,直线EF∥GH,点A在EF上,AC交GH于点B,若∠FAC=72°,∠ACD=58°,点D在GH上,求∠BDC的度数.
11.如图,已知 ∠BEF+∠EFD=180°,EM平分∠BEF,FN平分∠EFC,求证:∠M=∠N.
12.如图①,直线l1∥l2,直线EF和直线l1.l2分别交于C.D两点,点A.B分别在直线l1.l2上,点P在直线EF上,连结PA.PB.
猜想:如图①,若点P在线段CD上,∠PAC=15°,∠PBD=40°,则∠APB的大小为 度.
探究:如图①,若点P在线段CD上,直接写出∠PAC.∠APB.∠PBD之间的数量关系.
拓展:如图②,若点P在射线CE上或在射线DF上时,直接写出∠PAC.∠APB.∠PBD之间的数量关系.
参考答案
一、选择题
1. 【答案】A;
【解析】两直线平行角的关系.
2.【答案】A;
【解析】∵AD∥BC,
∴∠3=∠1,
故选:A.
3.【答案】C;
【解析】∵∠1=24°,CE⊥直线c于点E,
∴∠EAC=90°﹣∠1=90°﹣24°=66°,
∵a∥b,
∴∠EAC=∠ABD=66°,
∵∠ABD的平分线交直线a于点C,
∴∠CBD,
∴∠2=180°﹣∠CBD=180°﹣33°=147°,
故选:C.
4.【答案】C;
【解析】∠3=180°-40°-75°=65°.
二、填空题
5.【答案】180°;
【解析】由已知可得:AD∥BC,由平行的性质可得:∠D+∠C=180°.
【答案】90°;
7.【答案】116°;
【解析】∵把一把直尺放在含30度角的直角三角板上,
∴a∥b,
∴∠1=∠3=56°,
∴∠4=180°﹣∠3=180°﹣56°=124°,
∴∠5=360°﹣∠4﹣90°﹣30°=360°﹣124°﹣90°﹣30°=116°,
∴∠2=∠5=116°,
故答案为:116°.
8.【答案】124°;
【解析】解:∵AD∥BC,∠A=112°,
∴∠ABC=180°﹣∠A=68°,
∵BD 平分∠ABC,
∴∠CBD∠ABC=34°,
∵BD⊥CD,
∴∠C=90°﹣∠CBD=56°,
∴∠ADC=180°﹣∠C=124°.
故答案为:124°.
三、解答题
9.【解析】
解:∵AB∥CD,
∴∠ABC=∠1=70°,∠ABD+∠BDC=180°,
∵BC平分∠ABD,
∴∠ABD=2∠ABC=140°,
∴∠BDC=180°﹣∠ABD=40°,
∴∠2=∠BDC=40°.
10.【解析】
解:∵EF∥GH,∴∠ABD+∠FAC=180°,∴∠ABD=180°﹣72°=108°,∵∠ABD=∠ACD+∠BDC,∴∠BDC=∠ABD﹣∠ACD=108°﹣58°=50°.
11.【解析】
解:∵∠BEF+∠EFD=180°,∴AB∥CD,∴∠BEF=∠EFC.
∵EM平分∠BEF,FN平分∠EFC,∴∠MEF=∠BEF,∠EFN=∠EFC,∴∠MEF=∠EFN,∴EM∥FN,∴∠M=∠N.
12.【解析】
解:猜想:如图①,过点P作PG∥l1,
∵l1∥l2,
∴l1∥l2∥PG,
∴∠APG=∠PAC=15°,∠BPG=∠PBD=40°,
∴∠APB=∠APG+∠BPG=∠PAC+∠PBD=15°+40°=55°,
∴∠APB的大小为55度,
故答案为:55;
探究:如图①,∠PAC=∠APB﹣∠PBD,理由如下:
∵l1∥l2∥PG,
∴∠APG=∠PAC,∠BPG=∠PBD,
∴∠APB=∠APG+∠BPG=∠PAC+∠PBD,
∴∠PAC=∠APB﹣∠PBD;
拓展:∠PAC=∠PBD﹣∠APB或∠PAC=∠APB+∠PBD,理由如下:
如图,当点P在射线CE上时,
过点P作PG∥l1,
∴l1∥l2∥PG,
∴∠APG=∠PAC,∠BPG=∠PBD,
∴∠PAC=∠APG=∠BPG﹣∠APB,
∴∠PAC=∠PBD﹣∠APB;
当点P在射线DF上时,
过点P作PG∥l1,
∴l1∥l2∥PG,
∴∠APG=∠PAC,∠BPG=∠PBD,
∴∠PAC=∠APG=∠APB+∠BPG,
∴∠PAC=∠APB+∠PBD,
综上所述:当点P在射线CE上或在射线DF上时,∠PAC=∠PBD﹣∠APB或∠PAC=∠APB+∠PBD.
1
