5.6 二次函数的图像与一元二次方程课件
文档属性
| 名称 | 5.6 二次函数的图像与一元二次方程课件 |

|
|
| 格式 | zip | ||
| 文件大小 | 629.8KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 青岛版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2014-12-25 00:00:00 | ||
图片预览





文档简介
课件15张PPT。§5.6 二次函数的图象与一元二次方程第5章 对函数的再探索巨野县龙堌镇第一中学 张常玉学习目标1、经历探究二次函数y=ax2+bx+c和一元二次方程ax2+bx+c=0关系的过程,掌握二次函数和一元二次方程的关系
2、能利用二次函数图像讨论一元二次方程的实数根,反过来利用一元二次方程的实数根讨论二次函数图像与x轴交点
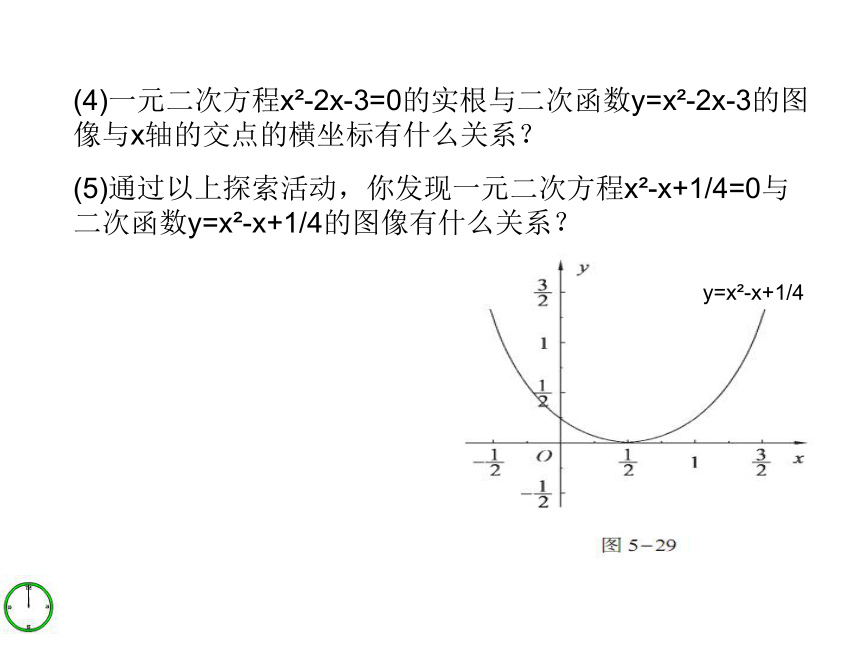
3、进一步体会数形结合思想和函数与方程思想的综合运用,感知数学美问题:比较二次函数的表达式y=x2-2x-3与一元二次方程x2-2x-3=0 ,你能说出二者之间有什么关系吗?(5)通过以上探索活动,你发现一元二次方程x2-x+1/4=0与二次函数y=x2-x+1/4的图像有什么关系?(4)一元二次方程x2-2x-3=0的实根与二次函数y=x2-2x-3的图像与x轴的交点的横坐标有什么关系?y=x2-x+1/4(6)一般的,如果一元二次方程ax2+bx+c=0有实根,那么该方程的实根与二次函数y=ax2+bx+c的图像与x轴的公共点的横坐标有什么关系?你知道吗?我总结我快乐如果一元二次方程ax2+bx+c=0有实根,那么二次函数y=ax2+bx+c的图像与x轴有公共点,且公共点的横坐标是这个一元二次方程的实数根;反之,如果二次函数y=ax2+bx+c的图像与x轴有公共点,那么公共点的横坐标就是一元二次方程ax2+bx+c=0的实数根。学以致用挑战自我已知抛物线y=ax2+bx+c ,当a、b、c满足什么条件时,
(1)抛物线与x轴有两个公共点?
(2)抛物线与x轴只有一个公共点?
(3)抛物线与x轴没有公共点?
b2-4ac <0b2-4ac>0b2-4ac=0a ≠0且a ≠0且a ≠0且1、求二次函数y=2x2-4x-1的图像与x轴的公共点的坐标2、利用二次函数的图像求一元二次方程x2-8x+6=0的近似解?(精确到0.1)3、判断下列二次函数的图像与x轴是否有公共点,如果有,有几个公共点?
(1) y=-1/4x2+4x-1
(2) y=x2+x+2
(3) y=x2-3x-4我要成功小 结二次函数y=ax2+bx+c与一元二次方程ax2+bx+c=0关系:
△=b2-4ac≥0 一元二次方程ax2+bx+c=0有实数根 抛物线y=ax2+bx+c与x轴有两个交点
△=b2-4ac <0 一元二次方程ax2+bx+c=0无实数根 抛物线y=ax2+bx+c与x轴没有交点
作业题
必做题:习题5.6 4题、5题
选做题:习题5.6 6题
同学们,
再见!
2、能利用二次函数图像讨论一元二次方程的实数根,反过来利用一元二次方程的实数根讨论二次函数图像与x轴交点
3、进一步体会数形结合思想和函数与方程思想的综合运用,感知数学美问题:比较二次函数的表达式y=x2-2x-3与一元二次方程x2-2x-3=0 ,你能说出二者之间有什么关系吗?(5)通过以上探索活动,你发现一元二次方程x2-x+1/4=0与二次函数y=x2-x+1/4的图像有什么关系?(4)一元二次方程x2-2x-3=0的实根与二次函数y=x2-2x-3的图像与x轴的交点的横坐标有什么关系?y=x2-x+1/4(6)一般的,如果一元二次方程ax2+bx+c=0有实根,那么该方程的实根与二次函数y=ax2+bx+c的图像与x轴的公共点的横坐标有什么关系?你知道吗?我总结我快乐如果一元二次方程ax2+bx+c=0有实根,那么二次函数y=ax2+bx+c的图像与x轴有公共点,且公共点的横坐标是这个一元二次方程的实数根;反之,如果二次函数y=ax2+bx+c的图像与x轴有公共点,那么公共点的横坐标就是一元二次方程ax2+bx+c=0的实数根。学以致用挑战自我已知抛物线y=ax2+bx+c ,当a、b、c满足什么条件时,
(1)抛物线与x轴有两个公共点?
(2)抛物线与x轴只有一个公共点?
(3)抛物线与x轴没有公共点?
b2-4ac <0b2-4ac>0b2-4ac=0a ≠0且a ≠0且a ≠0且1、求二次函数y=2x2-4x-1的图像与x轴的公共点的坐标2、利用二次函数的图像求一元二次方程x2-8x+6=0的近似解?(精确到0.1)3、判断下列二次函数的图像与x轴是否有公共点,如果有,有几个公共点?
(1) y=-1/4x2+4x-1
(2) y=x2+x+2
(3) y=x2-3x-4我要成功小 结二次函数y=ax2+bx+c与一元二次方程ax2+bx+c=0关系:
△=b2-4ac≥0 一元二次方程ax2+bx+c=0有实数根 抛物线y=ax2+bx+c与x轴有两个交点
△=b2-4ac <0 一元二次方程ax2+bx+c=0无实数根 抛物线y=ax2+bx+c与x轴没有交点
作业题
必做题:习题5.6 4题、5题
选做题:习题5.6 6题
同学们,
再见!
