2023-2024学年高中化学苏教版(2019)选择性必修二 3.1.2金属键 金属晶体 课件(共22张PPT)
文档属性
| 名称 | 2023-2024学年高中化学苏教版(2019)选择性必修二 3.1.2金属键 金属晶体 课件(共22张PPT) |  | |
| 格式 | pptx | ||
| 文件大小 | 10.4MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 苏教版(2019) | ||
| 科目 | 化学 | ||
| 更新时间 | 2023-09-12 14:41:03 | ||
图片预览






文档简介
(共22张PPT)
3.1金属键 金属晶体
第二课时
自然界中许多固态物质都是晶体,它们有规则的几何外形,如晶莹的雪花、玲珑剔透的石英、棱角分明的食盐固体和许多矿石。通常条件下,大多数金属单质也是晶体。
1.定义:金属原子之间通过金属键相互结合形成的晶体。
2.组成粒子:金属阳离子和自由电子。
3.微粒间的作用力:金属键
一、金属晶体
铜的晶体结构模型
注意:
②在金属晶体中,不存在单个分子或原子,金属单质或合金(晶体锗、灰锡除外)属于金属晶体。
①在金属晶体中有阳离子,但没有阴离子,所以,晶体中有阳离子不一定有阴离子,若有阴离子,则一定有阳离子。
③金属晶体在受外力作用下,各层之间发生相对滑动,但金属键并没有被破坏。
金属晶体熔、沸点高低的比较
金属阳离子半径越小,所带电荷越多,则金属键越强,金属的熔、沸点就越高,一般存在以下规律:
(1)同周期金属单质(如Na、Mg、Al),从左到右熔、沸点逐渐升高。
(2)同主族金属单质(如碱金属),从上到下熔、沸点逐渐降低。
(3)合金的熔、沸点比其各成分金属的熔、沸点低。
(4)金属晶体熔点差别很大,如汞在常温下为液体,熔点很低(-38.9 ℃),而铁等金属熔点很高(1535℃)。
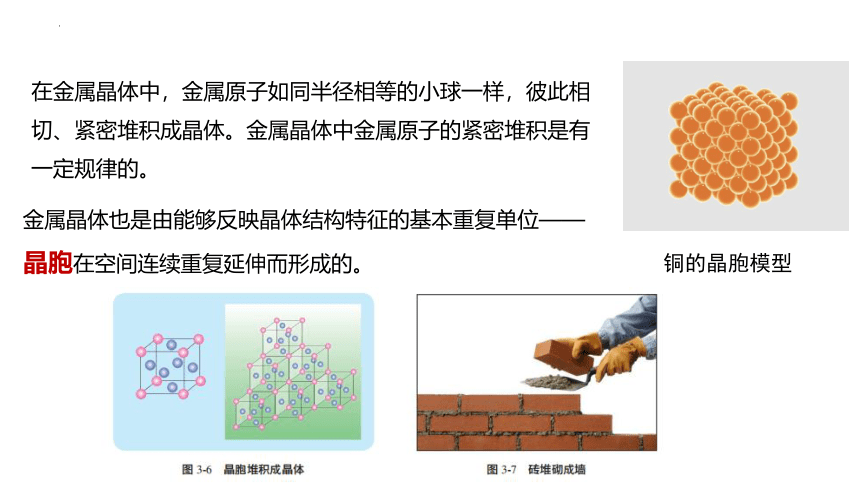
在金属晶体中,金属原子如同半径相等的小球一样,彼此相切、紧密堆积成晶体。金属晶体中金属原子的紧密堆积是有一定规律的。
铜的晶胞模型
金属晶体也是由能够反映晶体结构特征的基本重复单位——晶胞在空间连续重复延伸而形成的。
二、金属晶体常见堆积方式
如果金属原子在平面上(二维空间)紧密放置,可有两种排列方式
非密置层
密置层
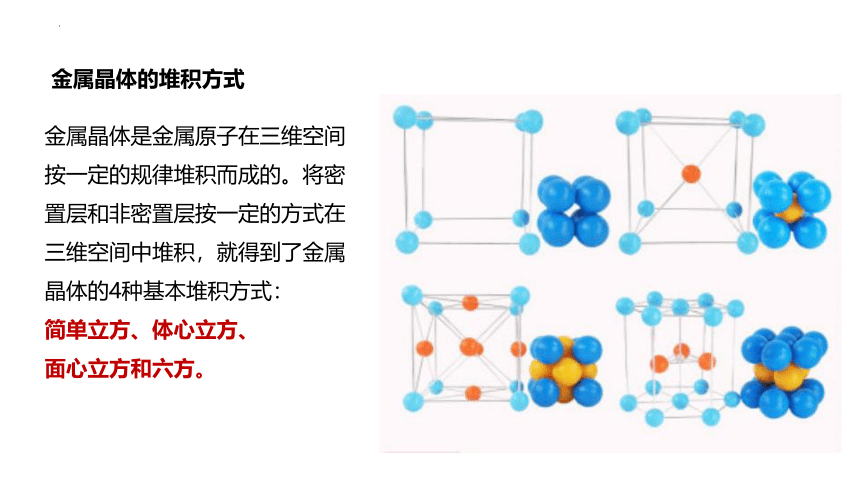
金属晶体是金属原子在三维空间按一定的规律堆积而成的。将密置层和非密置层按一定的方式在三维空间中堆积,就得到了金属晶体的4种基本堆积方式:
简单立方、体心立方、
面心立方和六方。
金属晶体的堆积方式
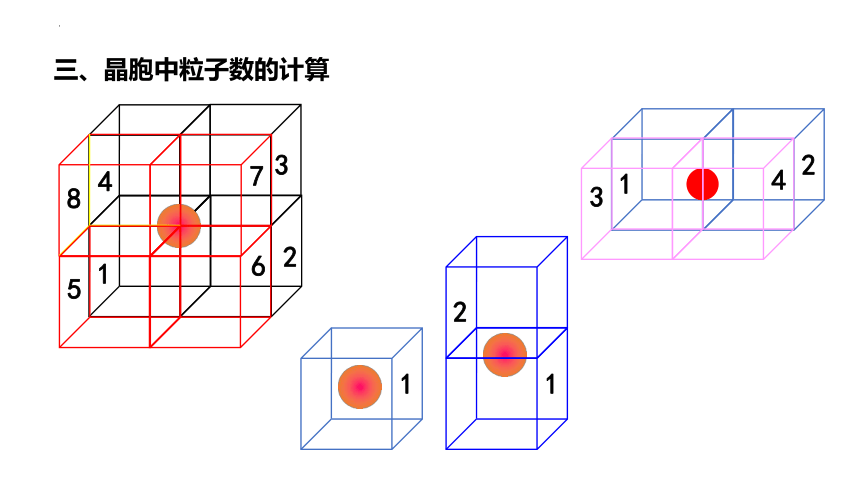
三、晶胞中粒子数的计算
1
2
4
3
7
6
8
5
1
2
2
1
3
4
1
三、晶胞中粒子数的计算
处在立方体顶点的金属原子为8个晶胞共享,该原子的 属于该晶胞。
三、晶胞中粒子数的计算
处于立方体棱上的金属原子为4个晶胞共享,该原子的 属于该晶胞。
三、晶胞中粒子数的计算
处于立方体面上的金属原子为2个晶胞共享,该原子的 属于该晶胞。
三、晶胞中粒子数的计算
处于立方体体心的金属原子完全属于该晶胞。
1、简单立方堆积
只有金属钋(Po)采用这种堆积方式
该晶胞中含有8个位于顶点的金属原子,晶胞中的金属原子数为
8× =1
三、晶胞中粒子数的计算
简单立方晶胞切面示意图
2、体心立方堆积
钠、钾、铬、钼、钨等
该晶胞中含有8个位于顶点和1个位于体心的金属原子,
晶胞中的金属原子数为:
8× +1=2
体心立方晶胞切面示意图
三、晶胞中粒子数的计算
3、面心立方堆积
金、银、铜、铅等
该晶胞中含有8个位于顶点和6个位于面心的金属原子,
晶胞中的金属原子数为:
三、晶胞中粒子数的计算
8× +6× =4
面心立方晶胞切面示意图
4、六方堆积
镁、锌、钛等
三、晶胞中粒子数的计算
六方晶胞切面示意图
思考:立方晶胞中的金属原子数如何计算?
六棱柱
体心(内部)
1
面心
1/2
棱边
水平1/4 竖1/3
顶点
1/6
4、六方堆积
三、晶胞中粒子数的计算
该晶胞中含有12个位于顶点、2个位于面心和3个位于内部的金属原子,
晶胞中的金属原子数为:
12× +2× +3=6
课堂小结
一、金属晶体
二、金属晶体常见堆积方式
三、晶胞中粒子数的计算
三维:简单立方、体心立方、 面心立方和六方
二维:非密置层、密置层
定义、注意事项及特征
均摊法计算的应用
课堂练习
D
1. 下列叙述正确的是( )
A. 任何晶体中,若含有阳离子,就一定含有阴离子
B. 金属晶体的形成是因为晶体中存在金属离子间的相互作用
C. 价电子越多的金属原子的金属性越强
D. 含有金属元素的离子不一定是阳离子
1:4:2
2、金属晶体中金属原子有三种常见的堆积方式:简单立方堆积、面心立方堆积和体心立方堆积,图a、b、c分别代表这三种晶胞的结构。请回答下列问题:
(1)a、b、c三种晶胞内金属原子数目之比为 。
(2)三种堆积方式的实质是金属阳离子的堆积方式,那么自由电子有无确切的堆积方式? (填“有”或“无”)。
(3)影响金属晶体熔点的主要因素是 。
无
金属键的强弱
3.1金属键 金属晶体
第二课时
自然界中许多固态物质都是晶体,它们有规则的几何外形,如晶莹的雪花、玲珑剔透的石英、棱角分明的食盐固体和许多矿石。通常条件下,大多数金属单质也是晶体。
1.定义:金属原子之间通过金属键相互结合形成的晶体。
2.组成粒子:金属阳离子和自由电子。
3.微粒间的作用力:金属键
一、金属晶体
铜的晶体结构模型
注意:
②在金属晶体中,不存在单个分子或原子,金属单质或合金(晶体锗、灰锡除外)属于金属晶体。
①在金属晶体中有阳离子,但没有阴离子,所以,晶体中有阳离子不一定有阴离子,若有阴离子,则一定有阳离子。
③金属晶体在受外力作用下,各层之间发生相对滑动,但金属键并没有被破坏。
金属晶体熔、沸点高低的比较
金属阳离子半径越小,所带电荷越多,则金属键越强,金属的熔、沸点就越高,一般存在以下规律:
(1)同周期金属单质(如Na、Mg、Al),从左到右熔、沸点逐渐升高。
(2)同主族金属单质(如碱金属),从上到下熔、沸点逐渐降低。
(3)合金的熔、沸点比其各成分金属的熔、沸点低。
(4)金属晶体熔点差别很大,如汞在常温下为液体,熔点很低(-38.9 ℃),而铁等金属熔点很高(1535℃)。
在金属晶体中,金属原子如同半径相等的小球一样,彼此相切、紧密堆积成晶体。金属晶体中金属原子的紧密堆积是有一定规律的。
铜的晶胞模型
金属晶体也是由能够反映晶体结构特征的基本重复单位——晶胞在空间连续重复延伸而形成的。
二、金属晶体常见堆积方式
如果金属原子在平面上(二维空间)紧密放置,可有两种排列方式
非密置层
密置层
金属晶体是金属原子在三维空间按一定的规律堆积而成的。将密置层和非密置层按一定的方式在三维空间中堆积,就得到了金属晶体的4种基本堆积方式:
简单立方、体心立方、
面心立方和六方。
金属晶体的堆积方式
三、晶胞中粒子数的计算
1
2
4
3
7
6
8
5
1
2
2
1
3
4
1
三、晶胞中粒子数的计算
处在立方体顶点的金属原子为8个晶胞共享,该原子的 属于该晶胞。
三、晶胞中粒子数的计算
处于立方体棱上的金属原子为4个晶胞共享,该原子的 属于该晶胞。
三、晶胞中粒子数的计算
处于立方体面上的金属原子为2个晶胞共享,该原子的 属于该晶胞。
三、晶胞中粒子数的计算
处于立方体体心的金属原子完全属于该晶胞。
1、简单立方堆积
只有金属钋(Po)采用这种堆积方式
该晶胞中含有8个位于顶点的金属原子,晶胞中的金属原子数为
8× =1
三、晶胞中粒子数的计算
简单立方晶胞切面示意图
2、体心立方堆积
钠、钾、铬、钼、钨等
该晶胞中含有8个位于顶点和1个位于体心的金属原子,
晶胞中的金属原子数为:
8× +1=2
体心立方晶胞切面示意图
三、晶胞中粒子数的计算
3、面心立方堆积
金、银、铜、铅等
该晶胞中含有8个位于顶点和6个位于面心的金属原子,
晶胞中的金属原子数为:
三、晶胞中粒子数的计算
8× +6× =4
面心立方晶胞切面示意图
4、六方堆积
镁、锌、钛等
三、晶胞中粒子数的计算
六方晶胞切面示意图
思考:立方晶胞中的金属原子数如何计算?
六棱柱
体心(内部)
1
面心
1/2
棱边
水平1/4 竖1/3
顶点
1/6
4、六方堆积
三、晶胞中粒子数的计算
该晶胞中含有12个位于顶点、2个位于面心和3个位于内部的金属原子,
晶胞中的金属原子数为:
12× +2× +3=6
课堂小结
一、金属晶体
二、金属晶体常见堆积方式
三、晶胞中粒子数的计算
三维:简单立方、体心立方、 面心立方和六方
二维:非密置层、密置层
定义、注意事项及特征
均摊法计算的应用
课堂练习
D
1. 下列叙述正确的是( )
A. 任何晶体中,若含有阳离子,就一定含有阴离子
B. 金属晶体的形成是因为晶体中存在金属离子间的相互作用
C. 价电子越多的金属原子的金属性越强
D. 含有金属元素的离子不一定是阳离子
1:4:2
2、金属晶体中金属原子有三种常见的堆积方式:简单立方堆积、面心立方堆积和体心立方堆积,图a、b、c分别代表这三种晶胞的结构。请回答下列问题:
(1)a、b、c三种晶胞内金属原子数目之比为 。
(2)三种堆积方式的实质是金属阳离子的堆积方式,那么自由电子有无确切的堆积方式? (填“有”或“无”)。
(3)影响金属晶体熔点的主要因素是 。
无
金属键的强弱
