2023-2024学年高中数学苏教版(2019)必修第一册 3-2-1基本不等式的证明 课件(20张)
文档属性
| 名称 | 2023-2024学年高中数学苏教版(2019)必修第一册 3-2-1基本不等式的证明 课件(20张) |

|
|
| 格式 | pptx | ||
| 文件大小 | 384.3KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 苏教版(2019) | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-09-12 11:23:46 | ||
图片预览








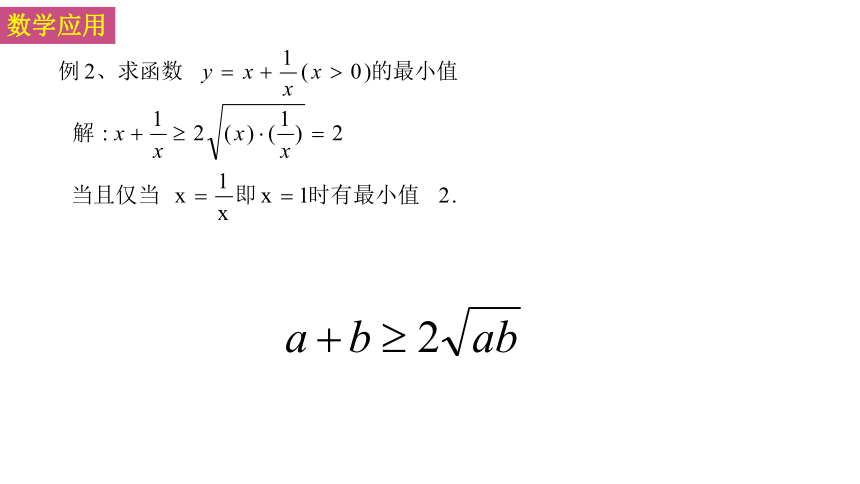
文档简介
(共20张PPT)
3.2.1基本不等式的证明
学习目标
1.了解两个正数的算术平均数与几何平均数的概念,能推导并掌握基本不等式;
2.理解基本不等式的几何意义,能运用基本不等式进行简单证明
情景引入
问题1.你能用这个图得出基本不等式的几何解释吗
A
B
C
D
E
a
b
O
如图, AB是圆的直径, O为圆心,点C是AB上一点, AC=a, BC=b. 过点C作垂直于AB的弦DE,连接AD、BD、OD.
②如何用a, b表示CD CD=______
①如何用a, b表示OD OD=______
③OD与CD的大小关系怎样 OD_____CD
≥
数学建构
则
算术平均数
几何平均数
两个正数的算术平均数不小于它们的几何平均数.
符号语言
文字语言
数学建构
如果 ,
称为基本不等式.
当且仅当 时,取等号.
则
如何证明这个基本不等式?
合作探究
证法2:
分析法——执果索因
证法3:
综合法——由因导果
证法1:
比较法(作差法)
数学应用
例1.已知ab>0,求证: ,并推导出式中等号成立的条件。
证明:因为ab>0,所以 ,根据均值不等式得
即
当且仅当 时,即a2=b2时式中等号成立,
因为ab>0,即a,b同号,所以式中等号成立的条件是a=b.
数学应用
变. 已知:a,b,c均为正数, 求证:
证明:
所以,原不等式成立
当且仅当a=b=c时,取等号.
数学应用
变、命题:“若ab>0,则 .” 是真命题,下列说法正确的是( )
C
数学应用
数学应用
数学应用
解: ∵00.
∴y=x(1-x)
≤ [ ]2
x+(1-x)
2
1
4
= .
当且仅当 时, 取“=”号.
x=(1-x),
即 x=
1
2
∴当 x = 时, 函数 y=x(1-x) 的最大值是 .
1
2
1
4
例3. 若 0数学应用
配凑系数
分析: x+(1-2x) 不是 常数.
2
=1为
解: ∵00.
1
2
∴y=x(1-2x)= 2x (1-2x)
1
2
≤ [ ]2
2x+(1-2x)
2
1
2
1
8
= .
当且仅当 时, 取“=”号.
2x=(1-2x),
即 x=
1
4
∴当 x = 时, 函数 y=x(1-2x) 的最大值是 .
1
4
1
8
变. 若 01
2
数学建构
(1)如果a,b>0,且ab=P(定值),那么
a+b有最____值______(当且仅当_____时取“=”).
(2)如果a,b>0,且a+b=S (定值),那么
ab有最____值______(当且仅当______时取“=”).
利用基本不等式求最值问题:
小
大
a=b
a=b
一正二定三相等
“积定和最小”
“和定积最大”
典型例题
典型例题
“1”的常值代换
课堂小结
课堂达标
1.函数
的值域是___________
2.若
(用不等号连接)
___
3.已知
,函数
的最大值是
_____
4.若
,则函数
的最小值是
_____
5.若
是正实数,则
的最小值是
_____
课堂达标
7、已知
,且
解:(1)由
得
又
,则
,得
当且仅当
时,等号成立。
求(1)
的最小值;(2)
的最小值。
xy
课堂达标
7、已知
,且
求(1)
的最小值;(2)
的最小值。
xy
(2)由
,得
则
当且仅当
取到等号。
谢谢
3.2.1基本不等式的证明
学习目标
1.了解两个正数的算术平均数与几何平均数的概念,能推导并掌握基本不等式;
2.理解基本不等式的几何意义,能运用基本不等式进行简单证明
情景引入
问题1.你能用这个图得出基本不等式的几何解释吗
A
B
C
D
E
a
b
O
如图, AB是圆的直径, O为圆心,点C是AB上一点, AC=a, BC=b. 过点C作垂直于AB的弦DE,连接AD、BD、OD.
②如何用a, b表示CD CD=______
①如何用a, b表示OD OD=______
③OD与CD的大小关系怎样 OD_____CD
≥
数学建构
则
算术平均数
几何平均数
两个正数的算术平均数不小于它们的几何平均数.
符号语言
文字语言
数学建构
如果 ,
称为基本不等式.
当且仅当 时,取等号.
则
如何证明这个基本不等式?
合作探究
证法2:
分析法——执果索因
证法3:
综合法——由因导果
证法1:
比较法(作差法)
数学应用
例1.已知ab>0,求证: ,并推导出式中等号成立的条件。
证明:因为ab>0,所以 ,根据均值不等式得
即
当且仅当 时,即a2=b2时式中等号成立,
因为ab>0,即a,b同号,所以式中等号成立的条件是a=b.
数学应用
变. 已知:a,b,c均为正数, 求证:
证明:
所以,原不等式成立
当且仅当a=b=c时,取等号.
数学应用
变、命题:“若ab>0,则 .” 是真命题,下列说法正确的是( )
C
数学应用
数学应用
数学应用
解: ∵0
∴y=x(1-x)
≤ [ ]2
x+(1-x)
2
1
4
= .
当且仅当 时, 取“=”号.
x=(1-x),
即 x=
1
2
∴当 x = 时, 函数 y=x(1-x) 的最大值是 .
1
2
1
4
例3. 若 0
配凑系数
分析: x+(1-2x) 不是 常数.
2
=1为
解: ∵0
1
2
∴y=x(1-2x)= 2x (1-2x)
1
2
≤ [ ]2
2x+(1-2x)
2
1
2
1
8
= .
当且仅当 时, 取“=”号.
2x=(1-2x),
即 x=
1
4
∴当 x = 时, 函数 y=x(1-2x) 的最大值是 .
1
4
1
8
变. 若 0
2
数学建构
(1)如果a,b>0,且ab=P(定值),那么
a+b有最____值______(当且仅当_____时取“=”).
(2)如果a,b>0,且a+b=S (定值),那么
ab有最____值______(当且仅当______时取“=”).
利用基本不等式求最值问题:
小
大
a=b
a=b
一正二定三相等
“积定和最小”
“和定积最大”
典型例题
典型例题
“1”的常值代换
课堂小结
课堂达标
1.函数
的值域是___________
2.若
(用不等号连接)
___
3.已知
,函数
的最大值是
_____
4.若
,则函数
的最小值是
_____
5.若
是正实数,则
的最小值是
_____
课堂达标
7、已知
,且
解:(1)由
得
又
,则
,得
当且仅当
时,等号成立。
求(1)
的最小值;(2)
的最小值。
xy
课堂达标
7、已知
,且
求(1)
的最小值;(2)
的最小值。
xy
(2)由
,得
则
当且仅当
取到等号。
谢谢
同课章节目录
- 第1章 集合
- 1.1 集合的概念与表示
- 1.2 子集、全集、补集
- 1.3 交集、并集
- 第2章 常用逻辑用语
- 2.1 命题、定理、定义
- 2.2 充分条件、必要条件、冲要条件
- 2.3 全称量词命题与存在量词命题
- 第3章 不等式
- 3.1 不等式的基本性质
- 3.2 基本不等式
- 3.3 从函数观点看一元二次方程和一元二次不等式
- 第4章 指数与对数
- 4.1 指数
- 4.2 对数
- 第5章 函数概念与性质
- 5.1 函数的概念和图象
- 5.2 函数的表示方法
- 5.3 函数的单调性
- 5.4 函数的奇偶性
- 第6章 幂函数、指数函数和对数函数
- 6.1 幂函数
- 6.2 指数函数
- 6.3 对数函数
- 第7章 三角函数
- 7.1 角与弧度
- 7.2 三角函数概念
- 7.3 三角函数的图象和性质
- 7.4 三角函数应用
- 第8章 函数应用
- 8.1 二分法与求方程近似解
- 8.2 函数与数学模型
