2023-2024学年高中数学苏教版(2019)必修第一册 3-3-1从函数观点看一元二次方程 课件(16张)
文档属性
| 名称 | 2023-2024学年高中数学苏教版(2019)必修第一册 3-3-1从函数观点看一元二次方程 课件(16张) |

|
|
| 格式 | pptx | ||
| 文件大小 | 431.8KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 苏教版(2019) | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-09-12 11:24:19 | ||
图片预览




文档简介
(共16张PPT)
3.3.1从函数观点看一元二次方程
学习目标
1.理解函数零点的概念.
2.能根据“两个二次”之间的关系研究函数的零点.
3.通过以一元二次方程研究函数的零点的学习,培养数学抽象和数学运算素养.
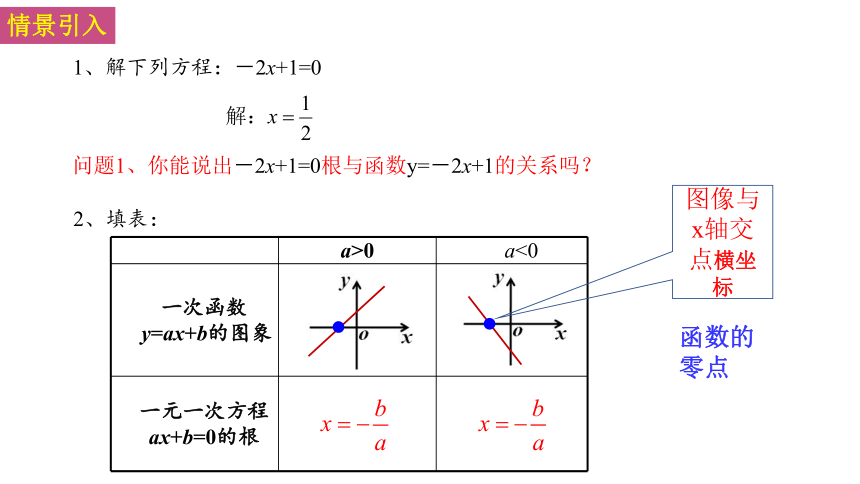
情景引入
1、解下列方程:-2x+1=0
a>0 a<0
一次函数 y=ax+b的图象
一元一次方程 ax+b=0的根
2、填表:
问题1、你能说出-2x+1=0根与函数y=-2x+1的关系吗?
图像与x轴交点横坐标
函数的零点
情景引入
横坐标
自变量x
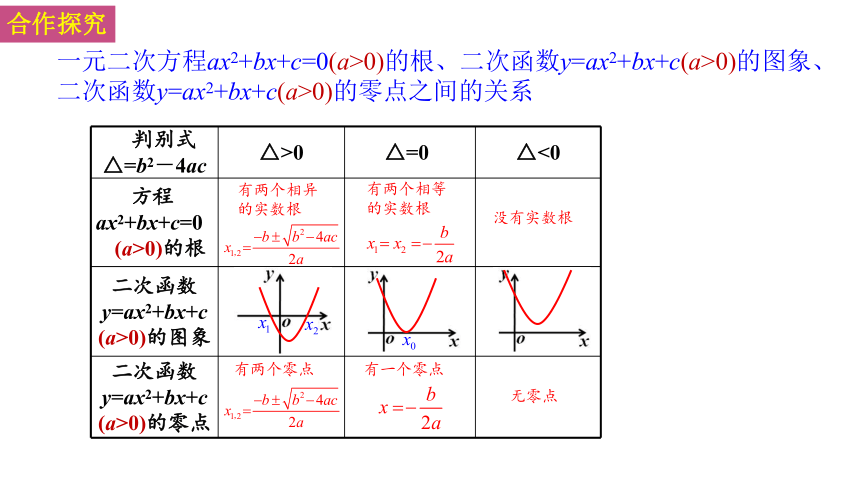
合作探究
一元二次方程ax2+bx+c=0(a>0)的根、二次函数y=ax2+bx+c(a>0)的图象、二次函数y=ax2+bx+c(a>0)的零点之间的关系
判别式△=b2-4ac △>0 △=0 △<0
方程 ax2+bx+c=0 (a>0)的根
二次函数y=ax2+bx+c (a>0)的图象
二次函数y=ax2+bx+c (a>0)的零点
有两个相异
的实数根
有两个相等
的实数根
没有实数根
有两个零点
有一个零点
无零点
合作探究
请填写下表:
判别式△=b2-4ac △>0 △=0 △<0
方程 ax2+bx+c=0 (a<0)的根
二次函数y=ax2+bx+c (a<0)的图象
二次函数y=ax2+bx+c (a<0)的零点
有两个相异
的实数根
有两个相等
的实数根
没有实数根
有两个零点
有一个零点
无零点
数学应用
数学建构
方法一、直接解出相应方程的根
函数零点 研究方法
数学应用
数学应用
数学建构
方法一、直接解出相应方程的根
函数零点 研究方法
方法二、韦达定理
数学应用
课堂小结
方法一、直接解出相应方程的根
函数零点 研究方法
方法三、利用函数的图像的特征
开口
判别式
对称轴
端点值
方法二、韦达定理
课堂达标
答案:B
课堂达标
课堂达标
谢谢
3.3.1从函数观点看一元二次方程
学习目标
1.理解函数零点的概念.
2.能根据“两个二次”之间的关系研究函数的零点.
3.通过以一元二次方程研究函数的零点的学习,培养数学抽象和数学运算素养.
情景引入
1、解下列方程:-2x+1=0
a>0 a<0
一次函数 y=ax+b的图象
一元一次方程 ax+b=0的根
2、填表:
问题1、你能说出-2x+1=0根与函数y=-2x+1的关系吗?
图像与x轴交点横坐标
函数的零点
情景引入
横坐标
自变量x
合作探究
一元二次方程ax2+bx+c=0(a>0)的根、二次函数y=ax2+bx+c(a>0)的图象、二次函数y=ax2+bx+c(a>0)的零点之间的关系
判别式△=b2-4ac △>0 △=0 △<0
方程 ax2+bx+c=0 (a>0)的根
二次函数y=ax2+bx+c (a>0)的图象
二次函数y=ax2+bx+c (a>0)的零点
有两个相异
的实数根
有两个相等
的实数根
没有实数根
有两个零点
有一个零点
无零点
合作探究
请填写下表:
判别式△=b2-4ac △>0 △=0 △<0
方程 ax2+bx+c=0 (a<0)的根
二次函数y=ax2+bx+c (a<0)的图象
二次函数y=ax2+bx+c (a<0)的零点
有两个相异
的实数根
有两个相等
的实数根
没有实数根
有两个零点
有一个零点
无零点
数学应用
数学建构
方法一、直接解出相应方程的根
函数零点 研究方法
数学应用
数学应用
数学建构
方法一、直接解出相应方程的根
函数零点 研究方法
方法二、韦达定理
数学应用
课堂小结
方法一、直接解出相应方程的根
函数零点 研究方法
方法三、利用函数的图像的特征
开口
判别式
对称轴
端点值
方法二、韦达定理
课堂达标
答案:B
课堂达标
课堂达标
谢谢
同课章节目录
- 第1章 集合
- 1.1 集合的概念与表示
- 1.2 子集、全集、补集
- 1.3 交集、并集
- 第2章 常用逻辑用语
- 2.1 命题、定理、定义
- 2.2 充分条件、必要条件、冲要条件
- 2.3 全称量词命题与存在量词命题
- 第3章 不等式
- 3.1 不等式的基本性质
- 3.2 基本不等式
- 3.3 从函数观点看一元二次方程和一元二次不等式
- 第4章 指数与对数
- 4.1 指数
- 4.2 对数
- 第5章 函数概念与性质
- 5.1 函数的概念和图象
- 5.2 函数的表示方法
- 5.3 函数的单调性
- 5.4 函数的奇偶性
- 第6章 幂函数、指数函数和对数函数
- 6.1 幂函数
- 6.2 指数函数
- 6.3 对数函数
- 第7章 三角函数
- 7.1 角与弧度
- 7.2 三角函数概念
- 7.3 三角函数的图象和性质
- 7.4 三角函数应用
- 第8章 函数应用
- 8.1 二分法与求方程近似解
- 8.2 函数与数学模型
