2023-2024学年高中数学苏教版(2019)必修第一册 4-2-1对数的概念 课件(20张)
文档属性
| 名称 | 2023-2024学年高中数学苏教版(2019)必修第一册 4-2-1对数的概念 课件(20张) |

|
|
| 格式 | pptx | ||
| 文件大小 | 458.6KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 苏教版(2019) | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-09-12 11:26:20 | ||
图片预览







文档简介
(共20张PPT)
4.2.1对数的概念
学习目标
情景引入
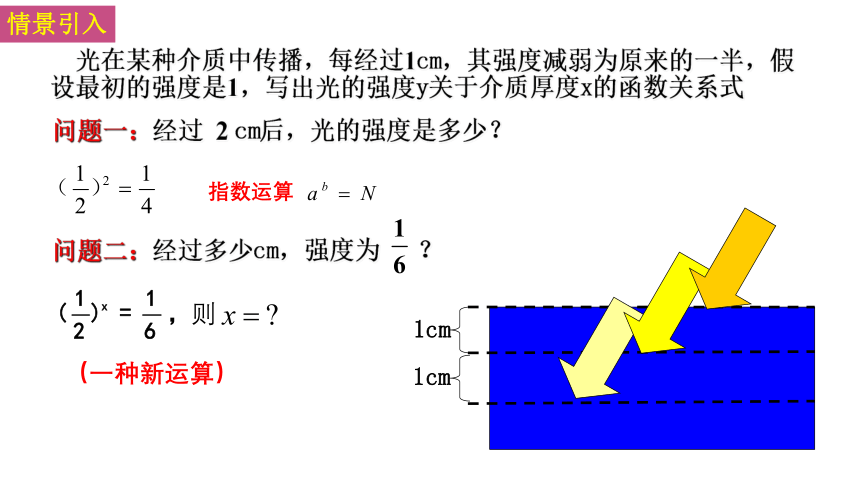
光在某种介质中传播,每经过1cm,其强度减弱为原来的一半,假设最初的强度是1,写出光的强度y关于介质厚度x的函数关系式
问题一:经过 2 cm后,光的强度是多少?
问题二:经过多少cm,强度为 ?
1cm
1cm
指数运算
,则
(一种新运算)
复习引入
观察数的运算的发展,思考问题:
(1)已知a+x=N,求 x
引入减法
x=N-a
(2)已知ax=N , 求 x
引入除法
(3)已知 ,求 x
引入开方
(4)已知 ,求 x
引入什么?
对数!
概念形成
对数的定义:
一般地,如果 ,那么数x叫做以a为底N的对数(logarithm),记作 .
其中a叫做对数的底数,N叫做真数,读作:以a为底N的对数.
表示一种运算
概念巩固
利用下表解下列方程
合作探究
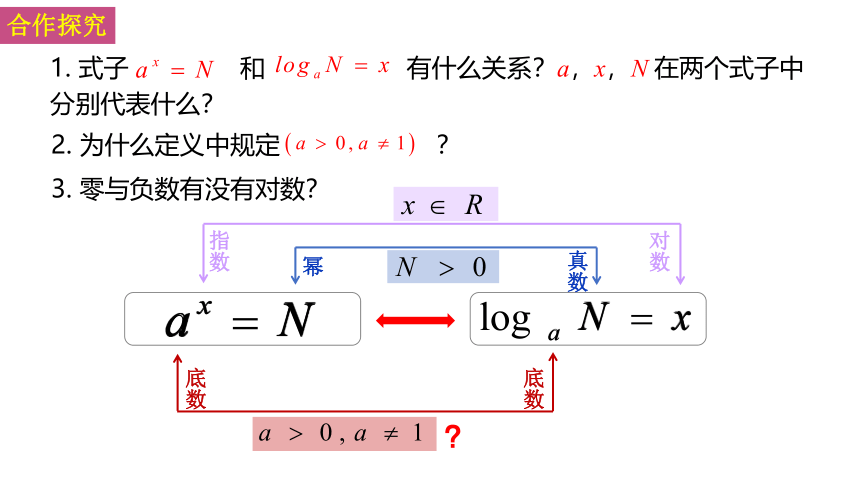
1. 式子 和 有什么关系?a,x,N 在两个式子中分别代表什么?
3. 零与负数有没有对数?
2. 为什么定义中规定 ?
合作探究
1. 式子 和 有什么关系?a,x,N 在两个式子中分别代表什么?
3. 零与负数有没有对数?
2. 为什么定义中规定 ?
底数
底数
指数
对数
幂
真数
?
数学应用
1、写出所有对数,其中底数和真数A 的元素;
集合A
-1,0,1,2,e,4,10
)
数学应用
1、写出所有对数,其中底数和真数A 的元素;
集合A
-1,0,1,2,e,4,10
=1
=1
=1
=1
=0
=0
=0
=0
=0.5
=2
计算器
2、求出所写对数的值或者它表示什么;
课堂小结
常用对数
自然对数
)
数学应用
1、写出所有对数,其中底数和真数A 的元素;
集合A
-1,0,1,2,e,4,10
=1
=1
=1
=1
=0
=0
=0
=0
=0.5
=2
计算器
2、求出所写对数的值或者它表示什么;
计算器
计算器
计算器
计算器
计算器
转化为常用对数
数学应用
1、写出所有对数,其中底数和真数A 的元素;
集合A
-1,0,1,2,e,4,10
=1
=1
=1
=1
=0
=0
=0
=0
=0.5
=2
计算器
2、求出所写对数的值或者它表示什么;
计算器
计算器
计算器
计算器
计算器
3、对数 , 有什么特点?
1 的对数等于0 (loga1=0).
底的对数等于1 (logaa=1).
数学应用
例1. 求下列各式中 x 的值:
(1) (2) logx8=6; (3) lg100=x; (4) -lne2=x.
解:
(1)
由 得
(2)
由 logx8=6 得
x6=8,
(3)
(4)
由 lg100=x 得
10x=100,
∴ x=2.
由 -lne2=x 得
e-x=e2,
lne2= -x,
化成指数式得
则 x= -2.
另解:x=lg100
=lg102
=2
另解:x=-lne2
=-2
课堂小结
解题总结:
1、指数式与对数式的互化
2、真数幂化
数学应用
例2. 求下列各式的值:
(1) log525; (2) (3) lg1000; (4) lg0.001.
解:
(1)
设 log525=x,
则 5x=25,
即得 x=2,
∴ log525 =2.
(2)
设
则
即得 x= -4,
(3)
设 lg1000=x,
则 10x=1000,
即得 x=3,
∴ lg1000 =3.
(4)
设 lg0.001=x,
则 10x=0.001,
即得 x= -3,
∴ lg0.001 = -3.
另解: log525
=log552
=2
合作探究
P83 T7、已知
(1)
……
一般地, ,请证明这个结论;
(2)
证明:
2
5
-3
b
证明:因为ab=ab
上式转化为对数式可得logaab=b
证明:因为logaN=logaN
上式转化为对数式可得
课堂小结
1. 对数与指数的关系
(对数是指数的逆运算)
ax = N x=logaN.
指数式化对数式:
logaN=x ax = N.
对数式化指数式:
2. 两个特殊对数值
loga1=0.
logaa=1.
3. 两个特殊对数
以10为底的对数称为常用对数:
log10N = lgN.
logeN = lnN.
以 e 为底的对数称为自然对数:
e=2.71828…
4. 两个对数恒等式
b
课堂达标
1. 求下列各式的值:
(1) log1515; (2) log0.41; (3) log981;
(4) log2.56.25; (5) log7343; (6) log3243.
解:
(1)
log1515 =1.
(2)
log0.41 =0.
(3)
log981 =2.
(4)
log2.56.25 =2.
(5)
log7343 =3.
(6)
log3243 =5.
课堂达标
2. 把下列指数式写成对数式:
(1) 3x=1; (2) (3) 4x=2;
(4) 2x=0.5; (5) 10x=25; (6) 5x=6.
解:
(1)
log31=x.
(2)
(3)
log42=x.
(4)
log20.5=x.
(5)
lg25=x.
(6)
log56=x.
谢谢
4.2.1对数的概念
学习目标
情景引入
光在某种介质中传播,每经过1cm,其强度减弱为原来的一半,假设最初的强度是1,写出光的强度y关于介质厚度x的函数关系式
问题一:经过 2 cm后,光的强度是多少?
问题二:经过多少cm,强度为 ?
1cm
1cm
指数运算
,则
(一种新运算)
复习引入
观察数的运算的发展,思考问题:
(1)已知a+x=N,求 x
引入减法
x=N-a
(2)已知ax=N , 求 x
引入除法
(3)已知 ,求 x
引入开方
(4)已知 ,求 x
引入什么?
对数!
概念形成
对数的定义:
一般地,如果 ,那么数x叫做以a为底N的对数(logarithm),记作 .
其中a叫做对数的底数,N叫做真数,读作:以a为底N的对数.
表示一种运算
概念巩固
利用下表解下列方程
合作探究
1. 式子 和 有什么关系?a,x,N 在两个式子中分别代表什么?
3. 零与负数有没有对数?
2. 为什么定义中规定 ?
合作探究
1. 式子 和 有什么关系?a,x,N 在两个式子中分别代表什么?
3. 零与负数有没有对数?
2. 为什么定义中规定 ?
底数
底数
指数
对数
幂
真数
?
数学应用
1、写出所有对数,其中底数和真数A 的元素;
集合A
-1,0,1,2,e,4,10
)
数学应用
1、写出所有对数,其中底数和真数A 的元素;
集合A
-1,0,1,2,e,4,10
=1
=1
=1
=1
=0
=0
=0
=0
=0.5
=2
计算器
2、求出所写对数的值或者它表示什么;
课堂小结
常用对数
自然对数
)
数学应用
1、写出所有对数,其中底数和真数A 的元素;
集合A
-1,0,1,2,e,4,10
=1
=1
=1
=1
=0
=0
=0
=0
=0.5
=2
计算器
2、求出所写对数的值或者它表示什么;
计算器
计算器
计算器
计算器
计算器
转化为常用对数
数学应用
1、写出所有对数,其中底数和真数A 的元素;
集合A
-1,0,1,2,e,4,10
=1
=1
=1
=1
=0
=0
=0
=0
=0.5
=2
计算器
2、求出所写对数的值或者它表示什么;
计算器
计算器
计算器
计算器
计算器
3、对数 , 有什么特点?
1 的对数等于0 (loga1=0).
底的对数等于1 (logaa=1).
数学应用
例1. 求下列各式中 x 的值:
(1) (2) logx8=6; (3) lg100=x; (4) -lne2=x.
解:
(1)
由 得
(2)
由 logx8=6 得
x6=8,
(3)
(4)
由 lg100=x 得
10x=100,
∴ x=2.
由 -lne2=x 得
e-x=e2,
lne2= -x,
化成指数式得
则 x= -2.
另解:x=lg100
=lg102
=2
另解:x=-lne2
=-2
课堂小结
解题总结:
1、指数式与对数式的互化
2、真数幂化
数学应用
例2. 求下列各式的值:
(1) log525; (2) (3) lg1000; (4) lg0.001.
解:
(1)
设 log525=x,
则 5x=25,
即得 x=2,
∴ log525 =2.
(2)
设
则
即得 x= -4,
(3)
设 lg1000=x,
则 10x=1000,
即得 x=3,
∴ lg1000 =3.
(4)
设 lg0.001=x,
则 10x=0.001,
即得 x= -3,
∴ lg0.001 = -3.
另解: log525
=log552
=2
合作探究
P83 T7、已知
(1)
……
一般地, ,请证明这个结论;
(2)
证明:
2
5
-3
b
证明:因为ab=ab
上式转化为对数式可得logaab=b
证明:因为logaN=logaN
上式转化为对数式可得
课堂小结
1. 对数与指数的关系
(对数是指数的逆运算)
ax = N x=logaN.
指数式化对数式:
logaN=x ax = N.
对数式化指数式:
2. 两个特殊对数值
loga1=0.
logaa=1.
3. 两个特殊对数
以10为底的对数称为常用对数:
log10N = lgN.
logeN = lnN.
以 e 为底的对数称为自然对数:
e=2.71828…
4. 两个对数恒等式
b
课堂达标
1. 求下列各式的值:
(1) log1515; (2) log0.41; (3) log981;
(4) log2.56.25; (5) log7343; (6) log3243.
解:
(1)
log1515 =1.
(2)
log0.41 =0.
(3)
log981 =2.
(4)
log2.56.25 =2.
(5)
log7343 =3.
(6)
log3243 =5.
课堂达标
2. 把下列指数式写成对数式:
(1) 3x=1; (2) (3) 4x=2;
(4) 2x=0.5; (5) 10x=25; (6) 5x=6.
解:
(1)
log31=x.
(2)
(3)
log42=x.
(4)
log20.5=x.
(5)
lg25=x.
(6)
log56=x.
谢谢
同课章节目录
- 第1章 集合
- 1.1 集合的概念与表示
- 1.2 子集、全集、补集
- 1.3 交集、并集
- 第2章 常用逻辑用语
- 2.1 命题、定理、定义
- 2.2 充分条件、必要条件、冲要条件
- 2.3 全称量词命题与存在量词命题
- 第3章 不等式
- 3.1 不等式的基本性质
- 3.2 基本不等式
- 3.3 从函数观点看一元二次方程和一元二次不等式
- 第4章 指数与对数
- 4.1 指数
- 4.2 对数
- 第5章 函数概念与性质
- 5.1 函数的概念和图象
- 5.2 函数的表示方法
- 5.3 函数的单调性
- 5.4 函数的奇偶性
- 第6章 幂函数、指数函数和对数函数
- 6.1 幂函数
- 6.2 指数函数
- 6.3 对数函数
- 第7章 三角函数
- 7.1 角与弧度
- 7.2 三角函数概念
- 7.3 三角函数的图象和性质
- 7.4 三角函数应用
- 第8章 函数应用
- 8.1 二分法与求方程近似解
- 8.2 函数与数学模型
