第1章《勾股定理》考点分层练(无答案) 2023--2024学年北师大版八年级上册数学
文档属性
| 名称 | 第1章《勾股定理》考点分层练(无答案) 2023--2024学年北师大版八年级上册数学 |  | |
| 格式 | docx | ||
| 文件大小 | 336.0KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-09-13 11:31:47 | ||
图片预览

文档简介
北师大版八年级上册数学《勾股定理》考点分层练
A层(基础题)
选择题。
题号 1 2 3 4 5
选项
1.如图,有一个水池,水面是一个边长为尺的正方形,在水池的中央有一根新生的芦苇,它高出水面尺,如果把这根芦苇垂直拉向岸边,它的顶端恰好到达岸边的水面,则这个水池的深度是尺.( )
A. B. C. D.
2. 如图,点,都在格点上,若,则的长为( )
A. B. C. D.
3. △ABC的三个内角满足下列条件:①∠A:∠B:∠C=3:4:5;②∠B+∠C=∠A;③AB:BC:AC=1:2:3.其中能判定△ABC是直角三角形的为( )
A.①②③ B.② C.①③ D.②③
4. 如图,一支铅笔放在圆柱体笔筒中,笔筒的内部底面直径是9cm,内壁高12cm.若这支铅笔长为18cm,则这只铅笔在笔筒外面部分长度不可能的是( )
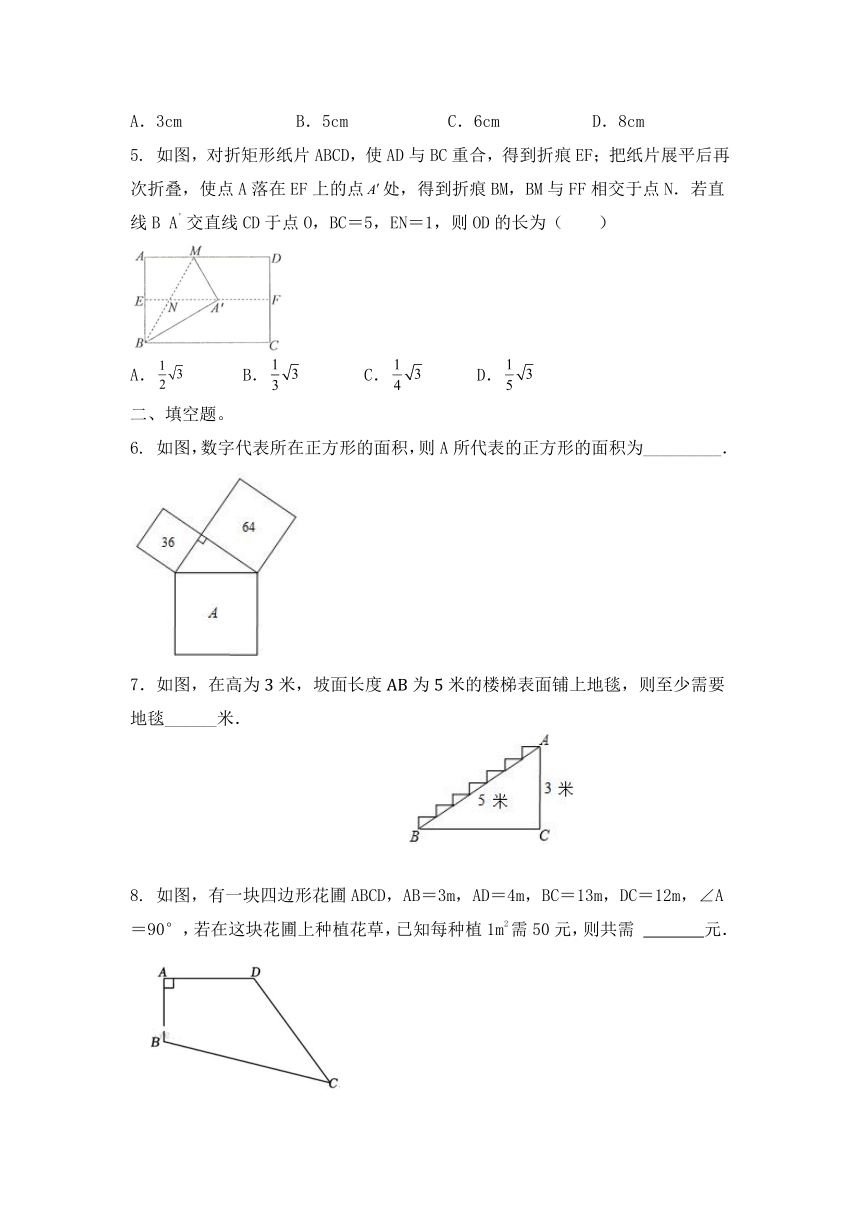
A.3cm B.5cm C.6cm D.8cm
5. 如图,对折矩形纸片ABCD,使AD与BC重合,得到折痕EF;把纸片展平后再次折叠,使点A落在EF上的点处,得到折痕BM,BM与FF相交于点N.若直线B A’交直线CD于点O,BC=5,EN=1,则OD的长为( )
B. C. D.
二、填空题。
6. 如图,数字代表所在正方形的面积,则A所代表的正方形的面积为_________.
7.如图,在高为米,坡面长度为米的楼梯表面铺上地毯,则至少需要地毯______米.
8. 如图,有一块四边形花圃ABCD,AB=3m,AD=4m,BC=13m,DC=12m,∠A=90°,若在这块花圃上种植花草,已知每种植1m2需50元,则共需 元.
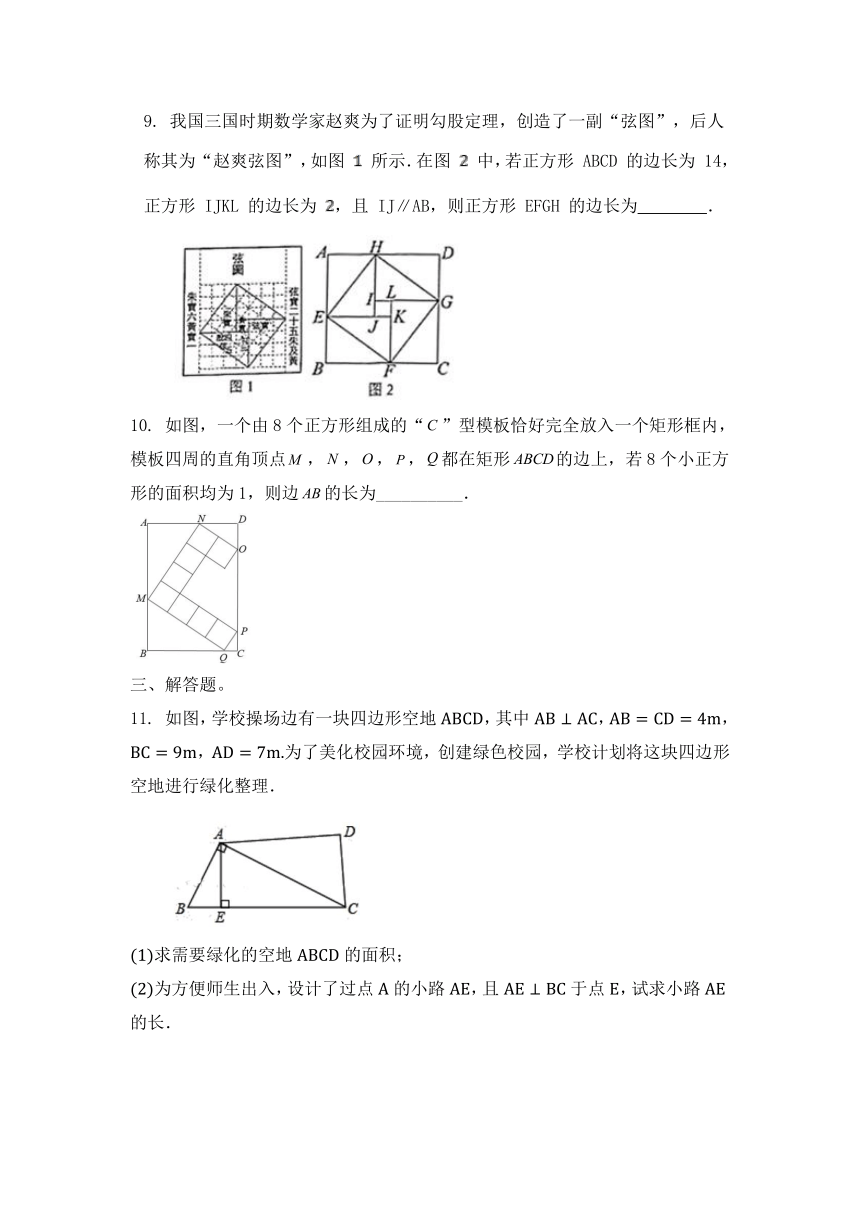
9. 我国三国时期数学家赵爽为了证明勾股定理,创造了一副“弦图”,后人称其为“赵爽弦图”,如图 所示.在图 中,若正方形 ABCD 的边长为 14,正方形 IJKL 的边长为 ,且 IJ∥AB,则正方形 EFGH 的边长为 .
10. 如图,一个由8个正方形组成的“”型模板恰好完全放入一个矩形框内,模板四周的直角顶点,,,,都在矩形的边上,若8个小正方形的面积均为1,则边的长为__________.
三、解答题。
11. 如图,学校操场边有一块四边形空地,其中,,,为了美化校园环境,创建绿色校园,学校计划将这块四边形空地进行绿化整理.
求需要绿化的空地的面积;
为方便师生出入,设计了过点的小路,且于点,试求小路的长.
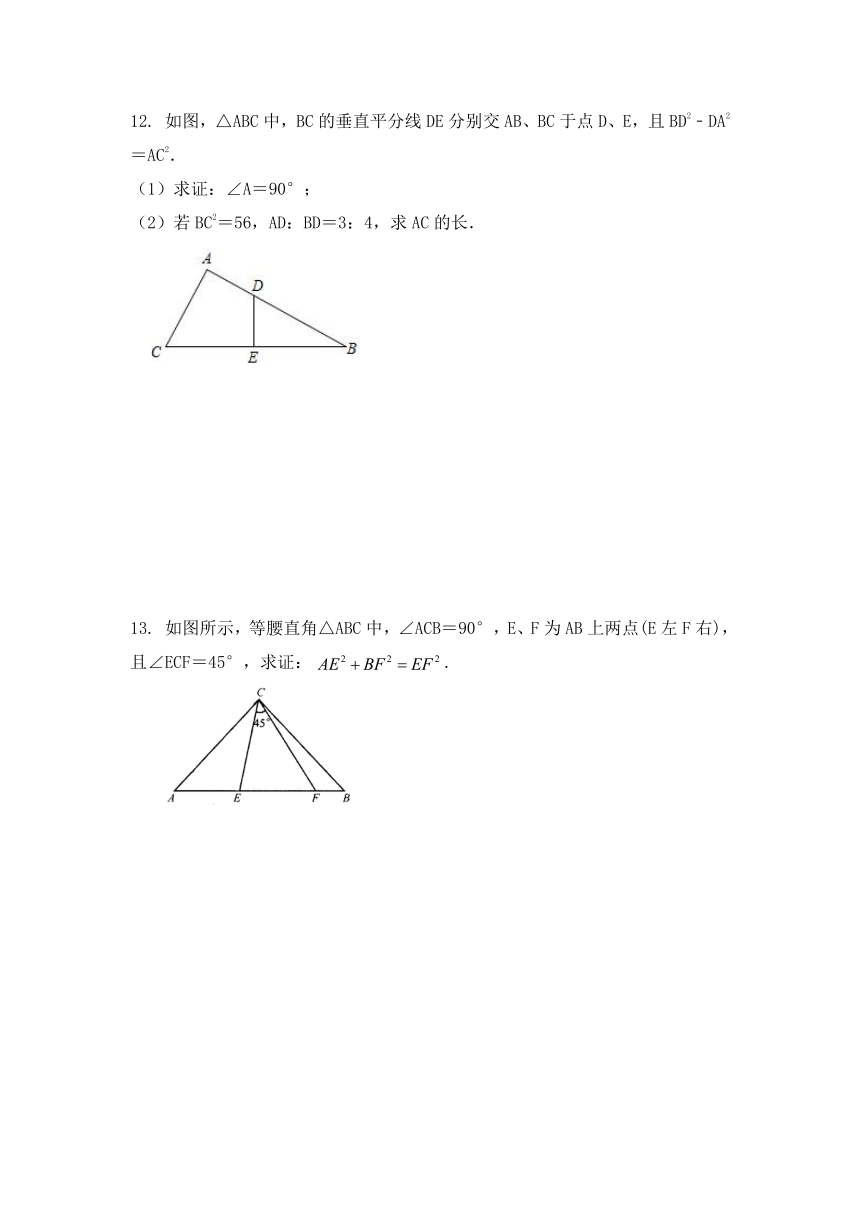
12. 如图,△ABC中,BC的垂直平分线DE分别交AB、BC于点D、E,且BD2﹣DA2=AC2.
(1)求证:∠A=90°;
(2)若BC2=56,AD:BD=3:4,求AC的长.
13. 如图所示,等腰直角△ABC中,∠ACB=90°,E、F为AB上两点(E左F右),且∠ECF=45°,求证:.
B层(提升题)
选择题。
题号 1 2 3 4 5
选项
1. 如图所示,有一块直角三角形纸片,∠C=90°,AC=12cm,BC=9cm,将斜边AB翻折使点B落在直角边AC的延长线上的点E处,折痕为AD,则CD的长为( )
A.3cm B.4cm C.5cm D.cm
2. 若直角三角形的两边长分别是方程的两根,则该直角三角形的面积是( )
A.6 B.12 C.12或 D.6或
3. 如图是我国古代著名的“赵爽弦图”的示意图,此图是由四个全等的直角三角形拼接而成,其中AE=10,BE=24,则EF的长是( )
A.14 B.16 C.14 D.14
4. 如图1,矩形中,点为的中点,点沿从点运动到点,设,两点间的距离为,,图2是点运动时随变化的关系图象,则的长为( )
5. 如图,矩形纸片,点M、N分别在矩形的边、上,将矩形纸片沿直线折叠,使点C落在矩形的边上,记为点P,点D落在G处,连接,交于点Q,连接.下列结论:①四边形是菱形;②点P与点A重合时,;③△PQM的面积S的取值范围是.其中所有正确结论的序号是( )
A.①②③ B.①② C.①③ D.②③
二、填空题。
6. 如图,在△ABC中,∠C=90°,DE⊥AB于D,交AC于点E,若BC=BD,AC=6cm,BC=8cm,AB=10cm,则△ADE的周长是 .
7.如图,在直角坐标系中,点A,B的坐标为A(0,2),B(﹣1,0),将△ABO绕点O按顺时针旋转得到△A1B1O,若AB⊥OB1,则点A1的坐标为 。
8. 如图,把某矩形纸片ABCD沿EF、GH折叠(点E、H在AD边上,点F、G在BC边上),使得点B、点C落在AD边上同一点P处,A点的对称点为点,D点的对称点为点,若∠FPG=90°,△AEP的面积为4,△DPH的面积为1,则矩形ABCD的面积等于_____.
9. 如图,在Rt△ABC中,∠A=30°,∠C=90°,AB=6,点P是线段AC上一动点,点M在线段AB上,当AM=AB时,PB+PM的最小值为 。
10. 如图,在正方形外取一点,连接,,,过点作的垂线交于点,若,.下列结论:①;②;③点到直线的距离为;④,其中正确结论的序号为______.
三、解答题。
11. 如图,Rt△ABC中,∠B=90°,AB=3,BC=4,将△ABC折叠,使点B恰好落在斜边AC上,与点B′重合,AD为折痕,求DB′的长.
12. 在矩形ABCD中,AB=6,BC=8,点E是射线BC上一个动点,连接AE并延长交射线DC于点F,将△ABE沿直线AE翻折到△AB'E,延长AB'与直线CD交于点M.
(1)求证:AM=MF;
(2)当点E是边BC的中点时,求CM的长;
(3)当CF=4时,求CM的长.
13. 定义,我们把对角线互相垂直的四边形叫做垂美四边形.
概念理解:如图②,在四边形ABCD中,如果AB=AD,CB=CD,那么四边形ABCD是垂美四边形吗?请说明理由.
性质探究:如图①,垂美四边形ABCD两组对边AB、CD与BC、AD之间有怎样的数量关系?写出你的猜想,并给出证明.
问题解决:如图③,分别以Rt△ACB的直角边AC和斜边AB为边向外作正方形ACFG和正方形ABDE,连接CE、BG、GE.若AC=2,AB=5,则
(1)求证:△AGB≌△ACE;(2)GE= .
A层(基础题)
选择题。
题号 1 2 3 4 5
选项
1.如图,有一个水池,水面是一个边长为尺的正方形,在水池的中央有一根新生的芦苇,它高出水面尺,如果把这根芦苇垂直拉向岸边,它的顶端恰好到达岸边的水面,则这个水池的深度是尺.( )
A. B. C. D.
2. 如图,点,都在格点上,若,则的长为( )
A. B. C. D.
3. △ABC的三个内角满足下列条件:①∠A:∠B:∠C=3:4:5;②∠B+∠C=∠A;③AB:BC:AC=1:2:3.其中能判定△ABC是直角三角形的为( )
A.①②③ B.② C.①③ D.②③
4. 如图,一支铅笔放在圆柱体笔筒中,笔筒的内部底面直径是9cm,内壁高12cm.若这支铅笔长为18cm,则这只铅笔在笔筒外面部分长度不可能的是( )
A.3cm B.5cm C.6cm D.8cm
5. 如图,对折矩形纸片ABCD,使AD与BC重合,得到折痕EF;把纸片展平后再次折叠,使点A落在EF上的点处,得到折痕BM,BM与FF相交于点N.若直线B A’交直线CD于点O,BC=5,EN=1,则OD的长为( )
B. C. D.
二、填空题。
6. 如图,数字代表所在正方形的面积,则A所代表的正方形的面积为_________.
7.如图,在高为米,坡面长度为米的楼梯表面铺上地毯,则至少需要地毯______米.
8. 如图,有一块四边形花圃ABCD,AB=3m,AD=4m,BC=13m,DC=12m,∠A=90°,若在这块花圃上种植花草,已知每种植1m2需50元,则共需 元.
9. 我国三国时期数学家赵爽为了证明勾股定理,创造了一副“弦图”,后人称其为“赵爽弦图”,如图 所示.在图 中,若正方形 ABCD 的边长为 14,正方形 IJKL 的边长为 ,且 IJ∥AB,则正方形 EFGH 的边长为 .
10. 如图,一个由8个正方形组成的“”型模板恰好完全放入一个矩形框内,模板四周的直角顶点,,,,都在矩形的边上,若8个小正方形的面积均为1,则边的长为__________.
三、解答题。
11. 如图,学校操场边有一块四边形空地,其中,,,为了美化校园环境,创建绿色校园,学校计划将这块四边形空地进行绿化整理.
求需要绿化的空地的面积;
为方便师生出入,设计了过点的小路,且于点,试求小路的长.
12. 如图,△ABC中,BC的垂直平分线DE分别交AB、BC于点D、E,且BD2﹣DA2=AC2.
(1)求证:∠A=90°;
(2)若BC2=56,AD:BD=3:4,求AC的长.
13. 如图所示,等腰直角△ABC中,∠ACB=90°,E、F为AB上两点(E左F右),且∠ECF=45°,求证:.
B层(提升题)
选择题。
题号 1 2 3 4 5
选项
1. 如图所示,有一块直角三角形纸片,∠C=90°,AC=12cm,BC=9cm,将斜边AB翻折使点B落在直角边AC的延长线上的点E处,折痕为AD,则CD的长为( )
A.3cm B.4cm C.5cm D.cm
2. 若直角三角形的两边长分别是方程的两根,则该直角三角形的面积是( )
A.6 B.12 C.12或 D.6或
3. 如图是我国古代著名的“赵爽弦图”的示意图,此图是由四个全等的直角三角形拼接而成,其中AE=10,BE=24,则EF的长是( )
A.14 B.16 C.14 D.14
4. 如图1,矩形中,点为的中点,点沿从点运动到点,设,两点间的距离为,,图2是点运动时随变化的关系图象,则的长为( )
5. 如图,矩形纸片,点M、N分别在矩形的边、上,将矩形纸片沿直线折叠,使点C落在矩形的边上,记为点P,点D落在G处,连接,交于点Q,连接.下列结论:①四边形是菱形;②点P与点A重合时,;③△PQM的面积S的取值范围是.其中所有正确结论的序号是( )
A.①②③ B.①② C.①③ D.②③
二、填空题。
6. 如图,在△ABC中,∠C=90°,DE⊥AB于D,交AC于点E,若BC=BD,AC=6cm,BC=8cm,AB=10cm,则△ADE的周长是 .
7.如图,在直角坐标系中,点A,B的坐标为A(0,2),B(﹣1,0),将△ABO绕点O按顺时针旋转得到△A1B1O,若AB⊥OB1,则点A1的坐标为 。
8. 如图,把某矩形纸片ABCD沿EF、GH折叠(点E、H在AD边上,点F、G在BC边上),使得点B、点C落在AD边上同一点P处,A点的对称点为点,D点的对称点为点,若∠FPG=90°,△AEP的面积为4,△DPH的面积为1,则矩形ABCD的面积等于_____.
9. 如图,在Rt△ABC中,∠A=30°,∠C=90°,AB=6,点P是线段AC上一动点,点M在线段AB上,当AM=AB时,PB+PM的最小值为 。
10. 如图,在正方形外取一点,连接,,,过点作的垂线交于点,若,.下列结论:①;②;③点到直线的距离为;④,其中正确结论的序号为______.
三、解答题。
11. 如图,Rt△ABC中,∠B=90°,AB=3,BC=4,将△ABC折叠,使点B恰好落在斜边AC上,与点B′重合,AD为折痕,求DB′的长.
12. 在矩形ABCD中,AB=6,BC=8,点E是射线BC上一个动点,连接AE并延长交射线DC于点F,将△ABE沿直线AE翻折到△AB'E,延长AB'与直线CD交于点M.
(1)求证:AM=MF;
(2)当点E是边BC的中点时,求CM的长;
(3)当CF=4时,求CM的长.
13. 定义,我们把对角线互相垂直的四边形叫做垂美四边形.
概念理解:如图②,在四边形ABCD中,如果AB=AD,CB=CD,那么四边形ABCD是垂美四边形吗?请说明理由.
性质探究:如图①,垂美四边形ABCD两组对边AB、CD与BC、AD之间有怎样的数量关系?写出你的猜想,并给出证明.
问题解决:如图③,分别以Rt△ACB的直角边AC和斜边AB为边向外作正方形ACFG和正方形ABDE,连接CE、BG、GE.若AC=2,AB=5,则
(1)求证:△AGB≌△ACE;(2)GE= .
同课章节目录
- 第一章 勾股定理
- 1 探索勾股定理
- 2 一定是直角三角形吗
- 3 勾股定理的应用
- 第二章 实数
- 1 认识无理数
- 2 平方根
- 3 立方根
- 4 估算
- 5 用计算器开方
- 6 实数
- 7 二次根式
- 第三章 位置与坐标
- 1 确定位置
- 2 平面直角坐标系
- 3 轴对称与坐标变化
- 第四章 一次函数
- 1 函数
- 2 一次函数与正比例函数
- 3 一次函数的图象
- 4 一次函数的应用
- 第五章 二元一次方程组
- 1 认识二元一次方程组
- 2 求解二元一次方程组
- 3 应用二元一次方程组——鸡免同笼
- 4 应用二元一次方程组——增收节支
- 5 应用二元一次方程组——里程碑上的数
- 6 二元一次方程与一次函数
- 7 用二元一次方程组确定一次函数表达式
- 8*三元一次方程组
- 第六章 数据的分析
- 1 平均数
- 2 中位数与众数
- 3 从统计图分析数据的集中趋势
- 4 数据的离散程度
- 第七章 平行线的证明
- 1 为什么要证明
- 2 定义与命题
- 3 平行线的判定
- 4 平行线的性质
- 5 三角形的内角和定理
