人教版八年级数学上册 14.2整式乘法公式 同步练习 (含答案)
文档属性
| 名称 | 人教版八年级数学上册 14.2整式乘法公式 同步练习 (含答案) |  | |
| 格式 | docx | ||
| 文件大小 | 439.7KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-09-13 14:56:36 | ||
图片预览



文档简介
14.2整式乘法公式同步练习 人教版数学八年级上册
一.选择题(共8小题)
1.计算的结果是
A. B. C. D.
2.下列各式中,不能用乘法公式计算的是 (注乘法公式是指平方差公式或完全平方公式)
A. B.
C. D.
3.若,则的值为
A. B.2 C.1 D.
4.已知,则的值为
A.2 B. C. D.4
5.已知,则代数式的值是
A.16 B.20 C.25 D.30
6.图(1)是一个长为,宽为的长方形,用剪刀沿图中虚线(对称轴)剪开,把它分成四块形状和大小都一样的小长方形,然后按图(2)那样拼成一个正方形,则中间空余的部分的面积是
A. B. C. D.
7.如图,是利用割补法求图形面积的示意图,下列公式中与之相对应的是
A. B.
C. D.
8.设有边长分别为和的类和类正方形纸片、长为宽为的类矩形纸片若干张.如图所示要拼一个边长为的正方形,需要1张类纸片、1张类纸片和2张类纸片.若要拼一个长为、宽为的矩形,则需要类纸片的张数为
A.6 B.7 C.8 D.9
二.填空题(共8小题)
9.已知关于的多项式是一个完全平方式,则的值为 .
10.已知,,则 .
11.若,则代数式的值为 .
12.若是关于的完全平方式,则 .
13.已知代数式是一个完全平方式,则实数的值为 .
14.定义※,例如2※.则※的结果为 .
15.计算的结果的个位数是 .
16.如图,两个正方形的边长分别为和,如果,那么阴影部分的面积是 .
三.简答题(共5小题)
17.化简:.
18.运用乘法公式计算:
(1)
(2)
19.已知正实数、,满足,.
(1)求的值;
(2)若时,是完全平方式,求的值.
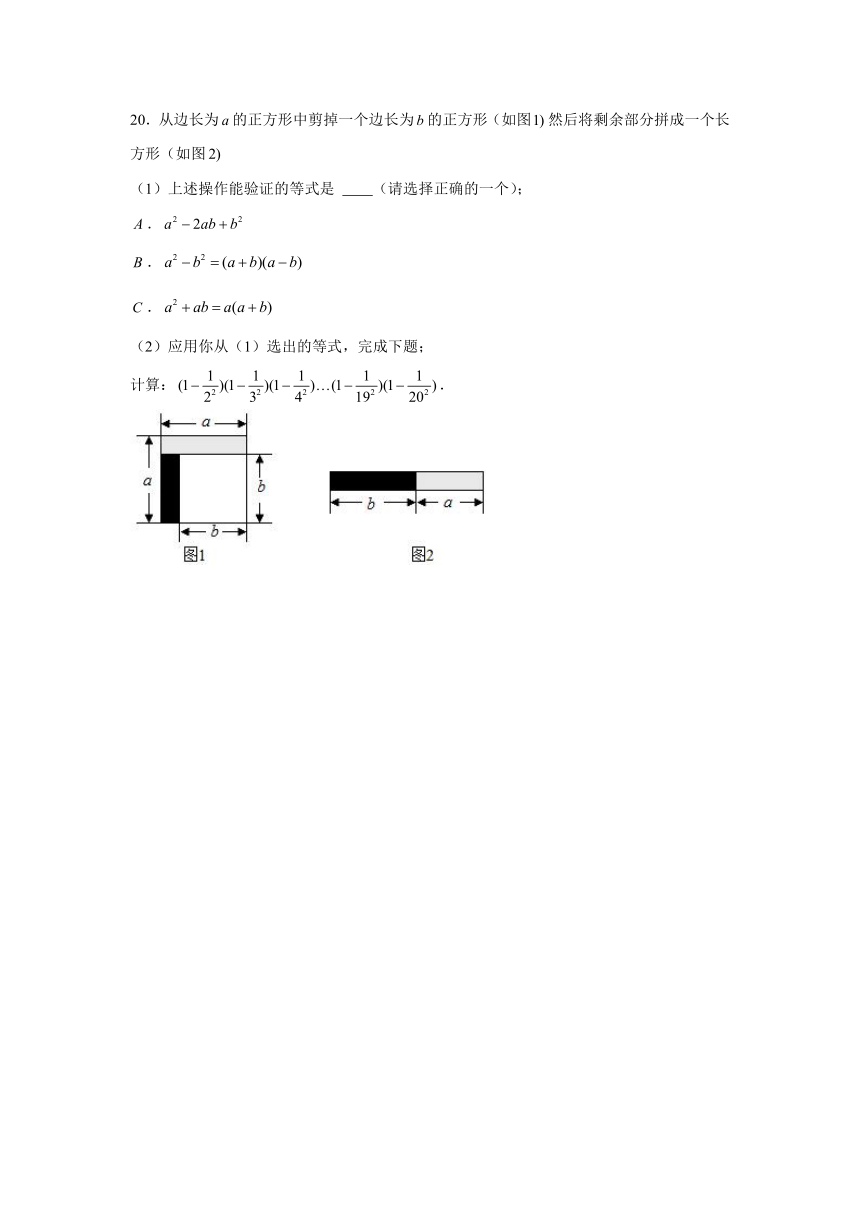
20.从边长为的正方形中剪掉一个边长为的正方形(如图然后将剩余部分拼成一个长方形(如图
(1)上述操作能验证的等式是 (请选择正确的一个);
.
.
.
(2)应用你从(1)选出的等式,完成下题;
计算:.
21.数学活动课上,老师把一个边长为的正方形分割成4块,如图所示.
(1)请用两种不同的方法表示出图中大正方形的面积:方法 ;方法 .
(2)观察图形,请你写出代数式、、之间的等量关系: .
(3)根据(2)题中的等量关系,解决如下问题:
①已知,,求的值;
②若,求的值.
答案版:
一.选择题(共8小题)
题号 1 2 3 4 5 6 7 8
答案 D A C A C C A C
二.填空题(共8小题)
9.答案为:9.
10.答案为:2.
11.答案为:4
12.答案为:或7.
13.答案为:或.
14.答案为:.
15.答案为:6
16.答案为:27.
三.解答题(共58小题)
17.化简:.
【解答】解:原式
.
18.运用乘法公式计算:
(1)
(2)
【解答】解:(1);
(2).
19.已知正实数、,满足,.
(1)求的值;
(2)若时,是完全平方式,求的值.
【解答】解:(1),
,
.
(2),
,
是完全平方式,
,
.
20.从边长为的正方形中剪掉一个边长为的正方形(如图然后将剩余部分拼成一个长方形(如图
(1)上述操作能验证的等式是 (请选择正确的一个);
.
.
.
(2)应用你从(1)选出的等式,完成下题;
计算:.
【解答】解:(1)图1中阴影部分的面积是两个正方形的面积差,即,
拼成的图2为长为,宽为的长方形,因此面积为,
所以有,
故答案为:;
(2)原式
.
21.数学活动课上,老师把一个边长为的正方形分割成4块,如图所示.
(1)请用两种不同的方法表示出图中大正方形的面积:方法 ;方法 .
(2)观察图形,请你写出代数式、、之间的等量关系: .
(3)根据(2)题中的等量关系,解决如下问题:
①已知,,求的值;
②若,求的值.
【解答】解:(1)由题意得,该正方形的面积可表示为或,
故答案为:,;
(2)由(1)题可得,
即,
故答案为:;
(3)①由(2)题结果可得,
,
当,时,
,
即的值是11;
②由(2)题结果可得,
,
,
,
,
,
即的值是14.
一.选择题(共8小题)
1.计算的结果是
A. B. C. D.
2.下列各式中,不能用乘法公式计算的是 (注乘法公式是指平方差公式或完全平方公式)
A. B.
C. D.
3.若,则的值为
A. B.2 C.1 D.
4.已知,则的值为
A.2 B. C. D.4
5.已知,则代数式的值是
A.16 B.20 C.25 D.30
6.图(1)是一个长为,宽为的长方形,用剪刀沿图中虚线(对称轴)剪开,把它分成四块形状和大小都一样的小长方形,然后按图(2)那样拼成一个正方形,则中间空余的部分的面积是
A. B. C. D.
7.如图,是利用割补法求图形面积的示意图,下列公式中与之相对应的是
A. B.
C. D.
8.设有边长分别为和的类和类正方形纸片、长为宽为的类矩形纸片若干张.如图所示要拼一个边长为的正方形,需要1张类纸片、1张类纸片和2张类纸片.若要拼一个长为、宽为的矩形,则需要类纸片的张数为
A.6 B.7 C.8 D.9
二.填空题(共8小题)
9.已知关于的多项式是一个完全平方式,则的值为 .
10.已知,,则 .
11.若,则代数式的值为 .
12.若是关于的完全平方式,则 .
13.已知代数式是一个完全平方式,则实数的值为 .
14.定义※,例如2※.则※的结果为 .
15.计算的结果的个位数是 .
16.如图,两个正方形的边长分别为和,如果,那么阴影部分的面积是 .
三.简答题(共5小题)
17.化简:.
18.运用乘法公式计算:
(1)
(2)
19.已知正实数、,满足,.
(1)求的值;
(2)若时,是完全平方式,求的值.
20.从边长为的正方形中剪掉一个边长为的正方形(如图然后将剩余部分拼成一个长方形(如图
(1)上述操作能验证的等式是 (请选择正确的一个);
.
.
.
(2)应用你从(1)选出的等式,完成下题;
计算:.
21.数学活动课上,老师把一个边长为的正方形分割成4块,如图所示.
(1)请用两种不同的方法表示出图中大正方形的面积:方法 ;方法 .
(2)观察图形,请你写出代数式、、之间的等量关系: .
(3)根据(2)题中的等量关系,解决如下问题:
①已知,,求的值;
②若,求的值.
答案版:
一.选择题(共8小题)
题号 1 2 3 4 5 6 7 8
答案 D A C A C C A C
二.填空题(共8小题)
9.答案为:9.
10.答案为:2.
11.答案为:4
12.答案为:或7.
13.答案为:或.
14.答案为:.
15.答案为:6
16.答案为:27.
三.解答题(共58小题)
17.化简:.
【解答】解:原式
.
18.运用乘法公式计算:
(1)
(2)
【解答】解:(1);
(2).
19.已知正实数、,满足,.
(1)求的值;
(2)若时,是完全平方式,求的值.
【解答】解:(1),
,
.
(2),
,
是完全平方式,
,
.
20.从边长为的正方形中剪掉一个边长为的正方形(如图然后将剩余部分拼成一个长方形(如图
(1)上述操作能验证的等式是 (请选择正确的一个);
.
.
.
(2)应用你从(1)选出的等式,完成下题;
计算:.
【解答】解:(1)图1中阴影部分的面积是两个正方形的面积差,即,
拼成的图2为长为,宽为的长方形,因此面积为,
所以有,
故答案为:;
(2)原式
.
21.数学活动课上,老师把一个边长为的正方形分割成4块,如图所示.
(1)请用两种不同的方法表示出图中大正方形的面积:方法 ;方法 .
(2)观察图形,请你写出代数式、、之间的等量关系: .
(3)根据(2)题中的等量关系,解决如下问题:
①已知,,求的值;
②若,求的值.
【解答】解:(1)由题意得,该正方形的面积可表示为或,
故答案为:,;
(2)由(1)题可得,
即,
故答案为:;
(3)①由(2)题结果可得,
,
当,时,
,
即的值是11;
②由(2)题结果可得,
,
,
,
,
,
即的值是14.
