【同步培优微专题】专题9 整式的列式运用(3)图形问题(1)(含答案)
文档属性
| 名称 | 【同步培优微专题】专题9 整式的列式运用(3)图形问题(1)(含答案) | 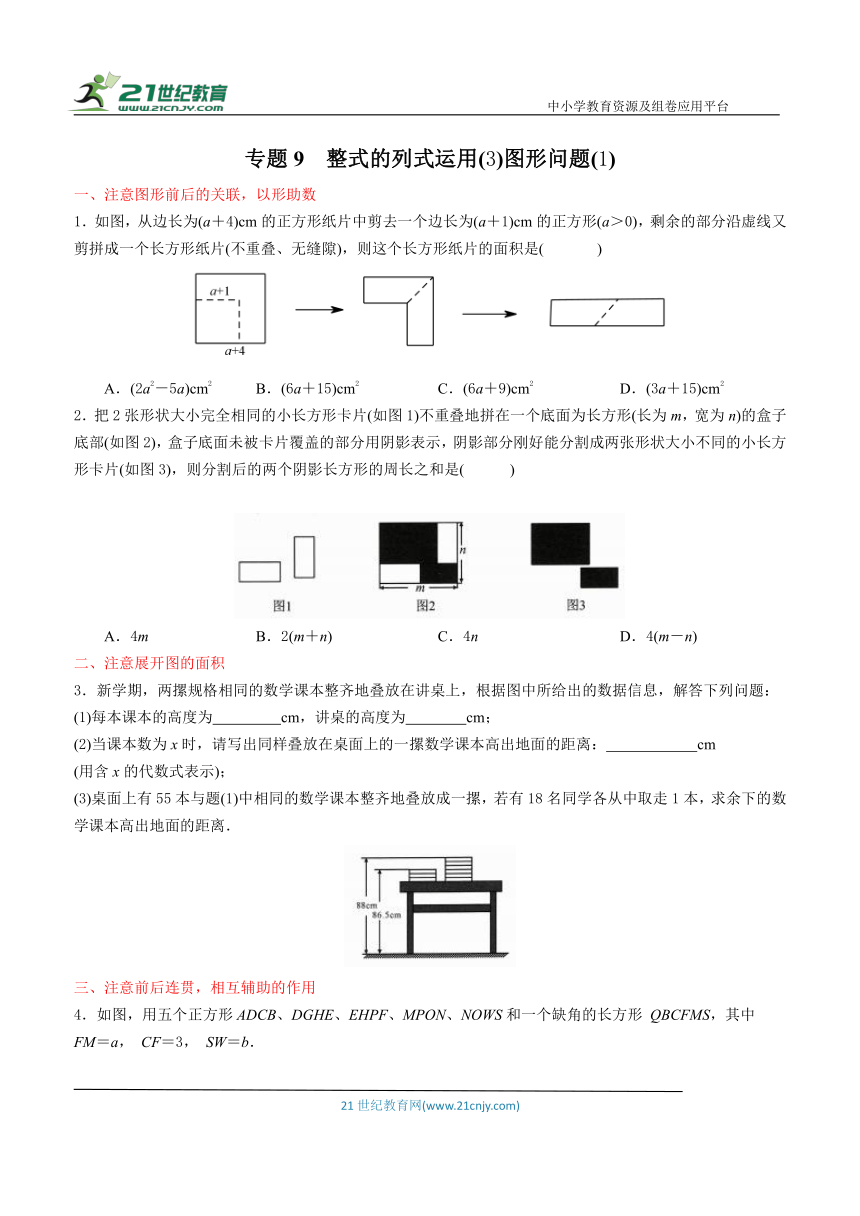 | |
| 格式 | docx | ||
| 文件大小 | 178.9KB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-09-13 15:53:20 | ||
图片预览

文档简介
中小学教育资源及组卷应用平台
专题9 整式的列式运用(3)图形问题(1)
一、注意图形前后的关联,以形助数
1.如图,从边长为(a+4)cm的正方形纸片中剪去一个边长为(a+1)cm的正方形(a>0),剩余的部分沿虚线又剪拼成一个长方形纸片(不重叠、无缝隙),则这个长方形纸片的面积是( )
A.(2a2-5a)cm2 B.(6a+15)cm2 C.(6a+9)cm2 D.(3a+15)cm2
2.把2张形状大小完全相同的小长方形卡片(如图1)不重叠地拼在一个底面为长方形(长为m,宽为n)的盒子底部(如图2),盒子底面未被卡片覆盖的部分用阴影表示,阴影部分刚好能分割成两张形状大小不同的小长方形卡片(如图3),则分割后的两个阴影长方形的周长之和是( )
A.4m B.2(m+n) C.4n D.4(m-n)
二、注意展开图的面积
3.新学期,两摞规格相同的数学课本整齐地叠放在讲桌上,根据图中所给出的数据信息,解答下列问题:
(1)每本课本的高度为 cm,讲桌的高度为 cm;
(2)当课本数为x时,请写出同样叠放在桌面上的一摞数学课本高出地面的距离: cm
(用含x的代数式表示);
(3)桌面上有55本与题(1)中相同的数学课本整齐地叠放成一摞,若有18名同学各从中取走1本,求余下的数学课本高出地面的距离.
三、注意前后连贯,相互辅助的作用
4.如图,用五个正方形ADCB、DGHE、EHPF、MPON、NOWS和一个缺角的长方形 QBCFMS,其中
FM=a, CF=3, SW=b.
(1)求AD的长(用含a和b的式子表示);
(2)求长方形AGWQ的周长(用含a和b的式子表示).
专题9 整式的列式运用(3)图形问题(1)
一、注意图形前后的关联,以形助数
1.如图,从边长为(a+4)cm的正方形纸片中剪去一个边长为(a+1)cm的正方形(a>0),剩余的部分沿虚线又剪拼成一个长方形纸片(不重叠、无缝隙),则这个长方形纸片的面积是( )
A.(2a2-5a)cm2 B.(6a+15)cm2 C.(6a+9)cm2 D.(3a+15)cm2
答案:B
2.把2张形状大小完全相同的小长方形卡片(如图1)不重叠地拼在一个底面为长方形(长为m,宽为n)的盒子底部(如图2),盒子底面未被卡片覆盖的部分用阴影表示,阴影部分刚好能分割成两张形状大小不同的小长方形卡片(如图3),则分割后的两个阴影长方形的周长之和是( )
A.4m B.2(m+n) C.4n D.4(m-n)
答案:A
二、注意展开图的面积
3.新学期,两摞规格相同的数学课本整齐地叠放在讲桌上,根据图中所给出的数据信息,解答下列问题:
(1)每本课本的高度为 cm,讲桌的高度为 cm;
(2)当课本数为x时,请写出同样叠放在桌面上的一摞数学课本高出地面的距离: cm
(用含x的代数式表示);
(3)桌面上有55本与题(1)中相同的数学课本整齐地叠放成一摞,若有18名同学各从中取走1本,求余下的数学课本高出地面的距离.
答案:(1)0.5,85;
(2)∵x本课本的高度为0.5xcm,讲桌的高度为85cm,∴高出地面的距离为(85+0.5x)cm;
(3)当x=55-18=37时,85+0.5x=103.5(cm),故余下的数学课本高出地面的距离是103.5cm.
三、注意前后连贯,相互辅助的作用
4.如图,用五个正方形ADCB、DGHE、EHPF、MPON、NOWS和一个缺角的长方形 QBCFMS,其中
FM=a, CF=3, SW=b.
(1)求AD的长(用含a和b的式子表示);
(2)求长方形AGWQ的周长(用含a和b的式子表示).
答案: (1) PF=a+b, EC=a+b-3,AD=DC=DE+EC=a+b+a+b-3=2a+2b-3;
(2)GW=2GH+2PO=2(a+b)+2b=2a+4b,AG=AD+DG=2a+2b-3+a+b=3a+3b-3,
∴长方形AGWQ的周长为:2AG+2WG=2(3a+3b-3+2a+4b)=10a+14b-6.
21世纪教育网(www.21cnjy.com)
专题9 整式的列式运用(3)图形问题(1)
一、注意图形前后的关联,以形助数
1.如图,从边长为(a+4)cm的正方形纸片中剪去一个边长为(a+1)cm的正方形(a>0),剩余的部分沿虚线又剪拼成一个长方形纸片(不重叠、无缝隙),则这个长方形纸片的面积是( )
A.(2a2-5a)cm2 B.(6a+15)cm2 C.(6a+9)cm2 D.(3a+15)cm2
2.把2张形状大小完全相同的小长方形卡片(如图1)不重叠地拼在一个底面为长方形(长为m,宽为n)的盒子底部(如图2),盒子底面未被卡片覆盖的部分用阴影表示,阴影部分刚好能分割成两张形状大小不同的小长方形卡片(如图3),则分割后的两个阴影长方形的周长之和是( )
A.4m B.2(m+n) C.4n D.4(m-n)
二、注意展开图的面积
3.新学期,两摞规格相同的数学课本整齐地叠放在讲桌上,根据图中所给出的数据信息,解答下列问题:
(1)每本课本的高度为 cm,讲桌的高度为 cm;
(2)当课本数为x时,请写出同样叠放在桌面上的一摞数学课本高出地面的距离: cm
(用含x的代数式表示);
(3)桌面上有55本与题(1)中相同的数学课本整齐地叠放成一摞,若有18名同学各从中取走1本,求余下的数学课本高出地面的距离.
三、注意前后连贯,相互辅助的作用
4.如图,用五个正方形ADCB、DGHE、EHPF、MPON、NOWS和一个缺角的长方形 QBCFMS,其中
FM=a, CF=3, SW=b.
(1)求AD的长(用含a和b的式子表示);
(2)求长方形AGWQ的周长(用含a和b的式子表示).
专题9 整式的列式运用(3)图形问题(1)
一、注意图形前后的关联,以形助数
1.如图,从边长为(a+4)cm的正方形纸片中剪去一个边长为(a+1)cm的正方形(a>0),剩余的部分沿虚线又剪拼成一个长方形纸片(不重叠、无缝隙),则这个长方形纸片的面积是( )
A.(2a2-5a)cm2 B.(6a+15)cm2 C.(6a+9)cm2 D.(3a+15)cm2
答案:B
2.把2张形状大小完全相同的小长方形卡片(如图1)不重叠地拼在一个底面为长方形(长为m,宽为n)的盒子底部(如图2),盒子底面未被卡片覆盖的部分用阴影表示,阴影部分刚好能分割成两张形状大小不同的小长方形卡片(如图3),则分割后的两个阴影长方形的周长之和是( )
A.4m B.2(m+n) C.4n D.4(m-n)
答案:A
二、注意展开图的面积
3.新学期,两摞规格相同的数学课本整齐地叠放在讲桌上,根据图中所给出的数据信息,解答下列问题:
(1)每本课本的高度为 cm,讲桌的高度为 cm;
(2)当课本数为x时,请写出同样叠放在桌面上的一摞数学课本高出地面的距离: cm
(用含x的代数式表示);
(3)桌面上有55本与题(1)中相同的数学课本整齐地叠放成一摞,若有18名同学各从中取走1本,求余下的数学课本高出地面的距离.
答案:(1)0.5,85;
(2)∵x本课本的高度为0.5xcm,讲桌的高度为85cm,∴高出地面的距离为(85+0.5x)cm;
(3)当x=55-18=37时,85+0.5x=103.5(cm),故余下的数学课本高出地面的距离是103.5cm.
三、注意前后连贯,相互辅助的作用
4.如图,用五个正方形ADCB、DGHE、EHPF、MPON、NOWS和一个缺角的长方形 QBCFMS,其中
FM=a, CF=3, SW=b.
(1)求AD的长(用含a和b的式子表示);
(2)求长方形AGWQ的周长(用含a和b的式子表示).
答案: (1) PF=a+b, EC=a+b-3,AD=DC=DE+EC=a+b+a+b-3=2a+2b-3;
(2)GW=2GH+2PO=2(a+b)+2b=2a+4b,AG=AD+DG=2a+2b-3+a+b=3a+3b-3,
∴长方形AGWQ的周长为:2AG+2WG=2(3a+3b-3+2a+4b)=10a+14b-6.
21世纪教育网(www.21cnjy.com)
