2.4.1圆的标准方程 课件(共33张PPT)
文档属性
| 名称 | 2.4.1圆的标准方程 课件(共33张PPT) |  | |
| 格式 | pptx | ||
| 文件大小 | 3.2MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教A版(2019) | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-09-12 14:19:02 | ||
图片预览








文档简介
(共33张PPT)
第二章 直线与圆
朝阳区课程资源·高二下数学
2.4.1 圆的标准方程
1.掌握圆的标准方程,能根据条件求出圆的标准方程,提高运算能力,增强数形结合的意识;
2.经历圆的标准方程的推导过程,进一步探求用代数方法研究几何问题的基本思路,提高探索、推理能力、表达能力.
【学习目标】
我们知道在日常生活中,圆的应用十分广泛,如每条通车隧道的隧道口就是一个半圆形,而在驾驶汽车通过隧道时,我们常常会看到一个限高的标志,这个限高的数据是如何得到的?我们如何从数学的角度给出合理的解释?请大家看以下问题。
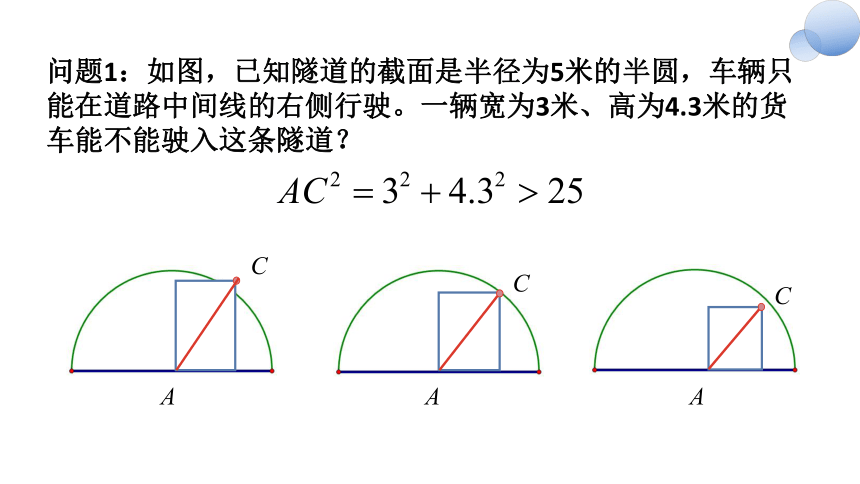
问题1:如图,已知隧道的截面是半径为5米的半圆,车辆只能在道路中间线的右侧行驶。一辆宽为3米、高为4.3米的货车能不能驶入这条隧道?
任务1:请大家将这一现实生活问题抽象出对应的数学问题;
任务2:请大家思考判断货车能否通过隧道的依据是什么?
问题1:如图,已知隧道的截面是半径为5米的半圆,车辆只能在道路中间线的右侧行驶。一辆宽为3米、高为4.3米的货车能不能驶入这条隧道?
问题1:如图,已知隧道的截面是半径为5米的半圆,车辆只能在道路中间线的右侧行驶。一辆宽为3米、高为4.3米的货车能不能驶入这条隧道?
A
A
A
C
C
C
问题2:我们知道,两点确定一条直线,一点和方向也能确定一条直线。什么样的条件确定一个圆呢?
圆心 半径
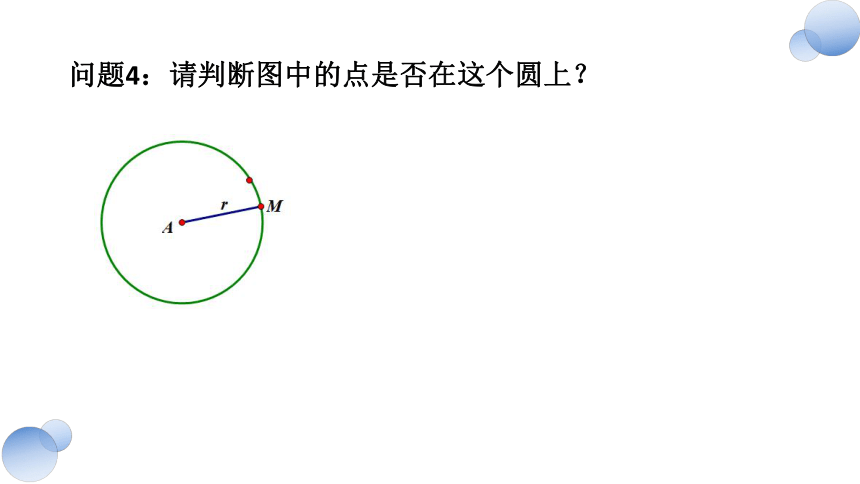
请问满足什么条件的点在这个圆上?你能写出其满足的关系式吗?
问题4:请判断图中的点是否在这个圆上?
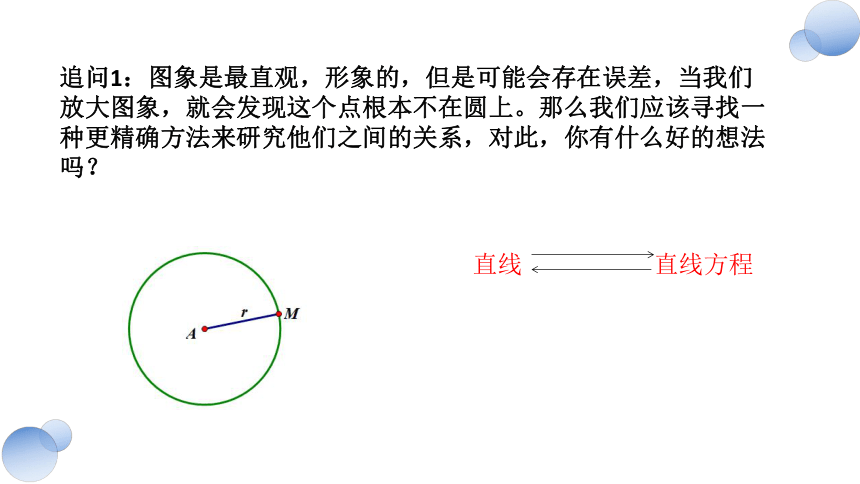
追问1:图象是最直观,形象的,但是可能会存在误差,当我们放大图象,就会发现这个点根本不在圆上。那么我们应该寻找一种更精确方法来研究他们之间的关系,对此,你有什么好的想法吗?
直线 直线方程
类比求直线的点斜式方程的方法来求圆的方程
探究一:在平面直角坐标系中,一个点对应一个坐标
一条直线对应一个二元一次方程 ( 不全为零),
那么圆又对应怎样的方程?如何建立圆的方程?
问题1:请总结出求直线方程的过程的基本步骤
建系
设点
列式
化简
检验
问题2:你能说出求直线的点斜式方程的本质是在求什么吗?
问题3:类比求直线方程的步骤求圆的标准方程,我们需要怎么做?
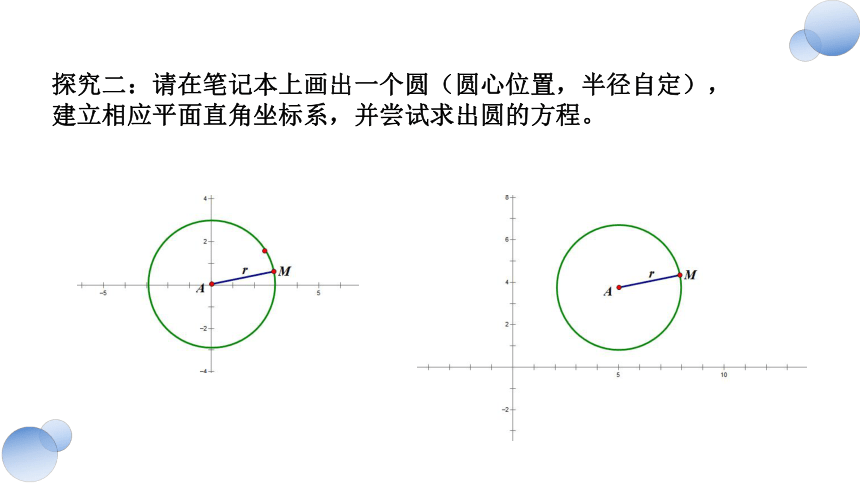
探究二:请在笔记本上画出一个圆(圆心位置,半径自定),建立相应平面直角坐标系,并尝试求出圆的方程。
如图,在平面直角坐标系中,圆A的圆心A ,半径为r
为圆上任意一点,则圆A就是以下点的集合
如图,在平面直角坐标系中,圆A的圆心A ,半径为r
为圆上任意一点,则圆A就是以下点的集合
根据两点间的距离公式,点M的坐标满足的条件可以表示为
如图,在平面直角坐标系中,圆A的圆心A ,半径为r
为圆上任意一点,则圆A就是以下点的集合
根据两点间的距离公式,点M的坐标满足的条件可以表示为
两边平方,得
如图,在平面直角坐标系中,圆A的圆心A ,半径为r
(1)
为圆上任意一点,则圆A就是以下点的集合
根据两点间的距离公式,点M的坐标满足的条件可以表示为
两边平方,得
如图,在平面直角坐标系中,圆A的圆心A ,半径为r
建系
设点
列式
化简
坐标化
检验
问题6:请仔细观察圆的标准方程,写出其在结构上的特征
半径
圆心纵坐标
圆心横坐标
1
例1求圆心为A(2,-3),半径为5的圆的标准方程,并判断点M1(5,-7),M2(-2,-1)是否在这个圆上.
【分析】根据点的坐标与圆的方程的关系,只要判断一个点的坐标是否满足圆的方程,就可以得到这个点是否在圆上.
例1求圆心为A(2,-3),半径为5的圆的标准方程,并判断点M1(5,-7),M2(-2,-1)是否在这个圆上.
解: 圆心为A(2,-3),半径为5的圆的标准方程是
(x-2)2+(y+3)2=25
把点M1(5,-7)的坐标代入方程(x-2)2+(y+3)2=25的左边,
得(5-2)2+(-7+3)2=25,等式成立,所以点M1在这个圆上.
把点M2(-2,-1)的坐标代入方程(x-2)2+(y+3)2=25的左边,
得(-2-2)2+(-1+3)2≠25,等式不成立,所以点M2不在这个圆上.
思考
点M0(x0,y0)在圆C:(x-a)2+(y-b)2=r2内的条件是什么?在圆(x-a)2+(y-b)2=r2外的条件是什么?
C
C
C
M0
M0
M0
(x0-a)2+(y0-b)2(x0-a)2+(y0-b)2=r2
(x0-a)2+(y0-b)2>r2
在圆内
在圆上
在圆外
例2 ABC的三个顶点分别是A(5,1),B(7,-3),C(2,-8),求 ABC的外接圆的标准方程.
分析:不在同一条直线上的三个点可以确定一个圆,三角形有唯一的外接圆.只要确定了a,b,r,圆的标准方程就确定了.
【代数法】: 设所求的方程是 (x-a)2+(y-b)2=r2
把三个点的坐标代入上式,可得
故外接圆的标准方程是
(x-2)2+(y+3)2=25
例2 ABC的三个顶点分别是A(5,1),B(7,-3),C(2,-8),求 ABC的外接圆的标准方程.
【几何法】: (AB与BC中垂线的交点即为圆心)
因为A(5,1),B(7,-3)
所以AB的中点坐标为(6,-1),且kAB=-2
所以AB中垂线的斜率为,
则AB中垂线方程为y+1=(x-6),即x-2y-8=0,
同理可得,BC的中垂线方程为x+y+1=0
联立两个中垂线方程,得圆心坐标为M(2,-3)
所以半径r=|AM|=
故外接圆的标准方程是(x-2)2+(y+3)2=25
A
B
C
例3 已知圆心为C的圆经过A(1,1),B(2,-2)两点,且圆心C在直线l:x-y+1=0上,求此圆的标准方程.
【代数法】: 设所求的方程是 (x-a)2+(y-b)2=r2
把点A,B的坐标代入圆得方程,圆心C(a,b)代入直线l,得
故外接圆的标准方程是(x+3)2+(y+2)2=25
例4 已知圆心为C的圆经过A(1,1),B(2,-2)两点,且圆心C在直线l:x-y+1=0上,求此圆的标准方程.
几何角度:如何确定圆心呢?
x
O
A(1,1)
B(2,-2)
y
圆心
在l上
在AB中垂线上
AB中点
AB斜率
【几何法】: (AB的中垂线与l的交点即为圆心)
因为A(1,1),B(2,-2)
所以AB的中点坐标为(,-),且kAB=-3
所以AB中垂线的斜率为,
则AB中垂线方程为y+=(x-),即x-3y-3=0,
联立中垂线方程与直线l: x-y+1=0,得圆心坐标为M(-3,-2)
所以半径r=|AC|=
故外接圆的标准方程是(x+3)2+(y+2)2=25
x
O
A(1,1)
B(2,-2)
y
通过本节课,你学到了哪些知识?
第二章 直线与圆
朝阳区课程资源·高二下数学
2.4.1 圆的标准方程
1.掌握圆的标准方程,能根据条件求出圆的标准方程,提高运算能力,增强数形结合的意识;
2.经历圆的标准方程的推导过程,进一步探求用代数方法研究几何问题的基本思路,提高探索、推理能力、表达能力.
【学习目标】
我们知道在日常生活中,圆的应用十分广泛,如每条通车隧道的隧道口就是一个半圆形,而在驾驶汽车通过隧道时,我们常常会看到一个限高的标志,这个限高的数据是如何得到的?我们如何从数学的角度给出合理的解释?请大家看以下问题。
问题1:如图,已知隧道的截面是半径为5米的半圆,车辆只能在道路中间线的右侧行驶。一辆宽为3米、高为4.3米的货车能不能驶入这条隧道?
任务1:请大家将这一现实生活问题抽象出对应的数学问题;
任务2:请大家思考判断货车能否通过隧道的依据是什么?
问题1:如图,已知隧道的截面是半径为5米的半圆,车辆只能在道路中间线的右侧行驶。一辆宽为3米、高为4.3米的货车能不能驶入这条隧道?
问题1:如图,已知隧道的截面是半径为5米的半圆,车辆只能在道路中间线的右侧行驶。一辆宽为3米、高为4.3米的货车能不能驶入这条隧道?
A
A
A
C
C
C
问题2:我们知道,两点确定一条直线,一点和方向也能确定一条直线。什么样的条件确定一个圆呢?
圆心 半径
请问满足什么条件的点在这个圆上?你能写出其满足的关系式吗?
问题4:请判断图中的点是否在这个圆上?
追问1:图象是最直观,形象的,但是可能会存在误差,当我们放大图象,就会发现这个点根本不在圆上。那么我们应该寻找一种更精确方法来研究他们之间的关系,对此,你有什么好的想法吗?
直线 直线方程
类比求直线的点斜式方程的方法来求圆的方程
探究一:在平面直角坐标系中,一个点对应一个坐标
一条直线对应一个二元一次方程 ( 不全为零),
那么圆又对应怎样的方程?如何建立圆的方程?
问题1:请总结出求直线方程的过程的基本步骤
建系
设点
列式
化简
检验
问题2:你能说出求直线的点斜式方程的本质是在求什么吗?
问题3:类比求直线方程的步骤求圆的标准方程,我们需要怎么做?
探究二:请在笔记本上画出一个圆(圆心位置,半径自定),建立相应平面直角坐标系,并尝试求出圆的方程。
如图,在平面直角坐标系中,圆A的圆心A ,半径为r
为圆上任意一点,则圆A就是以下点的集合
如图,在平面直角坐标系中,圆A的圆心A ,半径为r
为圆上任意一点,则圆A就是以下点的集合
根据两点间的距离公式,点M的坐标满足的条件可以表示为
如图,在平面直角坐标系中,圆A的圆心A ,半径为r
为圆上任意一点,则圆A就是以下点的集合
根据两点间的距离公式,点M的坐标满足的条件可以表示为
两边平方,得
如图,在平面直角坐标系中,圆A的圆心A ,半径为r
(1)
为圆上任意一点,则圆A就是以下点的集合
根据两点间的距离公式,点M的坐标满足的条件可以表示为
两边平方,得
如图,在平面直角坐标系中,圆A的圆心A ,半径为r
建系
设点
列式
化简
坐标化
检验
问题6:请仔细观察圆的标准方程,写出其在结构上的特征
半径
圆心纵坐标
圆心横坐标
1
例1求圆心为A(2,-3),半径为5的圆的标准方程,并判断点M1(5,-7),M2(-2,-1)是否在这个圆上.
【分析】根据点的坐标与圆的方程的关系,只要判断一个点的坐标是否满足圆的方程,就可以得到这个点是否在圆上.
例1求圆心为A(2,-3),半径为5的圆的标准方程,并判断点M1(5,-7),M2(-2,-1)是否在这个圆上.
解: 圆心为A(2,-3),半径为5的圆的标准方程是
(x-2)2+(y+3)2=25
把点M1(5,-7)的坐标代入方程(x-2)2+(y+3)2=25的左边,
得(5-2)2+(-7+3)2=25,等式成立,所以点M1在这个圆上.
把点M2(-2,-1)的坐标代入方程(x-2)2+(y+3)2=25的左边,
得(-2-2)2+(-1+3)2≠25,等式不成立,所以点M2不在这个圆上.
思考
点M0(x0,y0)在圆C:(x-a)2+(y-b)2=r2内的条件是什么?在圆(x-a)2+(y-b)2=r2外的条件是什么?
C
C
C
M0
M0
M0
(x0-a)2+(y0-b)2
(x0-a)2+(y0-b)2>r2
在圆内
在圆上
在圆外
例2 ABC的三个顶点分别是A(5,1),B(7,-3),C(2,-8),求 ABC的外接圆的标准方程.
分析:不在同一条直线上的三个点可以确定一个圆,三角形有唯一的外接圆.只要确定了a,b,r,圆的标准方程就确定了.
【代数法】: 设所求的方程是 (x-a)2+(y-b)2=r2
把三个点的坐标代入上式,可得
故外接圆的标准方程是
(x-2)2+(y+3)2=25
例2 ABC的三个顶点分别是A(5,1),B(7,-3),C(2,-8),求 ABC的外接圆的标准方程.
【几何法】: (AB与BC中垂线的交点即为圆心)
因为A(5,1),B(7,-3)
所以AB的中点坐标为(6,-1),且kAB=-2
所以AB中垂线的斜率为,
则AB中垂线方程为y+1=(x-6),即x-2y-8=0,
同理可得,BC的中垂线方程为x+y+1=0
联立两个中垂线方程,得圆心坐标为M(2,-3)
所以半径r=|AM|=
故外接圆的标准方程是(x-2)2+(y+3)2=25
A
B
C
例3 已知圆心为C的圆经过A(1,1),B(2,-2)两点,且圆心C在直线l:x-y+1=0上,求此圆的标准方程.
【代数法】: 设所求的方程是 (x-a)2+(y-b)2=r2
把点A,B的坐标代入圆得方程,圆心C(a,b)代入直线l,得
故外接圆的标准方程是(x+3)2+(y+2)2=25
例4 已知圆心为C的圆经过A(1,1),B(2,-2)两点,且圆心C在直线l:x-y+1=0上,求此圆的标准方程.
几何角度:如何确定圆心呢?
x
O
A(1,1)
B(2,-2)
y
圆心
在l上
在AB中垂线上
AB中点
AB斜率
【几何法】: (AB的中垂线与l的交点即为圆心)
因为A(1,1),B(2,-2)
所以AB的中点坐标为(,-),且kAB=-3
所以AB中垂线的斜率为,
则AB中垂线方程为y+=(x-),即x-3y-3=0,
联立中垂线方程与直线l: x-y+1=0,得圆心坐标为M(-3,-2)
所以半径r=|AC|=
故外接圆的标准方程是(x+3)2+(y+2)2=25
x
O
A(1,1)
B(2,-2)
y
通过本节课,你学到了哪些知识?
