海南省定安县2023-2024学年高二上学期开学考试数学试题(PDF版含答案)
文档属性
| 名称 | 海南省定安县2023-2024学年高二上学期开学考试数学试题(PDF版含答案) |

|
|
| 格式 | |||
| 文件大小 | 1.2MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教A版(2019) | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-09-12 00:00:00 | ||
图片预览


文档简介
2022级高二第一期学期开学考
数学
一、选择题(每小题 5 分,共 40 分)
1. 集合 A {1,2,3,4}, B {3,4,5,6} ,则 A B ( )
A.{1,2,3,45,6} B.{3,4} C.{1,2,3,4,5} D.{2,3,4,5,6}
2 i
2. 复数 在复平面所对应的点所在的象限为( )
1 3i
A.第一象限 B.第二象限 C.第三象限 D.第四象限
3. 在正六边形 ABCDEF 中, BA CD EF ( )
A.0 B.BE C.AD D.CF
4. 已知向量 a (2,4),b ( 1,1),则 2a b ( )
A.(5,7) B.(5,9) C.(3,7) D.(3,9)
5. 已知向量 a,b满足 a 1,b 3, a 2b 3,则 a b ( )
A. 2 B. 1 C.1 D.2
6. 在 ABC中,角 A,B,C的对边分别为 a,b,c, a 8 3,b 6, A 600 ,则 sin B
( )
A. 2 B. 6 C. 2 D. 3
3 3 2 8
7.某市为了解高中教师对新冠肺炎防控知识的掌握情况,调研组采用分层抽样的
方法,从甲、乙、丙三所高中共抽取 60 名教师进行调查。已知三所学校分别有
180名,270名,90名教师,则从乙校中应抽取的人数为( )
A.10 B.20 C.30 D.40
8.从 1,2,3,4 这四个数中一次随机地取两个数,则其中一个数是另一个数的
两倍的概率是( B )
A. 1 B. 1 C. 1 D. 1
6 3 9 2
二、多项选择题(每题均有多个选项正确,每题 5 分,没有选全对 2 分,选错 0
分,共计 20分)
9.已知 , , 是三个不重合的平面, l是直线,给出的下列命题中,正确的命
题有( )
A.若 l上两点到 的距离相等,则 l // B.若 l ,l // ,则
- 1 -
{#{QQABSYaQggAIAAAAARgCUQESCkAQkBACCAgOxBAMoAABCBFABAA=}#}
C.若 // ,l ,且 l // ,则 l // D.若 // , // ,则 //
2
10.下列关于复数 z 的四个命题,其中真命题为( )
1 i
A. z 2 B. z 2 2i C. 的共轭复数为 1 i D. z的虚部为 1
11.口袋里装有 1 红,2 白,3 黄共 6 个形状大小完全相同的小球,从中任取 2 球,
事件 A=取出的两球同色,B=取出的 2 球中至少有一个黄球,C=取出的 2 球中至
少有一个白球,D=取出两个球不同色。下列判断中正确的是( )
A.事件 A 与 D 为对立事件 B.事件 B 与 C是互斥事件
C.事件 C 与 E为对立事件 D.事件 P(C E) 1
12.下列统计量中,能度量样本 x1, x2 , x3...xn的离散程度的是( )
A.样本 x1, x2 , x3...xn的标准差 B.样本 x1, x2 , x3...xn的中位数
C.样本 x1, x2 , x3...xn的极差 D.样本 x1, x2 , x3...xn的平均数
三、填空题(每小题 5分,共 20 分)
13.已知向量 a (1,3),b (3,4),若 a b b,则 。
14.在 ABC 中 , 角 A,B,C 的 对 边 分 别 为 a,b,c , 若 ABC 的 面 积 为
3(a2 b2 c2 )
,则 A= 。
4
15. i 9 2i是虚数单位,复数 = 。
2 i
16.如图,在长方体 ABCD A1B1C1D1中, AB BC 2,AA1 1 ,则 AC1 与平面
A1B1C1D1所成角的正弦值为 。
四、解答题(第 17题 10分,第 18,19,20,21,22题 12 分,共计 70分)
17.在① (sin B sinC)2 sin 2 A sin BsinC b sin B C ;② a sin B ;
2
③ a sin B b cos(A )这三个条件中任选一个,补充在下面问题中并作答。
6
- 2 -
{#{QQABSYaQggAIAAAAARgCUQESCkAQkBACCAgOxBAMoAABCBFABAA=}#}
问题: ABC中,角 A,B,C的对边分别为 a,b,c,若 2a b c, ,求
角 A和 B。
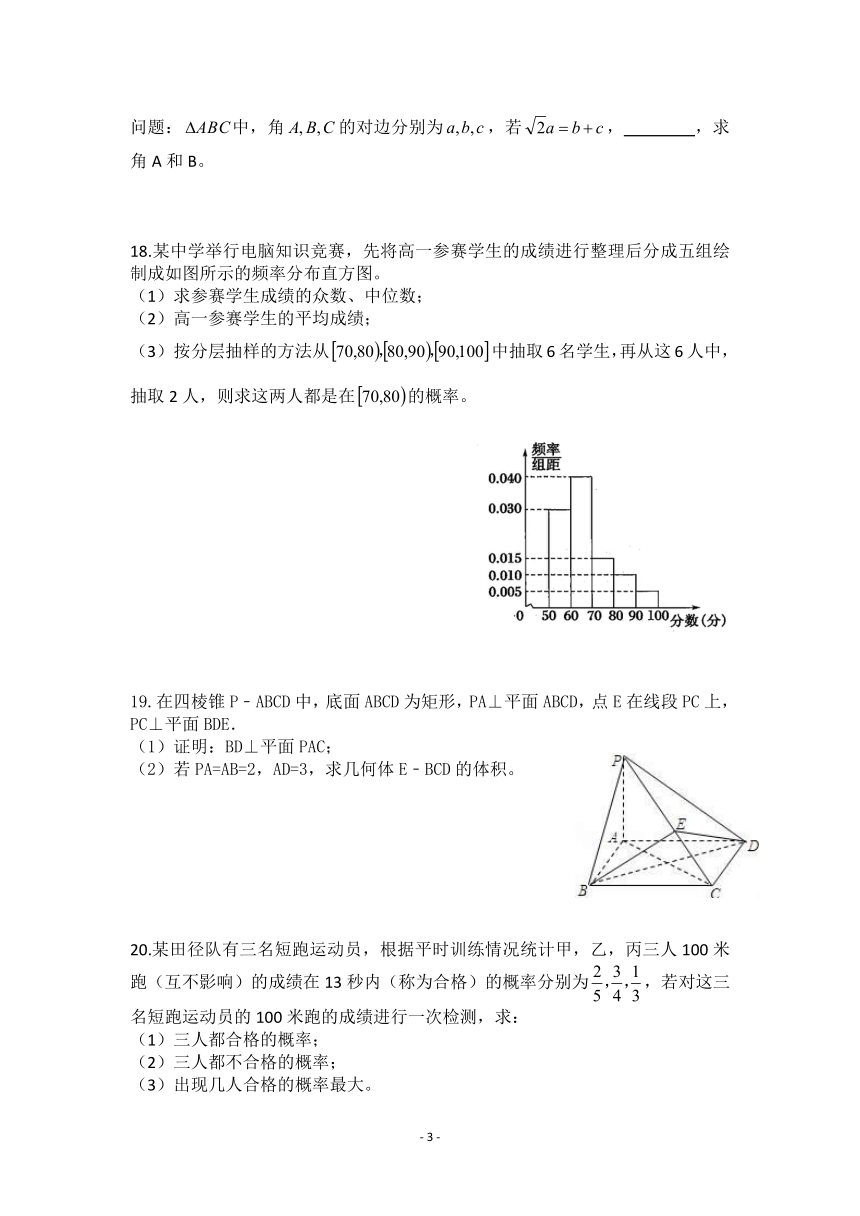
18.某中学举行电脑知识竞赛,先将高一参赛学生的成绩进行整理后分成五组绘
制成如图所示的频率分布直方图。
(1)求参赛学生成绩的众数、中位数;
(2)高一参赛学生的平均成绩;
(3)按分层抽样的方法从 70,80 , 80,90 , 90,100 中抽取 6名学生,再从这 6人中,
抽取 2人,则求这两人都是在 70,80 的概率。
19.在四棱锥 P﹣ABCD 中,底面 ABCD 为矩形,PA⊥平面 ABCD,点 E在线段 PC 上,
PC⊥平面 BDE.
(1)证明:BD⊥平面 PAC;
(2)若 PA=AB=2,AD=3,求几何体 E﹣BCD 的体积。
20.某田径队有三名短跑运动员,根据平时训练情况统计甲,乙,丙三人 100 米
2 3 1
跑(互不影响)的成绩在 13 秒内(称为合格)的概率分别为 ,,,若对这三
5 4 3
名短跑运动员的 100米跑的成绩进行一次检测,求:
(1)三人都合格的概率;
(2)三人都不合格的概率;
(3)出现几人合格的概率最大。
- 3 -
{#{QQABSYaQggAIAAAAARgCUQESCkAQkBACCAgOxBAMoAABCBFABAA=}#}
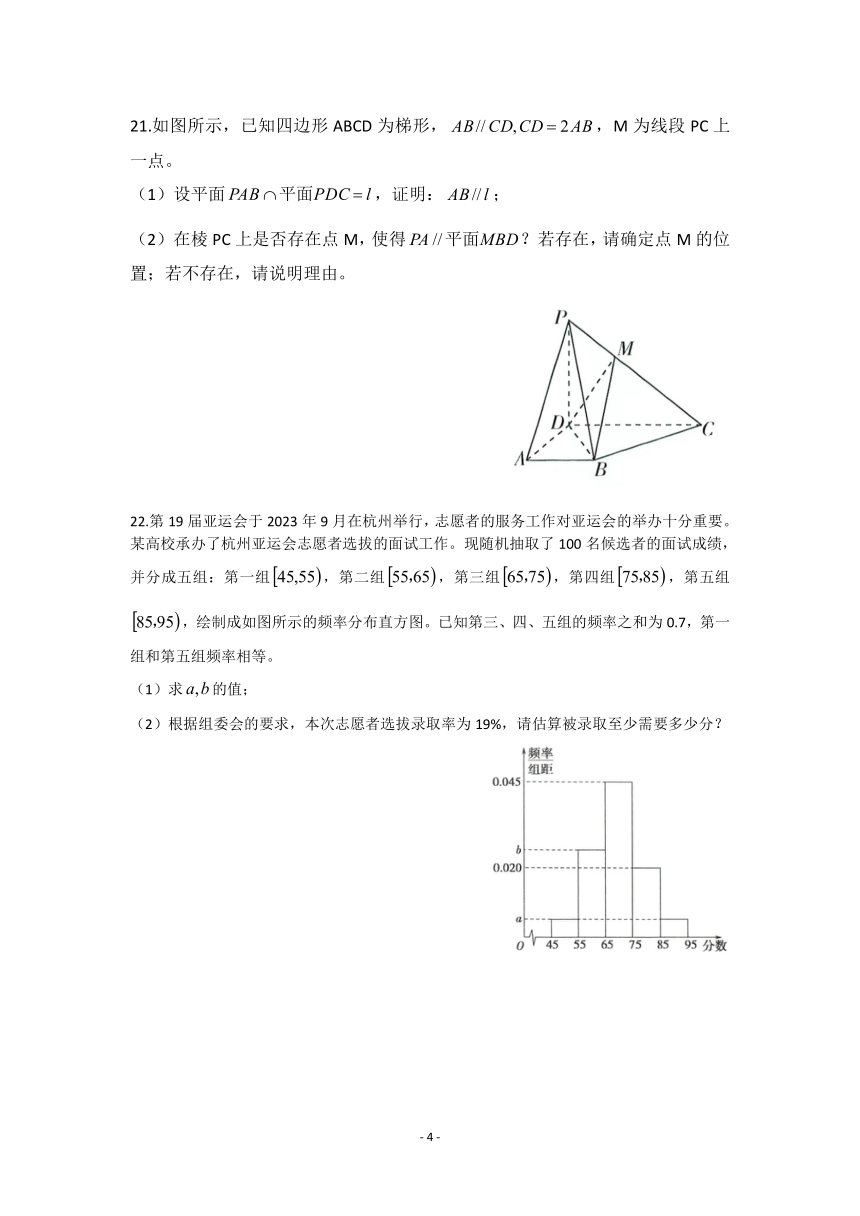
21.如图所示,已知四边形 ABCD 为梯形, AB //CD,CD 2AB,M 为线段 PC 上
一点。
(1)设平面 PAB 平面PDC l,证明: AB // l;
(2)在棱 PC 上是否存在点 M,使得 PA //平面MBD?若存在,请确定点 M的位
置;若不存在,请说明理由。
22.第 19 届亚运会于 2023 年 9 月在杭州举行,志愿者的服务工作对亚运会的举办十分重要。
某高校承办了杭州亚运会志愿者选拔的面试工作。现随机抽取了 100 名候选者的面试成绩,
并分成五组:第一组 45,55 ,第二组 55,65 ,第三组 65,75 ,第四组 75,85 ,第五组
85,95 ,绘制成如图所示的频率分布直方图。已知第三、四、五组的频率之和为 0.7,第一
组和第五组频率相等。
(1)求 a,b的值;
(2)根据组委会的要求,本次志愿者选拔录取率为 19%,请估算被录取至少需要多少分?
- 4 -
{#{QQABSYaQggAIAAAAARgCUQESCkAQkBACCAgOxBAMoAABCBFABAA=}#}
答案解析
一、单项选择题:
1 2 3 4 5 6 7 8
B A D D C D C B
二、多项选择题:
9 10 11 12
BCD BD AD AC
三、填空题:
3 2
13. ; 14. ; 15.4 i 1; 16. ;
5 3 3
四、解答题:
17.
- 5 -
{#{QQABSYaQggAIAAAAARgCUQESCkAQkBACCAgOxBAMoAABCBFABAA=}#}
18.解: 50,60 的频率为0.03 10 0.3; 60,70 的频率为0.04 10 0.4;
70,80 的频率为0.015 10 0.15; 80,90 的频率为0.01 10 0.1;
90,100 的频率为0.005 10 0.05;
(1)由题图可知众数为 65,因为第一个小矩形的面积为 0.3,所以设中位数为
60 x,则0.3 x 0.04 0.5,解得 x 5,所以中位数为 60+5=65.
(2)依题意,平均成绩为55 0.3 65 0.4 75 0.15 85 0.1 95 0.05 67。
所以平均成绩为 67.
(3)按分层抽样的方法从 70,80 , 80,90 , 90,100 中抽取 6 名学生,则分别抽取了
- 6 -
{#{QQABSYaQggAIAAAAARgCUQESCkAQkBACCAgOxBAMoAABCBFABAA=}#}
3 人,2 人,1 人。设这 6 人分别为 A,B,C,D,E,F。再从其中抽取 2 人,这一共有
AB,AC,AD,AE,AF,BC,BD,BE,BF,CD,CE,CF,DE,DF,EF,总共 15 种情况。两人都在 70,80 有
CD 一种情况,则求这两人都是在 70,80 1的概率为 。
15
19.(1)∵ PA 平面ABCD,∴ PA BD,∵ PC 平面BDE,∴ PC BD。
又 PC PA P,∴BD⊥平面 PAC。故得证。
(2)如图,设 AC与BD的交点为 O,连接 OE。
∵ PC 平面BDE,∴ PC OE。由(1)可知,BD⊥平面 PAC,∴BD⊥AC。
由题可知,四边形 ABCD 为正方形。由 AD=2,得 AC=BD= 2 2,OC= 2。
在 Rt ABC中,PC PA 2 AC2 3。易知 Rt PAC ∽ Rt OEC,
OE CE OC OE CE 2 2
所以 ,即 ,∴OE ,CE 4 .
PA AC PC 1 2 2 3 3 3
V 1 S BD 1 1 1 2 4 8∴ E BCD CED OE CE BD 2 2 .3 3 2 6 3 3 27
8
综上所述,几何体 E﹣BCD 的体积是 。
27
- 7 -
{#{QQABSYaQggAIAAAAARgCUQESCkAQkBACCAgOxBAMoAABCBFABAA=}#}
- 8 -
{#{QQABSYaQggAIAAAAARgCUQESCkAQkBACCAgOxBAMoAABCBFABAA=}#}
- 9 -
{#{QQABSYaQggAIAAAAARgCUQESCkAQkBACCAgOxBAMoAABCBFABAA=}#}
数学
一、选择题(每小题 5 分,共 40 分)
1. 集合 A {1,2,3,4}, B {3,4,5,6} ,则 A B ( )
A.{1,2,3,45,6} B.{3,4} C.{1,2,3,4,5} D.{2,3,4,5,6}
2 i
2. 复数 在复平面所对应的点所在的象限为( )
1 3i
A.第一象限 B.第二象限 C.第三象限 D.第四象限
3. 在正六边形 ABCDEF 中, BA CD EF ( )
A.0 B.BE C.AD D.CF
4. 已知向量 a (2,4),b ( 1,1),则 2a b ( )
A.(5,7) B.(5,9) C.(3,7) D.(3,9)
5. 已知向量 a,b满足 a 1,b 3, a 2b 3,则 a b ( )
A. 2 B. 1 C.1 D.2
6. 在 ABC中,角 A,B,C的对边分别为 a,b,c, a 8 3,b 6, A 600 ,则 sin B
( )
A. 2 B. 6 C. 2 D. 3
3 3 2 8
7.某市为了解高中教师对新冠肺炎防控知识的掌握情况,调研组采用分层抽样的
方法,从甲、乙、丙三所高中共抽取 60 名教师进行调查。已知三所学校分别有
180名,270名,90名教师,则从乙校中应抽取的人数为( )
A.10 B.20 C.30 D.40
8.从 1,2,3,4 这四个数中一次随机地取两个数,则其中一个数是另一个数的
两倍的概率是( B )
A. 1 B. 1 C. 1 D. 1
6 3 9 2
二、多项选择题(每题均有多个选项正确,每题 5 分,没有选全对 2 分,选错 0
分,共计 20分)
9.已知 , , 是三个不重合的平面, l是直线,给出的下列命题中,正确的命
题有( )
A.若 l上两点到 的距离相等,则 l // B.若 l ,l // ,则
- 1 -
{#{QQABSYaQggAIAAAAARgCUQESCkAQkBACCAgOxBAMoAABCBFABAA=}#}
C.若 // ,l ,且 l // ,则 l // D.若 // , // ,则 //
2
10.下列关于复数 z 的四个命题,其中真命题为( )
1 i
A. z 2 B. z 2 2i C. 的共轭复数为 1 i D. z的虚部为 1
11.口袋里装有 1 红,2 白,3 黄共 6 个形状大小完全相同的小球,从中任取 2 球,
事件 A=取出的两球同色,B=取出的 2 球中至少有一个黄球,C=取出的 2 球中至
少有一个白球,D=取出两个球不同色。下列判断中正确的是( )
A.事件 A 与 D 为对立事件 B.事件 B 与 C是互斥事件
C.事件 C 与 E为对立事件 D.事件 P(C E) 1
12.下列统计量中,能度量样本 x1, x2 , x3...xn的离散程度的是( )
A.样本 x1, x2 , x3...xn的标准差 B.样本 x1, x2 , x3...xn的中位数
C.样本 x1, x2 , x3...xn的极差 D.样本 x1, x2 , x3...xn的平均数
三、填空题(每小题 5分,共 20 分)
13.已知向量 a (1,3),b (3,4),若 a b b,则 。
14.在 ABC 中 , 角 A,B,C 的 对 边 分 别 为 a,b,c , 若 ABC 的 面 积 为
3(a2 b2 c2 )
,则 A= 。
4
15. i 9 2i是虚数单位,复数 = 。
2 i
16.如图,在长方体 ABCD A1B1C1D1中, AB BC 2,AA1 1 ,则 AC1 与平面
A1B1C1D1所成角的正弦值为 。
四、解答题(第 17题 10分,第 18,19,20,21,22题 12 分,共计 70分)
17.在① (sin B sinC)2 sin 2 A sin BsinC b sin B C ;② a sin B ;
2
③ a sin B b cos(A )这三个条件中任选一个,补充在下面问题中并作答。
6
- 2 -
{#{QQABSYaQggAIAAAAARgCUQESCkAQkBACCAgOxBAMoAABCBFABAA=}#}
问题: ABC中,角 A,B,C的对边分别为 a,b,c,若 2a b c, ,求
角 A和 B。
18.某中学举行电脑知识竞赛,先将高一参赛学生的成绩进行整理后分成五组绘
制成如图所示的频率分布直方图。
(1)求参赛学生成绩的众数、中位数;
(2)高一参赛学生的平均成绩;
(3)按分层抽样的方法从 70,80 , 80,90 , 90,100 中抽取 6名学生,再从这 6人中,
抽取 2人,则求这两人都是在 70,80 的概率。
19.在四棱锥 P﹣ABCD 中,底面 ABCD 为矩形,PA⊥平面 ABCD,点 E在线段 PC 上,
PC⊥平面 BDE.
(1)证明:BD⊥平面 PAC;
(2)若 PA=AB=2,AD=3,求几何体 E﹣BCD 的体积。
20.某田径队有三名短跑运动员,根据平时训练情况统计甲,乙,丙三人 100 米
2 3 1
跑(互不影响)的成绩在 13 秒内(称为合格)的概率分别为 ,,,若对这三
5 4 3
名短跑运动员的 100米跑的成绩进行一次检测,求:
(1)三人都合格的概率;
(2)三人都不合格的概率;
(3)出现几人合格的概率最大。
- 3 -
{#{QQABSYaQggAIAAAAARgCUQESCkAQkBACCAgOxBAMoAABCBFABAA=}#}
21.如图所示,已知四边形 ABCD 为梯形, AB //CD,CD 2AB,M 为线段 PC 上
一点。
(1)设平面 PAB 平面PDC l,证明: AB // l;
(2)在棱 PC 上是否存在点 M,使得 PA //平面MBD?若存在,请确定点 M的位
置;若不存在,请说明理由。
22.第 19 届亚运会于 2023 年 9 月在杭州举行,志愿者的服务工作对亚运会的举办十分重要。
某高校承办了杭州亚运会志愿者选拔的面试工作。现随机抽取了 100 名候选者的面试成绩,
并分成五组:第一组 45,55 ,第二组 55,65 ,第三组 65,75 ,第四组 75,85 ,第五组
85,95 ,绘制成如图所示的频率分布直方图。已知第三、四、五组的频率之和为 0.7,第一
组和第五组频率相等。
(1)求 a,b的值;
(2)根据组委会的要求,本次志愿者选拔录取率为 19%,请估算被录取至少需要多少分?
- 4 -
{#{QQABSYaQggAIAAAAARgCUQESCkAQkBACCAgOxBAMoAABCBFABAA=}#}
答案解析
一、单项选择题:
1 2 3 4 5 6 7 8
B A D D C D C B
二、多项选择题:
9 10 11 12
BCD BD AD AC
三、填空题:
3 2
13. ; 14. ; 15.4 i 1; 16. ;
5 3 3
四、解答题:
17.
- 5 -
{#{QQABSYaQggAIAAAAARgCUQESCkAQkBACCAgOxBAMoAABCBFABAA=}#}
18.解: 50,60 的频率为0.03 10 0.3; 60,70 的频率为0.04 10 0.4;
70,80 的频率为0.015 10 0.15; 80,90 的频率为0.01 10 0.1;
90,100 的频率为0.005 10 0.05;
(1)由题图可知众数为 65,因为第一个小矩形的面积为 0.3,所以设中位数为
60 x,则0.3 x 0.04 0.5,解得 x 5,所以中位数为 60+5=65.
(2)依题意,平均成绩为55 0.3 65 0.4 75 0.15 85 0.1 95 0.05 67。
所以平均成绩为 67.
(3)按分层抽样的方法从 70,80 , 80,90 , 90,100 中抽取 6 名学生,则分别抽取了
- 6 -
{#{QQABSYaQggAIAAAAARgCUQESCkAQkBACCAgOxBAMoAABCBFABAA=}#}
3 人,2 人,1 人。设这 6 人分别为 A,B,C,D,E,F。再从其中抽取 2 人,这一共有
AB,AC,AD,AE,AF,BC,BD,BE,BF,CD,CE,CF,DE,DF,EF,总共 15 种情况。两人都在 70,80 有
CD 一种情况,则求这两人都是在 70,80 1的概率为 。
15
19.(1)∵ PA 平面ABCD,∴ PA BD,∵ PC 平面BDE,∴ PC BD。
又 PC PA P,∴BD⊥平面 PAC。故得证。
(2)如图,设 AC与BD的交点为 O,连接 OE。
∵ PC 平面BDE,∴ PC OE。由(1)可知,BD⊥平面 PAC,∴BD⊥AC。
由题可知,四边形 ABCD 为正方形。由 AD=2,得 AC=BD= 2 2,OC= 2。
在 Rt ABC中,PC PA 2 AC2 3。易知 Rt PAC ∽ Rt OEC,
OE CE OC OE CE 2 2
所以 ,即 ,∴OE ,CE 4 .
PA AC PC 1 2 2 3 3 3
V 1 S BD 1 1 1 2 4 8∴ E BCD CED OE CE BD 2 2 .3 3 2 6 3 3 27
8
综上所述,几何体 E﹣BCD 的体积是 。
27
- 7 -
{#{QQABSYaQggAIAAAAARgCUQESCkAQkBACCAgOxBAMoAABCBFABAA=}#}
- 8 -
{#{QQABSYaQggAIAAAAARgCUQESCkAQkBACCAgOxBAMoAABCBFABAA=}#}
- 9 -
{#{QQABSYaQggAIAAAAARgCUQESCkAQkBACCAgOxBAMoAABCBFABAA=}#}
同课章节目录
