【同步作业】人教版七(上)2.2 整式的加减 基础夯实专题 整式的加减与求值 (课件版)
文档属性
| 名称 | 【同步作业】人教版七(上)2.2 整式的加减 基础夯实专题 整式的加减与求值 (课件版) |

|
|
| 格式 | pptx | ||
| 文件大小 | 681.5KB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-09-12 14:59:38 | ||
图片预览


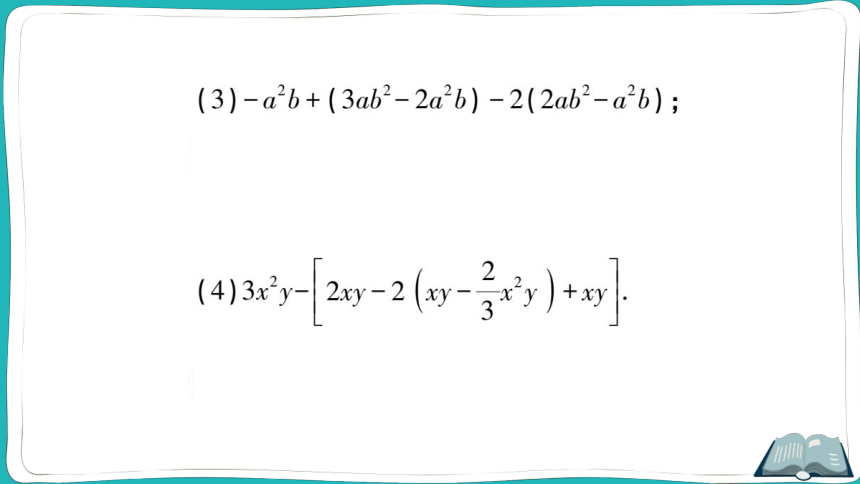

文档简介
(共9张PPT)
类型一
整式的加减
1.计算:
(1)4b-3b-2b2+4b;
解:原式=2b+b;
(2)2(2ab+3a)-3(2a-ab);
解:原式=7ab;
(3)-a2b+(3ab2-2a2b)-2(2ab2-a2b);
解:原式=-ab-ab2;
432-2子*w
5
解:原式=。xy-y
3
2.已知式子A=-6x2y+4xy2-2x-5,B=-3x2y+
2xy2-x+2y-3.求:
(1)2A+B;
(2)A-2B.
解:(1)2A+B=2(-6x2y+4xy-2x-5)+(-3xy+
2xy2-x+2y-3)
=-15xy+10xy2-5x+2y-13;
(2)A-2B=(-6x2y+4xy2-2x-5)-2(-3x2y+
2xy2-x+2y-3)
=-4y+1.
类型二
整式的化简求值
3.[西安临潼区期中]先化简,再求值:2(x2+4x)-
(2x2+5x-4),其中x=-1.
解:原式=2x2+8x-2x2-5x+4=3x+4.
当x=-1时,原式=3×(-1)+4=1.
4.先化简,再求值:6(2a2b-ab2)-3(-ab+4ab),
其中a,b的值满足a-2+(b+3)2=0.
解:原式=12a2b-6ab2+3ab2-12a2b=-3ab2
因为a-2+(b+3)2=0,
所以a-2=0,b+3=0,则a=2,b=-3.
当a=2,b=-3时,原式=-3×2×(-3)2=-54.
5.先化简,再求值:-2y3+(3xy2-x2y)-2(xy2-
y),其中x是最大的负整数,y是倒数等于它
本身的自然数.
解:原式=-2y3+3xy2-x2y-2xy2+2y3=xy2-2y.
由题意知x=-1,y=1.
当x=-1,y=1时,原式=-1×12-(-1)2×1=-2
6.[南充期末]先化简,再求值:
2
2
mn
[名m+3a-j+3n,其中m-
3
2
1
2
解:原式m-(名m24m-)+3
5
4
mn-
mn2-3mn+m+3mn=
2+m.
mn
2
6
3
3
当
m=
时,原式=×x()广+=2
7.己知xy=2,x+y=3,求5x+(3xy+10y)-(2xy+
2y-3x)的值.
解:原式=5x+3xy+10y-2xy-2y+3x=xy+8x+8y
=xy+8(x+y).
当xy=2,x+y=3时,原式=2+8×3=26.
类型一
整式的加减
1.计算:
(1)4b-3b-2b2+4b;
解:原式=2b+b;
(2)2(2ab+3a)-3(2a-ab);
解:原式=7ab;
(3)-a2b+(3ab2-2a2b)-2(2ab2-a2b);
解:原式=-ab-ab2;
432-2子*w
5
解:原式=。xy-y
3
2.已知式子A=-6x2y+4xy2-2x-5,B=-3x2y+
2xy2-x+2y-3.求:
(1)2A+B;
(2)A-2B.
解:(1)2A+B=2(-6x2y+4xy-2x-5)+(-3xy+
2xy2-x+2y-3)
=-15xy+10xy2-5x+2y-13;
(2)A-2B=(-6x2y+4xy2-2x-5)-2(-3x2y+
2xy2-x+2y-3)
=-4y+1.
类型二
整式的化简求值
3.[西安临潼区期中]先化简,再求值:2(x2+4x)-
(2x2+5x-4),其中x=-1.
解:原式=2x2+8x-2x2-5x+4=3x+4.
当x=-1时,原式=3×(-1)+4=1.
4.先化简,再求值:6(2a2b-ab2)-3(-ab+4ab),
其中a,b的值满足a-2+(b+3)2=0.
解:原式=12a2b-6ab2+3ab2-12a2b=-3ab2
因为a-2+(b+3)2=0,
所以a-2=0,b+3=0,则a=2,b=-3.
当a=2,b=-3时,原式=-3×2×(-3)2=-54.
5.先化简,再求值:-2y3+(3xy2-x2y)-2(xy2-
y),其中x是最大的负整数,y是倒数等于它
本身的自然数.
解:原式=-2y3+3xy2-x2y-2xy2+2y3=xy2-2y.
由题意知x=-1,y=1.
当x=-1,y=1时,原式=-1×12-(-1)2×1=-2
6.[南充期末]先化简,再求值:
2
2
mn
[名m+3a-j+3n,其中m-
3
2
1
2
解:原式m-(名m24m-)+3
5
4
mn-
mn2-3mn+m+3mn=
2+m.
mn
2
6
3
3
当
m=
时,原式=×x()广+=2
7.己知xy=2,x+y=3,求5x+(3xy+10y)-(2xy+
2y-3x)的值.
解:原式=5x+3xy+10y-2xy-2y+3x=xy+8x+8y
=xy+8(x+y).
当xy=2,x+y=3时,原式=2+8×3=26.
