数学人教A版(2019)选择性必修第一册2.2.1直线的点斜式方程(共20张ppt)
文档属性
| 名称 | 数学人教A版(2019)选择性必修第一册2.2.1直线的点斜式方程(共20张ppt) |  | |
| 格式 | pptx | ||
| 文件大小 | 927.5KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教A版(2019) | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-09-12 15:53:45 | ||
图片预览




文档简介
(共20张PPT)
2.2.1直线的点斜式方程
1.掌握直线方程的点斜式和斜截式,并会用它们求直线的方程
2.了解直线的斜截式方程与一次函数的关系
3.会用直线的点斜式方程与斜截式方程解决直线的平行与垂直问题.
学习目标
笛卡尔出生于法国,毕业于普瓦捷大学,法国著名哲学家、物理学家、数学家,被黑格尔称为“近代哲学之父”。
在笛卡尔之前,几何与代数是数学中两个不同的研究领域。他站在方法论的自然哲学的高度,认为希腊人的几何学过于依赖于图形,束缚了人的想象力。对于当时流行的代数学,他觉得它完全从属于法则和公式,不能成为一门改进智力的科学。因此他提出必须把几何与代数的优点结合起来,建立一种“真正的数学”。
笛卡尔的思想核心是:把几何学的问题归结成代数形式的问题,用代数学的方法进行计算、证明,从而达到最终解决几何问题的目的。依照这种思想他创立了“解析几何学”。
情景引入
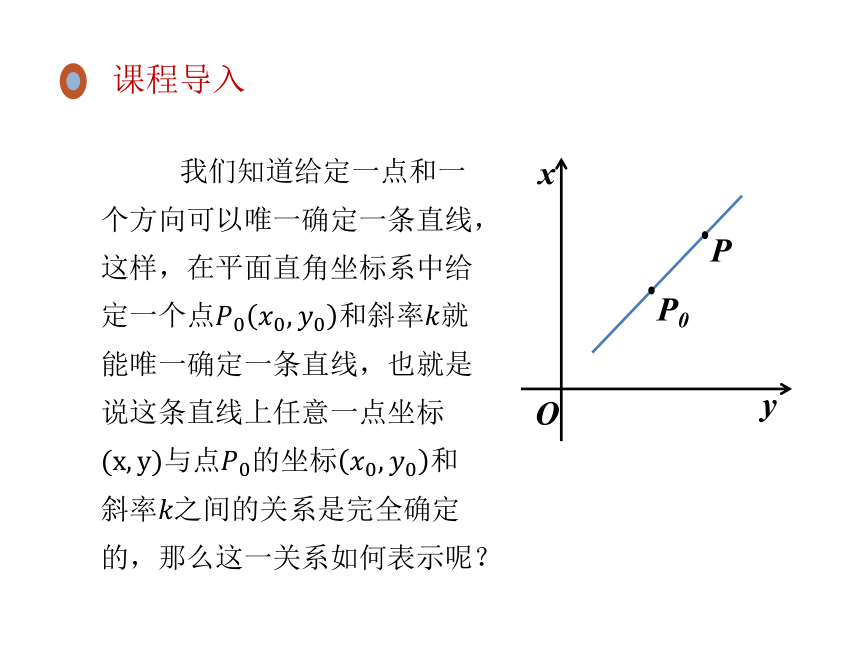
我们知道给定一点和一个方向可以唯一确定一条直线,这样,在平面直角坐标系中给定一个点和斜率就能唯一确定一条直线,也就是说这条直线上任意一点坐标与点坐标和斜率之间的关系是完全确定的,那么这一关系如何表示呢?
课程导入
x
O
y
P0
P
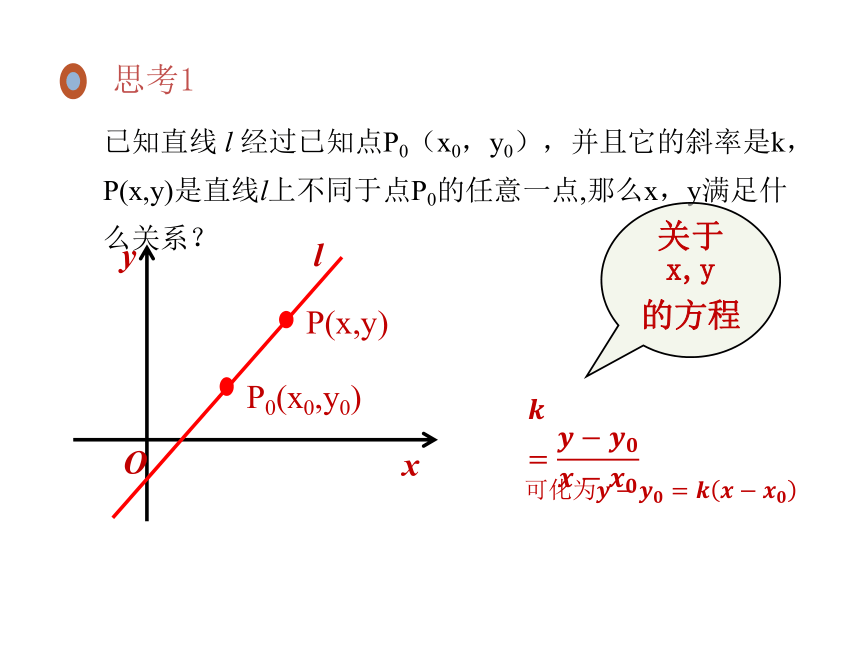
已知直线 l 经过已知点P0(x0,y0),并且它的斜率是k,P(x,y)是直线l上不同于点P0的任意一点,那么x,y满足什么关系?
x
y
O
P(x,y)
l
P0(x0,y0)
关于x,y
的方程
思考1
满足方程y-y0=k(x-x0)的所有点P(x,y)是否都在直线l上 为什么?
思考2
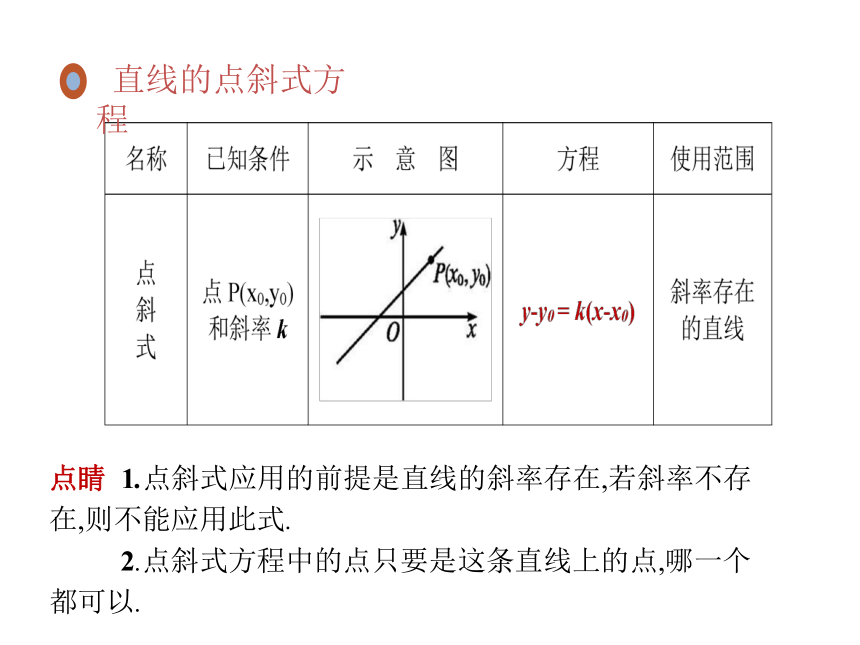
点睛 1.点斜式应用的前提是直线的斜率存在,若斜率不存在,则不能应用此式.
2.点斜式方程中的点只要是这条直线上的点,哪一个都可以.
直线的点斜式方程
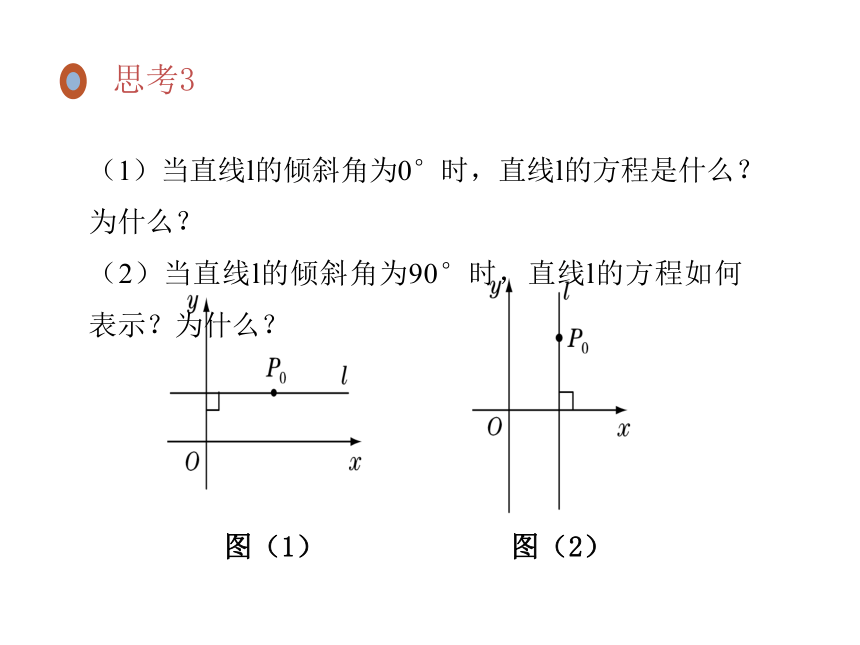
(1)当直线l的倾斜角为0°时,直线l的方程是什么?为什么?
(2)当直线l的倾斜角为90°时,直线l的方程如何表示?为什么?
图(1)
图(2)
思考3
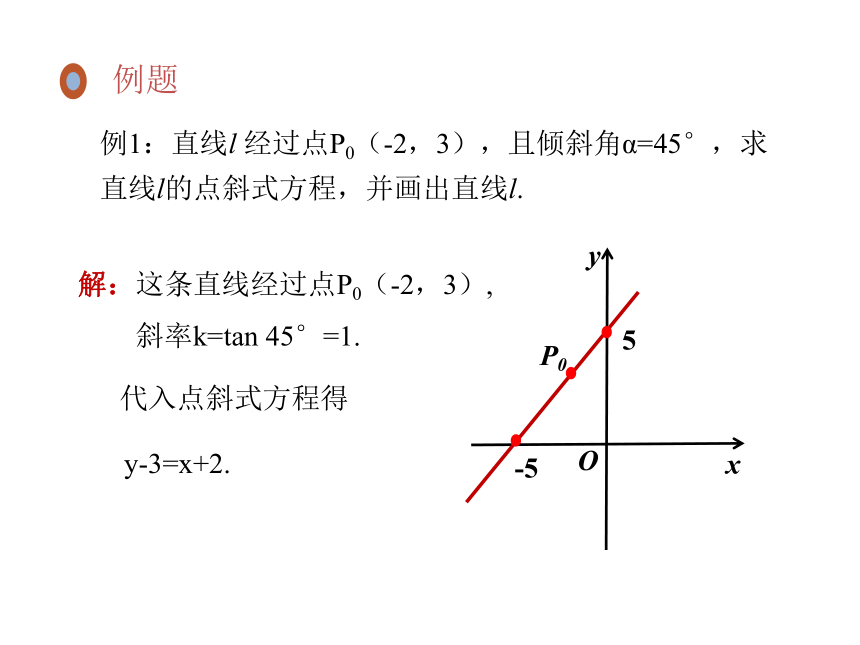
例1:直线l 经过点P0(-2,3),且倾斜角α=45°,求直线l的点斜式方程,并画出直线l.
解:这条直线经过点P0(-2,3),
斜率k=tan 45°=1.
代入点斜式方程得
y-3=x+2.
O
x
y
P0
5
-5
例题
1、求满足下列条件的直线方程:
(1)经过点(2,-3),倾斜角是直线 y=x 倾斜角的2倍;
(2)经过点P(5,-2),且与y轴平行;
(3)过P(-2,3),Q(5,-4)两点.
思路分析:先求出直线的斜率,然后由点斜式写出方程.
阶段检测(一)
(2)与y轴平行的直线,其斜率k不存在,不能用点斜式方程表示.
但直线上点的横坐标均为5,
故直线方程可记为x=5.
∵直线过点P(-2,3),
∴由直线的点斜式方程可得直线方程为y-3=-(x+2),即x+y-1=0.
已知直线l的斜率是k,与y轴的交点是P(0,b),求得直线方程是什么?
代入点斜式方程得,
直线l 的方程:y-b=k(x-0),
即
O
x
y
P(0,b)
y = kx + b.
斜率
在y轴上的截距
方程y= kx+b由直线的斜率k与它在y轴上的截距b确定,所以方程叫做直线的斜截式方程,简称斜截式.
思考3
1.直线的斜截式方程是直线的点斜式方程的特殊情况.
2.截距是一个实数,它是直线与坐标轴交点的横坐标或纵坐标,可以 为正数、负数和0.当直线过原点时,它的横截距和纵截距都为0.
3.由直线的斜截式方程可直接得到直线的斜率和纵截距,如直线y=2x-1的斜率k=2,纵截距为-1.
直线的斜截式方程
点睛:
1、直线l的斜截式方程是y=-2x+3,则直线l在y轴上的截距为 .
2、一次函数的解析式y=kx+b与直线的斜截式方程y=kx+b有什么不同
一次函数的x的系数k≠0,否则就不是一次函数了;直线的斜截式方程y=kx+b中的k可以为0.
3
3、直线y=(x-)的斜率与在y轴上的截距分别是( )
A., B.,-3
C.,3 D.-,-3
【答案】B [由直线方程知直线斜率为,令x=0可得在y轴上的截距为y=-3.故选B.]
阶段检测(一)
例题
已知直线l1: y=kx+b1, l2 : y=kx+ b2,试讨论:
(1) l1∥l2的条件是什么 (2) l1⊥l2的条件是什么
分析:回忆用斜率判断两条直线平行、垂直的结论. 思考:
l1∥l2时,k1,k2,,b1,b2,有何关系
l1⊥l2时, k1,k2,,b1,b2,有何关系
点睛:根据直线的斜截式方程判断两直线平行与垂直
对于直线l1:y=k1x+b1,l2:y=k2x+b2,
l1∥l2 k1=k2,且b1≠b2;
l1⊥l2 k1k2=-1.
两直线的斜率之积为-1,则两直线一定垂直;两条直线的斜率相等,两直线不一定平行,还可能重合.
解: (1) 若l1∥l2 ,则k1=k2,此时, l1, l2与y轴的交点不同即b1 ≠ b2;
反之k1=k2 ,且b1 ≠ b2,时, l1∥l2。
(2) 若l1⊥l2 ,则k1k2 =-1; 反之k1k2 =-1时, l1⊥l2
1、 直线l1的倾斜角为135°,直线l2经过点B(-1,4).求满足下列条件的直线l2的方程.
(1)直线l2∥l1; (2)直线l2⊥l1.
解:(1)由已知直线l1的斜率k1=tan 135°=-1.
因为l2∥l1,所以直线l2的斜率k2=k1=-1.又直线l2经过点B(-1,4),
代入点斜式方程得y-4=-1×[x-(-1)],即y=-x+3.
(2)由已知直线l1的斜率k1=tan 135°=-1.
又直线l2经过点B(-1,4),
代入点斜式方程得y-4=1×[x-(-1)],即y=x+5.
阶段检测(一)
3、无论k取何值,直线y-2=k(x+1)所过的定点是 .
(-1,2)
2、已知两条直线y=ax-2和y=(2-a)x+1互相平行,则a=________.
1
课堂小结
2.2.1直线的点斜式方程
1.掌握直线方程的点斜式和斜截式,并会用它们求直线的方程
2.了解直线的斜截式方程与一次函数的关系
3.会用直线的点斜式方程与斜截式方程解决直线的平行与垂直问题.
学习目标
笛卡尔出生于法国,毕业于普瓦捷大学,法国著名哲学家、物理学家、数学家,被黑格尔称为“近代哲学之父”。
在笛卡尔之前,几何与代数是数学中两个不同的研究领域。他站在方法论的自然哲学的高度,认为希腊人的几何学过于依赖于图形,束缚了人的想象力。对于当时流行的代数学,他觉得它完全从属于法则和公式,不能成为一门改进智力的科学。因此他提出必须把几何与代数的优点结合起来,建立一种“真正的数学”。
笛卡尔的思想核心是:把几何学的问题归结成代数形式的问题,用代数学的方法进行计算、证明,从而达到最终解决几何问题的目的。依照这种思想他创立了“解析几何学”。
情景引入
我们知道给定一点和一个方向可以唯一确定一条直线,这样,在平面直角坐标系中给定一个点和斜率就能唯一确定一条直线,也就是说这条直线上任意一点坐标与点坐标和斜率之间的关系是完全确定的,那么这一关系如何表示呢?
课程导入
x
O
y
P0
P
已知直线 l 经过已知点P0(x0,y0),并且它的斜率是k,P(x,y)是直线l上不同于点P0的任意一点,那么x,y满足什么关系?
x
y
O
P(x,y)
l
P0(x0,y0)
关于x,y
的方程
思考1
满足方程y-y0=k(x-x0)的所有点P(x,y)是否都在直线l上 为什么?
思考2
点睛 1.点斜式应用的前提是直线的斜率存在,若斜率不存在,则不能应用此式.
2.点斜式方程中的点只要是这条直线上的点,哪一个都可以.
直线的点斜式方程
(1)当直线l的倾斜角为0°时,直线l的方程是什么?为什么?
(2)当直线l的倾斜角为90°时,直线l的方程如何表示?为什么?
图(1)
图(2)
思考3
例1:直线l 经过点P0(-2,3),且倾斜角α=45°,求直线l的点斜式方程,并画出直线l.
解:这条直线经过点P0(-2,3),
斜率k=tan 45°=1.
代入点斜式方程得
y-3=x+2.
O
x
y
P0
5
-5
例题
1、求满足下列条件的直线方程:
(1)经过点(2,-3),倾斜角是直线 y=x 倾斜角的2倍;
(2)经过点P(5,-2),且与y轴平行;
(3)过P(-2,3),Q(5,-4)两点.
思路分析:先求出直线的斜率,然后由点斜式写出方程.
阶段检测(一)
(2)与y轴平行的直线,其斜率k不存在,不能用点斜式方程表示.
但直线上点的横坐标均为5,
故直线方程可记为x=5.
∵直线过点P(-2,3),
∴由直线的点斜式方程可得直线方程为y-3=-(x+2),即x+y-1=0.
已知直线l的斜率是k,与y轴的交点是P(0,b),求得直线方程是什么?
代入点斜式方程得,
直线l 的方程:y-b=k(x-0),
即
O
x
y
P(0,b)
y = kx + b.
斜率
在y轴上的截距
方程y= kx+b由直线的斜率k与它在y轴上的截距b确定,所以方程叫做直线的斜截式方程,简称斜截式.
思考3
1.直线的斜截式方程是直线的点斜式方程的特殊情况.
2.截距是一个实数,它是直线与坐标轴交点的横坐标或纵坐标,可以 为正数、负数和0.当直线过原点时,它的横截距和纵截距都为0.
3.由直线的斜截式方程可直接得到直线的斜率和纵截距,如直线y=2x-1的斜率k=2,纵截距为-1.
直线的斜截式方程
点睛:
1、直线l的斜截式方程是y=-2x+3,则直线l在y轴上的截距为 .
2、一次函数的解析式y=kx+b与直线的斜截式方程y=kx+b有什么不同
一次函数的x的系数k≠0,否则就不是一次函数了;直线的斜截式方程y=kx+b中的k可以为0.
3
3、直线y=(x-)的斜率与在y轴上的截距分别是( )
A., B.,-3
C.,3 D.-,-3
【答案】B [由直线方程知直线斜率为,令x=0可得在y轴上的截距为y=-3.故选B.]
阶段检测(一)
例题
已知直线l1: y=kx+b1, l2 : y=kx+ b2,试讨论:
(1) l1∥l2的条件是什么 (2) l1⊥l2的条件是什么
分析:回忆用斜率判断两条直线平行、垂直的结论. 思考:
l1∥l2时,k1,k2,,b1,b2,有何关系
l1⊥l2时, k1,k2,,b1,b2,有何关系
点睛:根据直线的斜截式方程判断两直线平行与垂直
对于直线l1:y=k1x+b1,l2:y=k2x+b2,
l1∥l2 k1=k2,且b1≠b2;
l1⊥l2 k1k2=-1.
两直线的斜率之积为-1,则两直线一定垂直;两条直线的斜率相等,两直线不一定平行,还可能重合.
解: (1) 若l1∥l2 ,则k1=k2,此时, l1, l2与y轴的交点不同即b1 ≠ b2;
反之k1=k2 ,且b1 ≠ b2,时, l1∥l2。
(2) 若l1⊥l2 ,则k1k2 =-1; 反之k1k2 =-1时, l1⊥l2
1、 直线l1的倾斜角为135°,直线l2经过点B(-1,4).求满足下列条件的直线l2的方程.
(1)直线l2∥l1; (2)直线l2⊥l1.
解:(1)由已知直线l1的斜率k1=tan 135°=-1.
因为l2∥l1,所以直线l2的斜率k2=k1=-1.又直线l2经过点B(-1,4),
代入点斜式方程得y-4=-1×[x-(-1)],即y=-x+3.
(2)由已知直线l1的斜率k1=tan 135°=-1.
又直线l2经过点B(-1,4),
代入点斜式方程得y-4=1×[x-(-1)],即y=x+5.
阶段检测(一)
3、无论k取何值,直线y-2=k(x+1)所过的定点是 .
(-1,2)
2、已知两条直线y=ax-2和y=(2-a)x+1互相平行,则a=________.
1
课堂小结
