2023年沪科版数学八年级上册期中检测题及答案(二)(含答案)
文档属性
| 名称 | 2023年沪科版数学八年级上册期中检测题及答案(二)(含答案) |  | |
| 格式 | docx | ||
| 文件大小 | 2.5MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 沪科版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-09-13 23:51:25 | ||
图片预览


文档简介
中小学教育资源及组卷应用平台
2023年沪科版数学八年级上册期中检测题
(时间:120分钟 分值:120分)
一、选择题(每题3分,共30分)
1.如图,将三角尺的直角顶点放在直尺的一边上,∠1=30°,∠2=50°,则∠3的度数等于( )
A.50°B.30° C.20° D.15°
2. 如果在轴上,那么点的坐标是( )
A.(-2,0) B.(0,-2) C.(1,0) D.(0,1)
3.在下列条件中,①∠A+∠B=∠C; ②∠A:∠B:∠C=1:2:3; ③∠A=∠B=∠C;
④∠A=∠B=2∠C; ⑤∠A=2∠B=3∠C,能确定△ABC为直角三角形的条件有( )
A.2个 B.3个 C.4个 D.5个
4.根据下列表述,能确定具体位置是( )
A.某电影院2排 B.金寨南路 C. 北偏东 D. 东经,北纬
5.在平面直角坐标系中,点所在的象限是( )
A.第一象限 B.第二象限C.第三象限 D. 第四象限
6.等腰三角形两边长为,则第三边的长是( )
A. B. C. D.或
7.过和两点的直线一定 ( )
A.垂直于轴 B.与轴相交但不平行于轴
C.平行于轴 D.与轴、轴都不平行
8.若a、b、c为△ABC的三边长,且满足,则c的值可以为( )
A.5 B.6 C.7 D.8
9.已知一次函数与的图象在轴上相交于同一点,则的值是( )
(
第
10
题
) A. B. C. D.
10.某学校组织团员举行申奥成功宣传活动,从学校骑车出发,先上坡到达地后,宣传8分钟;然后下坡到地宣传8分钟返回,行程情况如图.若返回时,上、下坡速度仍保持不变,在A地仍要宣传8分钟,那么他们从B地返回学校用的时间是( )
A.45.2分钟 B.48分钟 C.46分钟 D.33分钟
二、填空题(每题3分,共15分)
11.平面直角坐标系中,点到轴的距离是 .
12、点P在第二象限,到x轴的距离是2,到y轴的距离是3,则P点的坐标是
13、在△ABC中,, ,则
14.点沿轴正方向平移2个单位,再沿轴负方向平移4个单位,所得到的点的坐标为__________.
15. 在平面直角坐标系中,对于点,我们把点叫做点的衍生点.已知点的衍生点为,点的衍生点为,点的衍生点为这样依次得到点若点的坐标为,若点在第四象限,则范围分别为 .
三、解答题
16.(6分)已知函数
(1)试判断点是否在这个函数的图象上,
(2)若点在这个函数图象上,求的值
17.(6分)如图,在中,,点是中边上的三分之一点,把这个三角形周长分成了和的两部分,求这个三角形的腰长和底边的长.
18. (8分)和在平面直角坐标系中的位置分别如图所示.
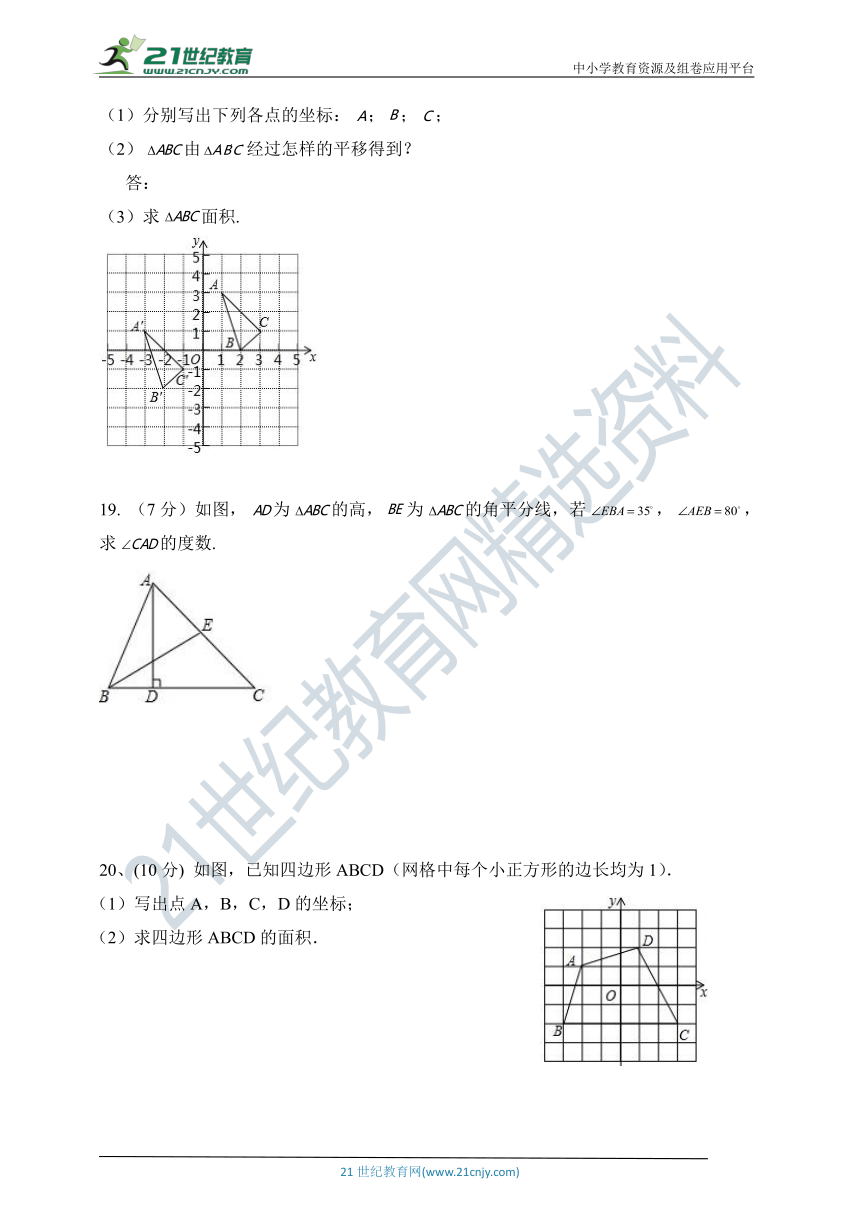
(1)分别写出下列各点的坐标:;;;
(2)由经过怎样的平移得到?
答:
(3)求面积.
19. (7分)如图,为的高,为的角平分线,若,,求的度数.
20、(10分) 如图,已知四边形ABCD(网格中每个小正方形的边长均为1).
(1)写出点A,B,C,D的坐标;
(2)求四边形ABCD的面积.
21、(10分)已知在△ABC中,∠A:∠B:∠C=2:3:4,CD是∠ACB平分线,求∠A和∠CDB的度数.
22.(12分)已知函数y=(2m+1)x+m-3.
(1)若函数图象经过原点,求m的值
(2)若函数的图象平行于直线y=3x-3,求m的值
(3)若这个函数是一次函数,且y随着x的增大而减小,求m的取值范围.
23. 附加题:(5分)
已知某种水果的批发金额与批发量的函数关系如图所示,
(1)指出金额在什么范围内,以同样的资金可以批发到较多数量的该种水果.
(2)相同的金额是多少时,可以多买水果?
参考答案
选择题
1、C 2、B 3、B 4.D 5.B 6.B 7.C 8、A 9、D 10、A
二、填空题
11. 5 12、P(-3,2) 13、50° 14、(-3,-3) 15.
三、解答题
16.(1)把代入中,得,点在一次函数上,不在函数上;
(2)在函数上,把代入中,得
17.设:,为三等分点,
, ,可得方程组,解得,
底边长为,两腰长为.
18. (1)
(2)向右平移4个单位长度,再向上平移2个单位长度(3)如图,矩形=,
,
矩形-
19.在中,,为角平分线,,
在中,,,
在中,
20、
解:(1)由图象可知A(﹣2,1),B(﹣3,﹣2),
C(3,﹣2),D(1,2); (4分)
(2)S四边形ABCD=S△ABE+S△ADF+S△CDG+S正方形AEGF
=×1×3+×1×3+×2×4+3×3=16 (10分)
21、
解:∵在△ABC中,∠A:∠B:∠C=2:3:4,
∠A+∠ACB+∠B=180°,
∴∠A=×180°=40°,∠ACB=×180°=80° (4分)
∵CD是∠ACB平分线,
∴∠ACD=ACB=40° (6分)
∴∠CDB=∠A+∠ACD=40°+40°=80° (10分)
22.
解:(1)∵y=(2m+1)x+m﹣3经过原点,是正比例函数,
∴.
解得m=3. (4分)
(2)∵函数的图象平行于直线y=3x﹣3,
∴2m+1=3,解得m=1 (8分)
(3)根据y随x的增大而减小说明k<0.即2m+1<0.
解得:m<﹣ (12分)
23.(1)
(2)设第一段函数解析式为,图像经过解得.
设第二段函数解析式,图像经过点,,,解得,,,当相同的金额是280元时,可以多买水果.
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
21世纪教育网(www.21cnjy.com)
2023年沪科版数学八年级上册期中检测题
(时间:120分钟 分值:120分)
一、选择题(每题3分,共30分)
1.如图,将三角尺的直角顶点放在直尺的一边上,∠1=30°,∠2=50°,则∠3的度数等于( )
A.50°B.30° C.20° D.15°
2. 如果在轴上,那么点的坐标是( )
A.(-2,0) B.(0,-2) C.(1,0) D.(0,1)
3.在下列条件中,①∠A+∠B=∠C; ②∠A:∠B:∠C=1:2:3; ③∠A=∠B=∠C;
④∠A=∠B=2∠C; ⑤∠A=2∠B=3∠C,能确定△ABC为直角三角形的条件有( )
A.2个 B.3个 C.4个 D.5个
4.根据下列表述,能确定具体位置是( )
A.某电影院2排 B.金寨南路 C. 北偏东 D. 东经,北纬
5.在平面直角坐标系中,点所在的象限是( )
A.第一象限 B.第二象限C.第三象限 D. 第四象限
6.等腰三角形两边长为,则第三边的长是( )
A. B. C. D.或
7.过和两点的直线一定 ( )
A.垂直于轴 B.与轴相交但不平行于轴
C.平行于轴 D.与轴、轴都不平行
8.若a、b、c为△ABC的三边长,且满足,则c的值可以为( )
A.5 B.6 C.7 D.8
9.已知一次函数与的图象在轴上相交于同一点,则的值是( )
(
第
10
题
) A. B. C. D.
10.某学校组织团员举行申奥成功宣传活动,从学校骑车出发,先上坡到达地后,宣传8分钟;然后下坡到地宣传8分钟返回,行程情况如图.若返回时,上、下坡速度仍保持不变,在A地仍要宣传8分钟,那么他们从B地返回学校用的时间是( )
A.45.2分钟 B.48分钟 C.46分钟 D.33分钟
二、填空题(每题3分,共15分)
11.平面直角坐标系中,点到轴的距离是 .
12、点P在第二象限,到x轴的距离是2,到y轴的距离是3,则P点的坐标是
13、在△ABC中,, ,则
14.点沿轴正方向平移2个单位,再沿轴负方向平移4个单位,所得到的点的坐标为__________.
15. 在平面直角坐标系中,对于点,我们把点叫做点的衍生点.已知点的衍生点为,点的衍生点为,点的衍生点为这样依次得到点若点的坐标为,若点在第四象限,则范围分别为 .
三、解答题
16.(6分)已知函数
(1)试判断点是否在这个函数的图象上,
(2)若点在这个函数图象上,求的值
17.(6分)如图,在中,,点是中边上的三分之一点,把这个三角形周长分成了和的两部分,求这个三角形的腰长和底边的长.
18. (8分)和在平面直角坐标系中的位置分别如图所示.
(1)分别写出下列各点的坐标:;;;
(2)由经过怎样的平移得到?
答:
(3)求面积.
19. (7分)如图,为的高,为的角平分线,若,,求的度数.
20、(10分) 如图,已知四边形ABCD(网格中每个小正方形的边长均为1).
(1)写出点A,B,C,D的坐标;
(2)求四边形ABCD的面积.
21、(10分)已知在△ABC中,∠A:∠B:∠C=2:3:4,CD是∠ACB平分线,求∠A和∠CDB的度数.
22.(12分)已知函数y=(2m+1)x+m-3.
(1)若函数图象经过原点,求m的值
(2)若函数的图象平行于直线y=3x-3,求m的值
(3)若这个函数是一次函数,且y随着x的增大而减小,求m的取值范围.
23. 附加题:(5分)
已知某种水果的批发金额与批发量的函数关系如图所示,
(1)指出金额在什么范围内,以同样的资金可以批发到较多数量的该种水果.
(2)相同的金额是多少时,可以多买水果?
参考答案
选择题
1、C 2、B 3、B 4.D 5.B 6.B 7.C 8、A 9、D 10、A
二、填空题
11. 5 12、P(-3,2) 13、50° 14、(-3,-3) 15.
三、解答题
16.(1)把代入中,得,点在一次函数上,不在函数上;
(2)在函数上,把代入中,得
17.设:,为三等分点,
, ,可得方程组,解得,
底边长为,两腰长为.
18. (1)
(2)向右平移4个单位长度,再向上平移2个单位长度(3)如图,矩形=,
,
矩形-
19.在中,,为角平分线,,
在中,,,
在中,
20、
解:(1)由图象可知A(﹣2,1),B(﹣3,﹣2),
C(3,﹣2),D(1,2); (4分)
(2)S四边形ABCD=S△ABE+S△ADF+S△CDG+S正方形AEGF
=×1×3+×1×3+×2×4+3×3=16 (10分)
21、
解:∵在△ABC中,∠A:∠B:∠C=2:3:4,
∠A+∠ACB+∠B=180°,
∴∠A=×180°=40°,∠ACB=×180°=80° (4分)
∵CD是∠ACB平分线,
∴∠ACD=ACB=40° (6分)
∴∠CDB=∠A+∠ACD=40°+40°=80° (10分)
22.
解:(1)∵y=(2m+1)x+m﹣3经过原点,是正比例函数,
∴.
解得m=3. (4分)
(2)∵函数的图象平行于直线y=3x﹣3,
∴2m+1=3,解得m=1 (8分)
(3)根据y随x的增大而减小说明k<0.即2m+1<0.
解得:m<﹣ (12分)
23.(1)
(2)设第一段函数解析式为,图像经过解得.
设第二段函数解析式,图像经过点,,,解得,,,当相同的金额是280元时,可以多买水果.
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
21世纪教育网(www.21cnjy.com)
同课章节目录
