2023年沪科版数学八年级上册期末测试题及答案(一)(含答案)
文档属性
| 名称 | 2023年沪科版数学八年级上册期末测试题及答案(一)(含答案) |

|
|
| 格式 | docx | ||
| 文件大小 | 1.4MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 沪科版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-09-13 00:00:00 | ||
图片预览



文档简介
中小学教育资源及组卷应用平台
2023年沪科版数学八年级上册期末测试题(一)
(时间:120分钟 分值:120分)
一、选择题(本大题共10小题,每小题4分,满分40分)
1. 点P在x轴的下方,且距离x轴3个单位长度,距离y轴4个单位长度,则点P的坐标 为( )
(4,-3) B. (3,-4)
C. (-3,-4)或(3,-4) D. (-4,-3)或(4,-3)
2. 若三条线段中,,为奇数,那么由a、b、c为边组成的三角形共有( )
A. 1个 B. 3个 C. 无数多个 D. 无法确定
3. 在同一直角坐标系中,若直线与直线平行,则( )
A., B., C., D.,
4.在以下节水、回收、节能、绿色食品四个标志中,是轴对称图形的是
5.已知非等腰三角形的两边长分别是2 cm和9 cm,如果第三边的长为整数,那么第三边的长为( )
A.8 cm或10 cm B.8 cm或9 cm
C.8 cm D.10 cm
6.如图,点A,D,C,F在一条直线上,AB=DE,∠A=∠EDF,下列条件不能判定△ABC≌△DEF的是( )。
A.AD=CF B.∠BCA=∠F
C.∠B=∠E D.BC=EF
7.已知函数y=kx+b的图象如图所示,则函数y=-bx+k的图象大致是
(
第
8
题图
)8. 如图,OP是∠的平分线,点P到OA的距离为3,点
N是OB上的任意一点,则线段PN的取值范围为( )
B. C. D.
如图,将矩形纸片ABCD折叠,使点D与点B重合,点C 落在处,折痕为EF,若,,则△ 和的周长之和为( )
A. 3 B. 4 C. 6 D. 8
10.有下列四个命题:①相等的角是对顶角;②同位角相等; (
第
9
题图
) ③若一个角的两边与另一个角的两边互相平行,则这两个 角一定相等;④从直线外一点到这条直线的垂线段,叫做点到直线的距离,其中是真命题的个数有( )
A. 0个 B. 1个 C. 2个 D. 3个
二、填空题(本大题共4小题,每小题5分,满分20分)
11. 如图,把“QQ”笑脸放在直角坐标系中,已知左眼A的坐标是(-2,3),嘴唇C点的坐标为(-1,1),则此“QQ” 笑脸右眼B的坐标_______________ .
如图,在平面直角坐标系xOy中,△由△绕点P旋转得到,则点P的
坐标为_____________.
(
第
12
题图
)
已知函数是正比例函数,则 _________
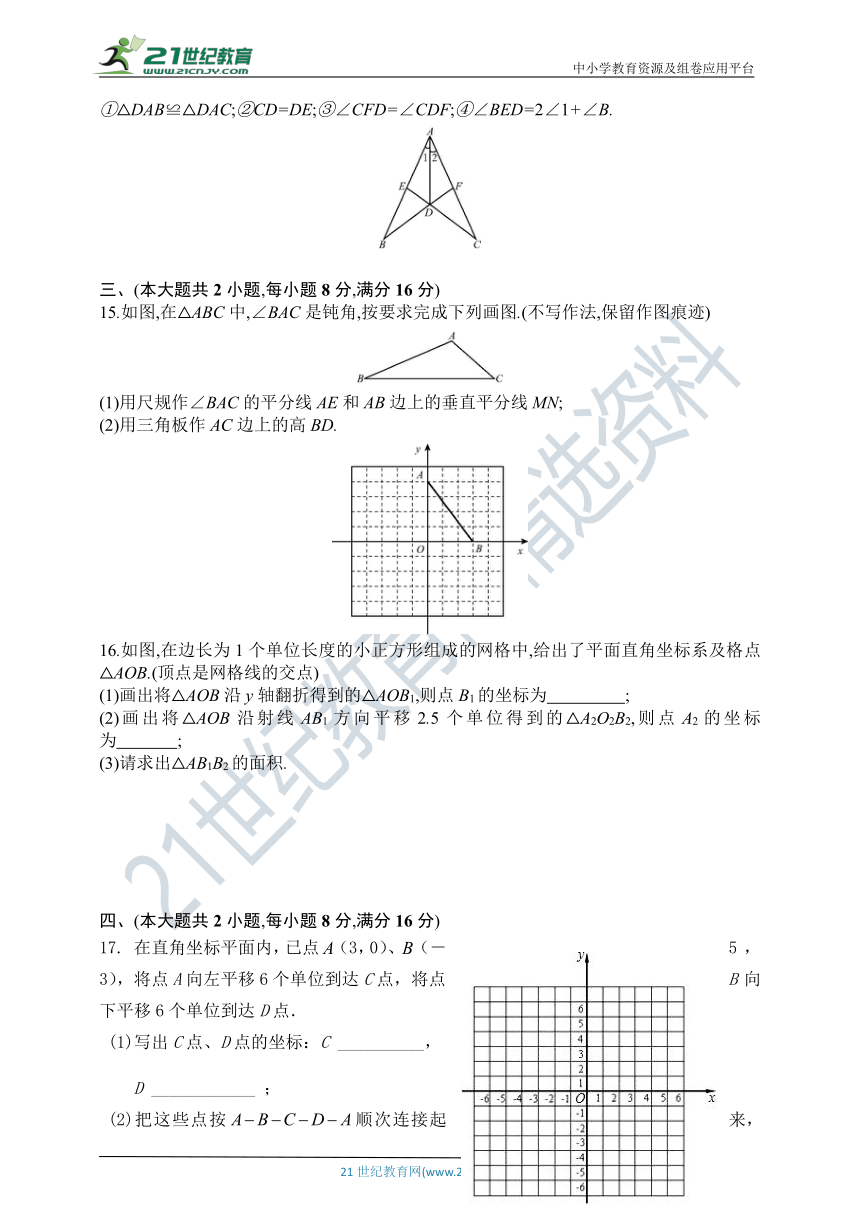
14.如图,∠1=∠2,∠C=∠B,下列结论中正确的是 .(写出所有正确结论的序号)
①△DAB≌△DAC;②CD=DE;③∠CFD=∠CDF;④∠BED=2∠1+∠B.
三、(本大题共2小题,每小题8分,满分16分)
15.如图,在△ABC中,∠BAC是钝角,按要求完成下列画图.(不写作法,保留作图痕迹)
(1)用尺规作∠BAC的平分线AE和AB边上的垂直平分线MN;
(2)用三角板作AC边上的高BD.
16.如图,在边长为1个单位长度的小正方形组成的网格中,给出了平面直角坐标系及格点△AOB.(顶点是网格线的交点)
(1)画出将△AOB沿y轴翻折得到的△AOB1,则点B1的坐标为 ;
(2)画出将△AOB沿射线AB1方向平移2.5个单位得到的△A2O2B2,则点A2的坐标为 ;
(3)请求出△AB1B2的面积.
四、(本大题共2小题,每小题8分,满分16分)
17. 在直角坐标平面内,已点(3,0)、(-5,3),将点A向左平移6个单位到达C点,将点B向下平移6个单位到达D点.
(1)写出C点、D点的坐标:C __________,
D ____________ ;
(2)把这些点按顺次连接起来,这个图形的面积是__________.
18. 已知点关于x轴的对称点在第一象限,求a的取值范围.
五、(本大题共2小题,每小题10分,满分20分)
19.小明平时喜欢玩“宾果消消乐”游戏.本学期在学校组织的几次数学反馈性测试中,小明的数学成绩如下表:
月份x 9 10 11 12 13(第二年元月) 14(第二年2月)
成绩y(分) 90 80 70 60 … …
(1)以月份为x轴,成绩为y轴,根据上表提供的数据在平面直角坐标系中描点;
(2)观察(1)中所描点的位置关系,猜想y与x之间的函数关系,并求出所猜想的函数表达式;
(3)若小明继续沉溺于“宾果消消乐”游戏,照这样的发展趋势,请你估计元月(此时x=13)份的考试中小明的数学成绩,并用一句话对小明提出一些建议。
20.如图,在Rt△ABC中,∠ACB=90°,∠A=22.5°,斜边AB的垂直平分线交AC于点D,点F在AC上,点E在BC的延长线上,CE=CF,连接BF,DE.则线段DE和BF在数量和位置上有什么关系 请说明理由.
六、(本题满分12分)
21.某学校开展“青少年科技创新比赛”活动,“喜洋洋”代表队设计了一个遥控车沿直线轨道AC做匀速直线运动的模型.甲、乙两车同时分别从A,B出发,沿轨道到达C处,在AC上,甲的速度是乙的速度的1.5倍,设t分后甲、乙两遥控车与B处的距离分别为d1,d2(单位:米),则d1,d2与t的函数关系如图,试根据图象解决下列问题.
(1)填空:乙的速度v2= 米/分;
(2)写出d1与t的函数表达式;
(3)若甲、乙两遥控车的距离超过10米时信号不会产生相互干扰,试探究什么时间两遥控车的信号不会产生相互干扰
七、(本题满分12分)
22.在平面直角坐标系xOy中,已知定点A(1,0)和B(0,1).
(1)如图1,若动点C在x轴上运动,则使△ABC为等腰三角形的点C有几个
(2)如图2,过点A,B向过原点的直线l作垂线,垂足分别为M,N,试判断线段AM,BN,MN之间的数量关系,并说明理由.
(本题满分14分)
23. 种植草莓大户张华现有22吨草莓等待出售,有两种销售渠道,一是运往省城直接批发给零售商,二是在本地市场零售,受客观因素影响,张华每天只能采用一种销售渠道,而且草莓必须在10天内售出(含10天)经过调查分析,这两种销售渠道每天销量及每吨所获纯利润见右表:(12分)
销售渠道 每日销量(吨) 每吨所获纯利润(元)
省城批发 4 1200
本地零售 1 2000
(1)若一部分草莓运往省城批发给零售商,其余在本地市场零售,请写出销售22吨草莓所获纯利润(元)与运往省城直接批发零售商的草莓量(吨)之间的函数关系式;
(2)怎样安排这22吨草莓的销售渠道,才使张华所获纯利润最大?并求出最大纯利润。
参考答案:
一、1. D 2. B 3. A 4.D 5.A 6.D 7.C 8. C 9.C 10.A
二、11. 12. 13. 2 14. ①④
三、15.解:如图所示.
16.解:(1) (-3,0)
(2) (-1.5,2).
(3)△AB1B2的面积=4.5×6-×3×4-×1.5×6-×4.5×2=12.
四、17. ;;18
18. 解:依题意得p点在第四象限,
,
解得:,即a的取值范围是.
五、19.解:(1)如图.
(2)猜想:y是x的一次函数.
设y=kx+b,把点(9,90),(10,80)代入得解得∴y=-10x+180.
经验证,点(11,70)和(12,60)均在直线y=-10x+180上,
∴y与x之间的函数表达式为y=-10x+180.
(3)∵当x=13时,y=50,
∴估计元月份的考试中小明的数学成绩是50分.
建议:不要再沉迷于游戏,要好好学习.
20.解:DE=BF,DE⊥BF.理由如下:
连接BD,延长BF交DE于点G.
∵点D在线段AB的垂直平分线上,
∴AD=BD,∴∠ABD=∠A=22.5°.
在Rt△ABC中,∵∠ACB=90°,∠A=22.5°,
∴∠ABC=67.5°,∴∠CBD=∠ABC-∠ABD=45°,
∴△BCD为等腰直角三角形,∴BC=DC.
在△ECD和△FCB中,
∴△ECD≌△FCB(SAS),
∴DE=BF,∠CED=∠CFB.
∵∠CFB+∠CBF=90°,∴∠CED+∠CBF=90°,
∴∠EGB=90°,即DE⊥BF.
六、21.(1)40 (2)v1=1.5v2=1.5×40=60(米/分),
60÷60=1(分钟),a=1,
∴d1=
(3)由已知可得AB=60米,BC=120米,v1=60米/分,v2=40米/分,并且在0≤t≤3时,乙车始终在甲车前面,
当0≤t<1时,甲车未达到B点,所以甲、乙两遥控车的距离为40t-60t+60=-20t+60>10,解得t<2.5.所以0≤t<1时,两车距离始终大于10米,信号不会产生相互干扰.
当1≤t≤3时,甲车经过B点向C点行驶,此时甲、乙两遥控车的距离为40t+60-60t>10,解得t<2.5,所以1≤t<2.5时,两车不会产生信号干扰.
∴当0≤t<2.5时,两遥控车的信号不会产生相互干扰.
七、22.
解:(1)如图,当以AB为腰时,有3个;当以AB为底时,有1个,
∴使△ABC为等腰三角形的点C有4个.
(2)AM+BN=MN.
理由:由已知可得OA=OB,∠AOM=90°-∠BON=∠OBN,
在△AOM和△OBN中,
∴△AOM≌△OBN(AAS),
∴AM=ON,OM=BN,
∴AM+BN=ON+OM=MN.
八、23. 解:由题意可得,,
即销售22吨草莓所获纯利润元与运往省城直接批发零售商的草莓量吨之间的函数关系式是;
草莓必须在10天内售出含10天,
,
解得,,
,
在函数中,y随x的增大而减小,
当时,y取得最大值,此时,
,
即用4天时间运往省城批发,6天在本地零售,可以使张华所获纯利润最大,最大利润为31200元.
当时,,解得
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
21世纪教育网(www.21cnjy.com)
2023年沪科版数学八年级上册期末测试题(一)
(时间:120分钟 分值:120分)
一、选择题(本大题共10小题,每小题4分,满分40分)
1. 点P在x轴的下方,且距离x轴3个单位长度,距离y轴4个单位长度,则点P的坐标 为( )
(4,-3) B. (3,-4)
C. (-3,-4)或(3,-4) D. (-4,-3)或(4,-3)
2. 若三条线段中,,为奇数,那么由a、b、c为边组成的三角形共有( )
A. 1个 B. 3个 C. 无数多个 D. 无法确定
3. 在同一直角坐标系中,若直线与直线平行,则( )
A., B., C., D.,
4.在以下节水、回收、节能、绿色食品四个标志中,是轴对称图形的是
5.已知非等腰三角形的两边长分别是2 cm和9 cm,如果第三边的长为整数,那么第三边的长为( )
A.8 cm或10 cm B.8 cm或9 cm
C.8 cm D.10 cm
6.如图,点A,D,C,F在一条直线上,AB=DE,∠A=∠EDF,下列条件不能判定△ABC≌△DEF的是( )。
A.AD=CF B.∠BCA=∠F
C.∠B=∠E D.BC=EF
7.已知函数y=kx+b的图象如图所示,则函数y=-bx+k的图象大致是
(
第
8
题图
)8. 如图,OP是∠的平分线,点P到OA的距离为3,点
N是OB上的任意一点,则线段PN的取值范围为( )
B. C. D.
如图,将矩形纸片ABCD折叠,使点D与点B重合,点C 落在处,折痕为EF,若,,则△ 和的周长之和为( )
A. 3 B. 4 C. 6 D. 8
10.有下列四个命题:①相等的角是对顶角;②同位角相等; (
第
9
题图
) ③若一个角的两边与另一个角的两边互相平行,则这两个 角一定相等;④从直线外一点到这条直线的垂线段,叫做点到直线的距离,其中是真命题的个数有( )
A. 0个 B. 1个 C. 2个 D. 3个
二、填空题(本大题共4小题,每小题5分,满分20分)
11. 如图,把“QQ”笑脸放在直角坐标系中,已知左眼A的坐标是(-2,3),嘴唇C点的坐标为(-1,1),则此“QQ” 笑脸右眼B的坐标_______________ .
如图,在平面直角坐标系xOy中,△由△绕点P旋转得到,则点P的
坐标为_____________.
(
第
12
题图
)
已知函数是正比例函数,则 _________
14.如图,∠1=∠2,∠C=∠B,下列结论中正确的是 .(写出所有正确结论的序号)
①△DAB≌△DAC;②CD=DE;③∠CFD=∠CDF;④∠BED=2∠1+∠B.
三、(本大题共2小题,每小题8分,满分16分)
15.如图,在△ABC中,∠BAC是钝角,按要求完成下列画图.(不写作法,保留作图痕迹)
(1)用尺规作∠BAC的平分线AE和AB边上的垂直平分线MN;
(2)用三角板作AC边上的高BD.
16.如图,在边长为1个单位长度的小正方形组成的网格中,给出了平面直角坐标系及格点△AOB.(顶点是网格线的交点)
(1)画出将△AOB沿y轴翻折得到的△AOB1,则点B1的坐标为 ;
(2)画出将△AOB沿射线AB1方向平移2.5个单位得到的△A2O2B2,则点A2的坐标为 ;
(3)请求出△AB1B2的面积.
四、(本大题共2小题,每小题8分,满分16分)
17. 在直角坐标平面内,已点(3,0)、(-5,3),将点A向左平移6个单位到达C点,将点B向下平移6个单位到达D点.
(1)写出C点、D点的坐标:C __________,
D ____________ ;
(2)把这些点按顺次连接起来,这个图形的面积是__________.
18. 已知点关于x轴的对称点在第一象限,求a的取值范围.
五、(本大题共2小题,每小题10分,满分20分)
19.小明平时喜欢玩“宾果消消乐”游戏.本学期在学校组织的几次数学反馈性测试中,小明的数学成绩如下表:
月份x 9 10 11 12 13(第二年元月) 14(第二年2月)
成绩y(分) 90 80 70 60 … …
(1)以月份为x轴,成绩为y轴,根据上表提供的数据在平面直角坐标系中描点;
(2)观察(1)中所描点的位置关系,猜想y与x之间的函数关系,并求出所猜想的函数表达式;
(3)若小明继续沉溺于“宾果消消乐”游戏,照这样的发展趋势,请你估计元月(此时x=13)份的考试中小明的数学成绩,并用一句话对小明提出一些建议。
20.如图,在Rt△ABC中,∠ACB=90°,∠A=22.5°,斜边AB的垂直平分线交AC于点D,点F在AC上,点E在BC的延长线上,CE=CF,连接BF,DE.则线段DE和BF在数量和位置上有什么关系 请说明理由.
六、(本题满分12分)
21.某学校开展“青少年科技创新比赛”活动,“喜洋洋”代表队设计了一个遥控车沿直线轨道AC做匀速直线运动的模型.甲、乙两车同时分别从A,B出发,沿轨道到达C处,在AC上,甲的速度是乙的速度的1.5倍,设t分后甲、乙两遥控车与B处的距离分别为d1,d2(单位:米),则d1,d2与t的函数关系如图,试根据图象解决下列问题.
(1)填空:乙的速度v2= 米/分;
(2)写出d1与t的函数表达式;
(3)若甲、乙两遥控车的距离超过10米时信号不会产生相互干扰,试探究什么时间两遥控车的信号不会产生相互干扰
七、(本题满分12分)
22.在平面直角坐标系xOy中,已知定点A(1,0)和B(0,1).
(1)如图1,若动点C在x轴上运动,则使△ABC为等腰三角形的点C有几个
(2)如图2,过点A,B向过原点的直线l作垂线,垂足分别为M,N,试判断线段AM,BN,MN之间的数量关系,并说明理由.
(本题满分14分)
23. 种植草莓大户张华现有22吨草莓等待出售,有两种销售渠道,一是运往省城直接批发给零售商,二是在本地市场零售,受客观因素影响,张华每天只能采用一种销售渠道,而且草莓必须在10天内售出(含10天)经过调查分析,这两种销售渠道每天销量及每吨所获纯利润见右表:(12分)
销售渠道 每日销量(吨) 每吨所获纯利润(元)
省城批发 4 1200
本地零售 1 2000
(1)若一部分草莓运往省城批发给零售商,其余在本地市场零售,请写出销售22吨草莓所获纯利润(元)与运往省城直接批发零售商的草莓量(吨)之间的函数关系式;
(2)怎样安排这22吨草莓的销售渠道,才使张华所获纯利润最大?并求出最大纯利润。
参考答案:
一、1. D 2. B 3. A 4.D 5.A 6.D 7.C 8. C 9.C 10.A
二、11. 12. 13. 2 14. ①④
三、15.解:如图所示.
16.解:(1) (-3,0)
(2) (-1.5,2).
(3)△AB1B2的面积=4.5×6-×3×4-×1.5×6-×4.5×2=12.
四、17. ;;18
18. 解:依题意得p点在第四象限,
,
解得:,即a的取值范围是.
五、19.解:(1)如图.
(2)猜想:y是x的一次函数.
设y=kx+b,把点(9,90),(10,80)代入得解得∴y=-10x+180.
经验证,点(11,70)和(12,60)均在直线y=-10x+180上,
∴y与x之间的函数表达式为y=-10x+180.
(3)∵当x=13时,y=50,
∴估计元月份的考试中小明的数学成绩是50分.
建议:不要再沉迷于游戏,要好好学习.
20.解:DE=BF,DE⊥BF.理由如下:
连接BD,延长BF交DE于点G.
∵点D在线段AB的垂直平分线上,
∴AD=BD,∴∠ABD=∠A=22.5°.
在Rt△ABC中,∵∠ACB=90°,∠A=22.5°,
∴∠ABC=67.5°,∴∠CBD=∠ABC-∠ABD=45°,
∴△BCD为等腰直角三角形,∴BC=DC.
在△ECD和△FCB中,
∴△ECD≌△FCB(SAS),
∴DE=BF,∠CED=∠CFB.
∵∠CFB+∠CBF=90°,∴∠CED+∠CBF=90°,
∴∠EGB=90°,即DE⊥BF.
六、21.(1)40 (2)v1=1.5v2=1.5×40=60(米/分),
60÷60=1(分钟),a=1,
∴d1=
(3)由已知可得AB=60米,BC=120米,v1=60米/分,v2=40米/分,并且在0≤t≤3时,乙车始终在甲车前面,
当0≤t<1时,甲车未达到B点,所以甲、乙两遥控车的距离为40t-60t+60=-20t+60>10,解得t<2.5.所以0≤t<1时,两车距离始终大于10米,信号不会产生相互干扰.
当1≤t≤3时,甲车经过B点向C点行驶,此时甲、乙两遥控车的距离为40t+60-60t>10,解得t<2.5,所以1≤t<2.5时,两车不会产生信号干扰.
∴当0≤t<2.5时,两遥控车的信号不会产生相互干扰.
七、22.
解:(1)如图,当以AB为腰时,有3个;当以AB为底时,有1个,
∴使△ABC为等腰三角形的点C有4个.
(2)AM+BN=MN.
理由:由已知可得OA=OB,∠AOM=90°-∠BON=∠OBN,
在△AOM和△OBN中,
∴△AOM≌△OBN(AAS),
∴AM=ON,OM=BN,
∴AM+BN=ON+OM=MN.
八、23. 解:由题意可得,,
即销售22吨草莓所获纯利润元与运往省城直接批发零售商的草莓量吨之间的函数关系式是;
草莓必须在10天内售出含10天,
,
解得,,
,
在函数中,y随x的增大而减小,
当时,y取得最大值,此时,
,
即用4天时间运往省城批发,6天在本地零售,可以使张华所获纯利润最大,最大利润为31200元.
当时,,解得
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
21世纪教育网(www.21cnjy.com)
同课章节目录
