2023年沪科版数学八年级上册期末测试题及答案(二)(含答案)
文档属性
| 名称 | 2023年沪科版数学八年级上册期末测试题及答案(二)(含答案) |  | |
| 格式 | docx | ||
| 文件大小 | 1.2MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 沪科版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-09-13 23:53:04 | ||
图片预览


文档简介
中小学教育资源及组卷应用平台
2023年沪科版数学八年级上册期末测试题(二)
(时间:120分钟 分值:120分)
一、选择题(本大题共10小题,共40分)
1.将点M(-5,y)向下平移6个单位长度后所得到的点与点M关于x轴对称,则y的值是( )。
A.-6 B.6
C.-3 D.3
2.下列命题与其逆命题都是真命题的是( )。
A.全等三角形对应角相等 B.对顶角相等
C.角平分线上的点到角的两边的距离相等 D.若a2>b2,则a>b
3.把一副三角板按如图叠放在一起,则∠α的度数是
A.165° B.160° C.155° D.150°
4. 点关于y轴对称的点的坐标是( )。
A. (1,2) B. (-1,2) C. (-1,-2) D. (-2,1)
5. 有一个角是的等腰三角形,其它两个角的度数是( )。
A. 36°,108° B. 36°,72°
C. 72°,72° D. 36°,108°或72°,°72°
6. 当,时,函数的图象大致是( )。
A. B. C. D.
7. 有以下四个命题:其中正确的个数为( )。
(1)两条对角线互相平分的四边形是平行四边形;
(2)两条对角线相等的四边形是矩形;
(3)两条对角线互相垂直的平行四边形是菱形;
(4)有一组邻边相等且有一个角是直角的四边形是正方形;
A. 1 B. 2 C. 3 D. 4
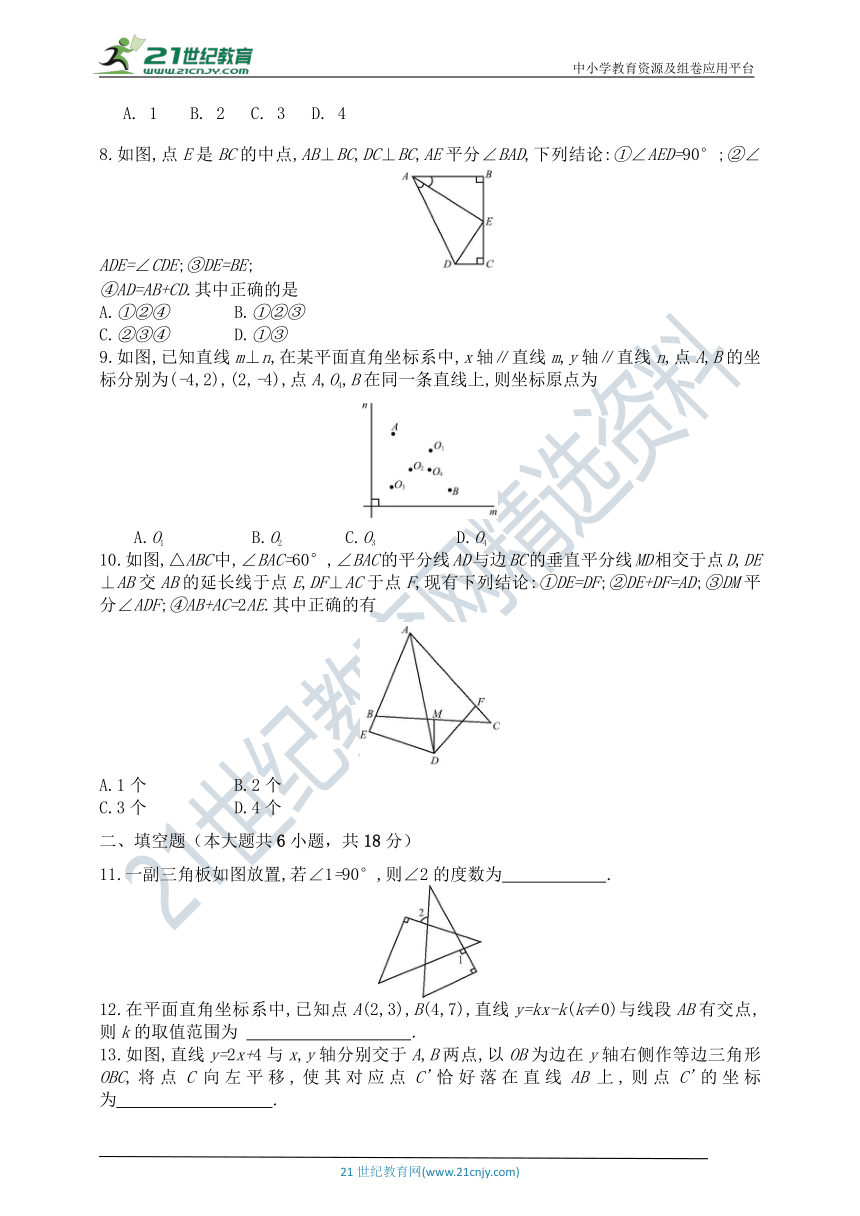
8.如图,点E是BC的中点,AB⊥BC,DC⊥BC,AE平分∠BAD,下列结论:①∠AED=90°;②∠ADE=∠CDE;③DE=BE;
④AD=AB+CD.其中正确的是
A.①②④ B.①②③
C.②③④ D.①③
9.如图,已知直线m⊥n,在某平面直角坐标系中,x轴∥直线m,y轴∥直线n,点A,B的坐标分别为(-4,2),(2,-4),点A,O4,B在同一条直线上,则坐标原点为
A.O1 B.O2 C.O3 D.O4
10.如图,△ABC中,∠BAC=60°,∠BAC的平分线AD与边BC的垂直平分线MD相交于点D,DE⊥AB交AB的延长线于点E,DF⊥AC于点F,现有下列结论:①DE=DF;②DE+DF=AD;③DM平分∠ADF;④AB+AC=2AE.其中正确的有
A.1个 B.2个
C.3个 D.4个
二、填空题(本大题共6小题,共18分)
11.一副三角板如图放置,若∠1=90°,则∠2的度数为 .
12.在平面直角坐标系中,已知点A(2,3),B(4,7),直线y=kx-k(k≠0)与线段AB有交点,则k的取值范围为 .
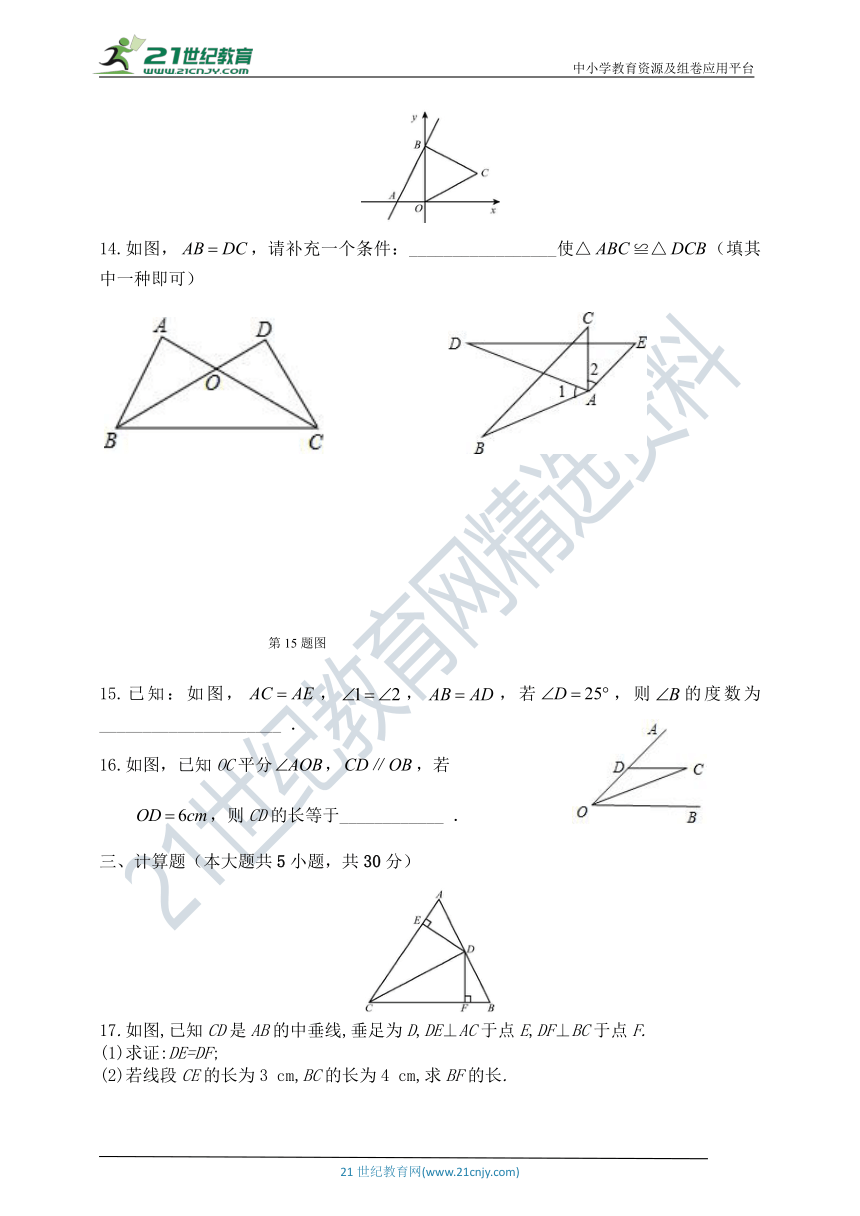
13.如图,直线y=2x+4与x,y轴分别交于A,B两点,以OB为边在y轴右侧作等边三角形OBC,将点C向左平移,使其对应点C'恰好落在直线AB上,则点C'的坐标为 .
14.如图,,请补充一个条件:_________________使△≌△(填其中一种即可)
(
第
15
题图
) (
第
14
题图
)
15.已知:如图,,,,若,则的度数为_____________________ .
16.如图,已知OC平分,,若
,则CD的长等于____________ .
三、计算题(本大题共5小题,共30分)
17.如图,已知CD是AB的中垂线,垂足为D,DE⊥AC于点E,DF⊥BC于点F.
(1)求证:DE=DF;
(2)若线段CE的长为3 cm,BC的长为4 cm,求BF的长.
18.已知:如图1,在Rt△ABC和Rt△A'B'C'中,AB=A'B',AC=A'C',C=∠C'=90°.
求证:Rt△ABC和Rt△A'B'C'全等.
(1)请你用“如果…,那么…”的形式叙述上述命题;
(2)将△ABC和△A'B'C'拼在一起,请你画出两种拼接图形;例如图2:(即使点A与点A'重合,点C与点C'重合.)
(3)请你选择你拼成的其中一种图形,证明该命题.
如图是屋架设计图的一部分,其中,点D是斜梁AB的中点,BC、DE垂直于
横梁,,则立柱,要多长?
20. 我国西南五省市的部分地区发生严重旱灾,为鼓励节约用水,某市自来水公司采取分段收费标准,右图反映的是每月收取水费元与用水量吨之间的函数关系.
(1) 小明家五月份用水8吨,应交水费______ 元;
(2) 按上述分段收费标准,小明家三、四月份分别交水费26元和18元,问四月份比三月份节约用水多少吨?
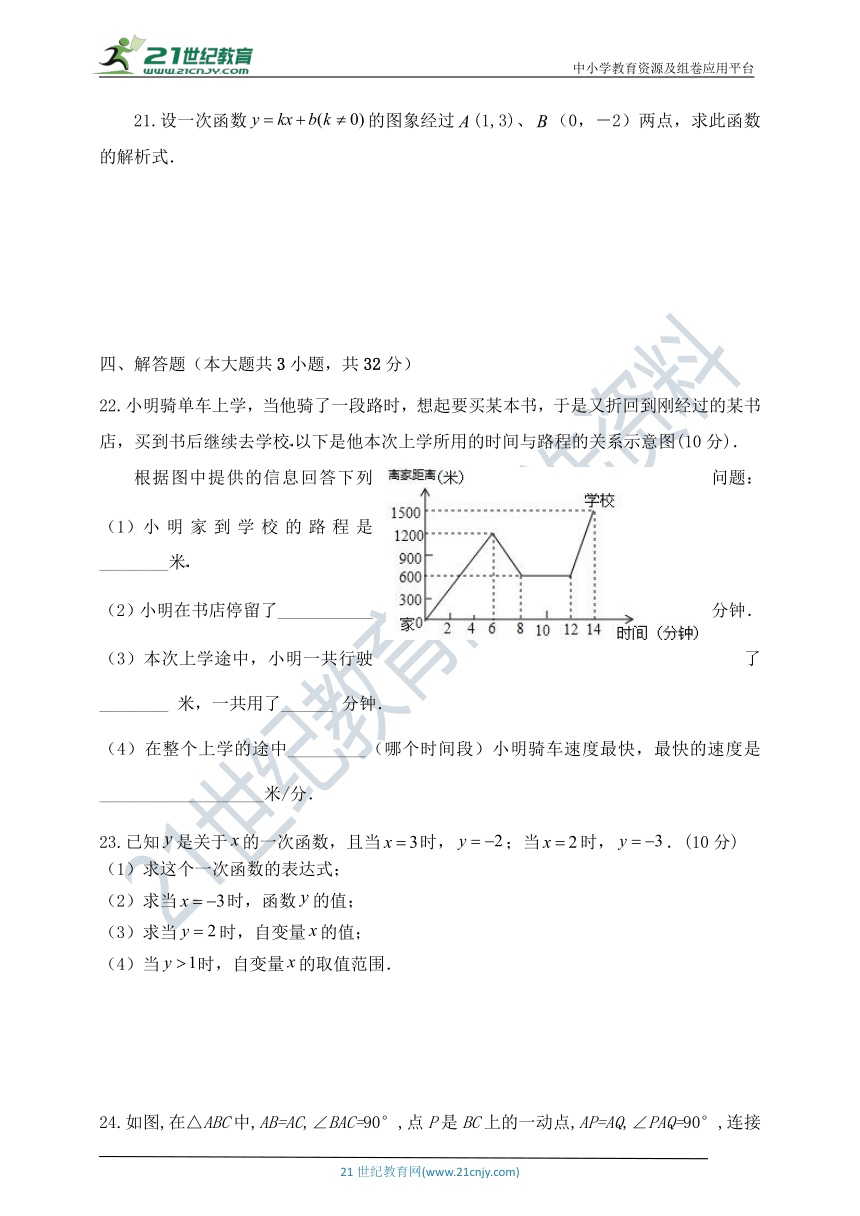
21.设一次函数的图象经过(1,3)、(0,-2)两点,求此函数的解析式.
解答题(本大题共3小题,共32分)
22.小明骑单车上学,当他骑了一段路时,想起要买某本书,于是又折回到刚经过的某书店,买到书后继续去学校以下是他本次上学所用的时间与路程的关系示意图(10分).
根据图中提供的信息回答下列问题:
小明家到学校的路程是________米
(2)小明在书店停留了___________分钟.
(3)本次上学途中,小明一共行驶了________ 米,一共用了______ 分钟.
(4)在整个上学的途中_________(哪个时间段)小明骑车速度最快,最快的速度是___________________米/分.
23.已知是关于的一次函数,且当时,;当时,.(10分)
(1)求这个一次函数的表达式;
(2)求当时,函数的值;
(3)求当时,自变量的值;
(4)当时,自变量的取值范围.
24.如图,在△ABC中,AB=AC,∠BAC=90°,点P是BC上的一动点,AP=AQ,∠PAQ=90°,连接CQ.
(1)求证:CQ⊥BC.
(2)△ACQ能否是直角三角形 若能,请直接写出此时点P的位置;若不能,请说明理由.
(3)当点P在BC上什么位置时,△ACQ是等腰三角形 请说明理由.
参考答案
一、1.D 2.C 3.A 4. C 5. D 6. D 7. B 8.A 9.A 10.C
二、11. 75° 12. ≤k≤3 13. (-1,2)
14.
15.
16. 6cm
三、17.解:(1)∵CD是AB的中垂线,
∴AC=BC,
∴∠ACD=∠BCD,
∵DE⊥AC,DF⊥BC,
∴DE=DF.
(2)∵DE⊥AC,DF⊥BC,∴∠AED=∠BFD=90°,
在Rt△ADE和Rt△BDF中,
∴Rt△ADE≌Rt△BDF(HL),
∴AE=BF,
∵CE=3 cm,BC=4 cm,
∴BF=AE=AC-CE=BC-CE=1 cm.
18.解:(1)如果一个直角三角形的斜边和一条直角边与另一个直角三角形的斜边和一条直角边分别相等,那么这两个直角三角形全等.
(2)如图:
图①使点A与点A'重合,点B与点B'重合.
图②使点A与点B'重合,点B与点A'重合.
(3)在图①中,∵点A和点A'重合,点B和点B'重合,连接CC'.
∵AC=A'C',∴∠ACC'=∠AC'C,
∵∠ACB=∠A'C'B'=90°,∴∠ACB-∠ACC'=∠A'C'B'-∠AC'C,
即∠BCC'=∠BC'C,
∴BC=B'C'.
在Rt△ABC和Rt△A'B'C'中,
∴△ABC≌△A'B'C'(SSS).
19. 解:,
,
、DE垂直于横梁AC,
,又D是AB的中点,
,
答:立柱BC要要2m.
20. 解:根据图象可知,10吨以内每吨水应缴元
所以元.
解法一:
由图可得用水10吨内每吨2元,10吨以上每吨元
三月份交水费26元元所以用水:吨
四月份交水费18元元,所以用水:吨
四月份比三月份节约用水:吨
解法二:
由图可得10吨内每吨2元,当时,知
当时,可设y与x的关系为:
由图可知,当时,时,可解得
与x之间的函数关系式为:,
当时,知,有,解得,
四月份比三月份节约用水:吨.
直接根据图象先求得10吨以内每吨水应缴元,再求小明家的水费;
根据图象求得10吨以上每吨3元,3月份交水费26元元,故水费按照超过10吨,每吨3元计算;四月份交水费18元元,故水费按照每吨2元计算,分别计算用水量做差即可求出节约的水量.
主要考查了一次函数的实际应用和读图的基本能力解题的关键是能根据函数图象得到函数类型,并根据函数图象上点的实际意义求解.
21. 解:把、代入得,解得,
所以此函数解析式为.
四、22.1500;4;2700;14;12分钟至14分钟;450
23.. 解:设一次函数的表达式为由题意,得
,
解得.
所以,该一次函数解析式为:;
当时,;
当时,,解得.
当时,,解得
24. 解:(1)∵∠BAP+∠CAP=∠BAC=90°,∠CAQ+∠CAP=∠PAQ=90°,
∴∠BAP=∠CAQ,
在△ABP和△ACQ中,
∴△ABP≌△ACQ(SAS),
∴∠ACQ=∠B,
∵AB=AC,∠BAC=90°,
∴∠B=∠ACB=45°,
∴∠BCQ=∠ACB+∠ACQ=45°+45°=90°,
∴CQ⊥BC.
(2)当点P为BC的中点或与点C重合时,△ACQ是直角三角形.
(3)①当BP=AB时,△ABP是等腰三角形;
②当AB=AP时,点P与点C重合;
③当AP=BP时,点P为BC的中点.
∵△ABP≌△ACQ,
∴当点P为BC的中点或与点C重合或BP=AB时,△ACQ是等腰三角形。
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
21世纪教育网(www.21cnjy.com)
2023年沪科版数学八年级上册期末测试题(二)
(时间:120分钟 分值:120分)
一、选择题(本大题共10小题,共40分)
1.将点M(-5,y)向下平移6个单位长度后所得到的点与点M关于x轴对称,则y的值是( )。
A.-6 B.6
C.-3 D.3
2.下列命题与其逆命题都是真命题的是( )。
A.全等三角形对应角相等 B.对顶角相等
C.角平分线上的点到角的两边的距离相等 D.若a2>b2,则a>b
3.把一副三角板按如图叠放在一起,则∠α的度数是
A.165° B.160° C.155° D.150°
4. 点关于y轴对称的点的坐标是( )。
A. (1,2) B. (-1,2) C. (-1,-2) D. (-2,1)
5. 有一个角是的等腰三角形,其它两个角的度数是( )。
A. 36°,108° B. 36°,72°
C. 72°,72° D. 36°,108°或72°,°72°
6. 当,时,函数的图象大致是( )。
A. B. C. D.
7. 有以下四个命题:其中正确的个数为( )。
(1)两条对角线互相平分的四边形是平行四边形;
(2)两条对角线相等的四边形是矩形;
(3)两条对角线互相垂直的平行四边形是菱形;
(4)有一组邻边相等且有一个角是直角的四边形是正方形;
A. 1 B. 2 C. 3 D. 4
8.如图,点E是BC的中点,AB⊥BC,DC⊥BC,AE平分∠BAD,下列结论:①∠AED=90°;②∠ADE=∠CDE;③DE=BE;
④AD=AB+CD.其中正确的是
A.①②④ B.①②③
C.②③④ D.①③
9.如图,已知直线m⊥n,在某平面直角坐标系中,x轴∥直线m,y轴∥直线n,点A,B的坐标分别为(-4,2),(2,-4),点A,O4,B在同一条直线上,则坐标原点为
A.O1 B.O2 C.O3 D.O4
10.如图,△ABC中,∠BAC=60°,∠BAC的平分线AD与边BC的垂直平分线MD相交于点D,DE⊥AB交AB的延长线于点E,DF⊥AC于点F,现有下列结论:①DE=DF;②DE+DF=AD;③DM平分∠ADF;④AB+AC=2AE.其中正确的有
A.1个 B.2个
C.3个 D.4个
二、填空题(本大题共6小题,共18分)
11.一副三角板如图放置,若∠1=90°,则∠2的度数为 .
12.在平面直角坐标系中,已知点A(2,3),B(4,7),直线y=kx-k(k≠0)与线段AB有交点,则k的取值范围为 .
13.如图,直线y=2x+4与x,y轴分别交于A,B两点,以OB为边在y轴右侧作等边三角形OBC,将点C向左平移,使其对应点C'恰好落在直线AB上,则点C'的坐标为 .
14.如图,,请补充一个条件:_________________使△≌△(填其中一种即可)
(
第
15
题图
) (
第
14
题图
)
15.已知:如图,,,,若,则的度数为_____________________ .
16.如图,已知OC平分,,若
,则CD的长等于____________ .
三、计算题(本大题共5小题,共30分)
17.如图,已知CD是AB的中垂线,垂足为D,DE⊥AC于点E,DF⊥BC于点F.
(1)求证:DE=DF;
(2)若线段CE的长为3 cm,BC的长为4 cm,求BF的长.
18.已知:如图1,在Rt△ABC和Rt△A'B'C'中,AB=A'B',AC=A'C',C=∠C'=90°.
求证:Rt△ABC和Rt△A'B'C'全等.
(1)请你用“如果…,那么…”的形式叙述上述命题;
(2)将△ABC和△A'B'C'拼在一起,请你画出两种拼接图形;例如图2:(即使点A与点A'重合,点C与点C'重合.)
(3)请你选择你拼成的其中一种图形,证明该命题.
如图是屋架设计图的一部分,其中,点D是斜梁AB的中点,BC、DE垂直于
横梁,,则立柱,要多长?
20. 我国西南五省市的部分地区发生严重旱灾,为鼓励节约用水,某市自来水公司采取分段收费标准,右图反映的是每月收取水费元与用水量吨之间的函数关系.
(1) 小明家五月份用水8吨,应交水费______ 元;
(2) 按上述分段收费标准,小明家三、四月份分别交水费26元和18元,问四月份比三月份节约用水多少吨?
21.设一次函数的图象经过(1,3)、(0,-2)两点,求此函数的解析式.
解答题(本大题共3小题,共32分)
22.小明骑单车上学,当他骑了一段路时,想起要买某本书,于是又折回到刚经过的某书店,买到书后继续去学校以下是他本次上学所用的时间与路程的关系示意图(10分).
根据图中提供的信息回答下列问题:
小明家到学校的路程是________米
(2)小明在书店停留了___________分钟.
(3)本次上学途中,小明一共行驶了________ 米,一共用了______ 分钟.
(4)在整个上学的途中_________(哪个时间段)小明骑车速度最快,最快的速度是___________________米/分.
23.已知是关于的一次函数,且当时,;当时,.(10分)
(1)求这个一次函数的表达式;
(2)求当时,函数的值;
(3)求当时,自变量的值;
(4)当时,自变量的取值范围.
24.如图,在△ABC中,AB=AC,∠BAC=90°,点P是BC上的一动点,AP=AQ,∠PAQ=90°,连接CQ.
(1)求证:CQ⊥BC.
(2)△ACQ能否是直角三角形 若能,请直接写出此时点P的位置;若不能,请说明理由.
(3)当点P在BC上什么位置时,△ACQ是等腰三角形 请说明理由.
参考答案
一、1.D 2.C 3.A 4. C 5. D 6. D 7. B 8.A 9.A 10.C
二、11. 75° 12. ≤k≤3 13. (-1,2)
14.
15.
16. 6cm
三、17.解:(1)∵CD是AB的中垂线,
∴AC=BC,
∴∠ACD=∠BCD,
∵DE⊥AC,DF⊥BC,
∴DE=DF.
(2)∵DE⊥AC,DF⊥BC,∴∠AED=∠BFD=90°,
在Rt△ADE和Rt△BDF中,
∴Rt△ADE≌Rt△BDF(HL),
∴AE=BF,
∵CE=3 cm,BC=4 cm,
∴BF=AE=AC-CE=BC-CE=1 cm.
18.解:(1)如果一个直角三角形的斜边和一条直角边与另一个直角三角形的斜边和一条直角边分别相等,那么这两个直角三角形全等.
(2)如图:
图①使点A与点A'重合,点B与点B'重合.
图②使点A与点B'重合,点B与点A'重合.
(3)在图①中,∵点A和点A'重合,点B和点B'重合,连接CC'.
∵AC=A'C',∴∠ACC'=∠AC'C,
∵∠ACB=∠A'C'B'=90°,∴∠ACB-∠ACC'=∠A'C'B'-∠AC'C,
即∠BCC'=∠BC'C,
∴BC=B'C'.
在Rt△ABC和Rt△A'B'C'中,
∴△ABC≌△A'B'C'(SSS).
19. 解:,
,
、DE垂直于横梁AC,
,又D是AB的中点,
,
答:立柱BC要要2m.
20. 解:根据图象可知,10吨以内每吨水应缴元
所以元.
解法一:
由图可得用水10吨内每吨2元,10吨以上每吨元
三月份交水费26元元所以用水:吨
四月份交水费18元元,所以用水:吨
四月份比三月份节约用水:吨
解法二:
由图可得10吨内每吨2元,当时,知
当时,可设y与x的关系为:
由图可知,当时,时,可解得
与x之间的函数关系式为:,
当时,知,有,解得,
四月份比三月份节约用水:吨.
直接根据图象先求得10吨以内每吨水应缴元,再求小明家的水费;
根据图象求得10吨以上每吨3元,3月份交水费26元元,故水费按照超过10吨,每吨3元计算;四月份交水费18元元,故水费按照每吨2元计算,分别计算用水量做差即可求出节约的水量.
主要考查了一次函数的实际应用和读图的基本能力解题的关键是能根据函数图象得到函数类型,并根据函数图象上点的实际意义求解.
21. 解:把、代入得,解得,
所以此函数解析式为.
四、22.1500;4;2700;14;12分钟至14分钟;450
23.. 解:设一次函数的表达式为由题意,得
,
解得.
所以,该一次函数解析式为:;
当时,;
当时,,解得.
当时,,解得
24. 解:(1)∵∠BAP+∠CAP=∠BAC=90°,∠CAQ+∠CAP=∠PAQ=90°,
∴∠BAP=∠CAQ,
在△ABP和△ACQ中,
∴△ABP≌△ACQ(SAS),
∴∠ACQ=∠B,
∵AB=AC,∠BAC=90°,
∴∠B=∠ACB=45°,
∴∠BCQ=∠ACB+∠ACQ=45°+45°=90°,
∴CQ⊥BC.
(2)当点P为BC的中点或与点C重合时,△ACQ是直角三角形.
(3)①当BP=AB时,△ABP是等腰三角形;
②当AB=AP时,点P与点C重合;
③当AP=BP时,点P为BC的中点.
∵△ABP≌△ACQ,
∴当点P为BC的中点或与点C重合或BP=AB时,△ACQ是等腰三角形。
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
21世纪教育网(www.21cnjy.com)
同课章节目录
