【高效备课】人教版七(上) 2.2 整式的加减 第3课时 整式的加减 课件
文档属性
| 名称 | 【高效备课】人教版七(上) 2.2 整式的加减 第3课时 整式的加减 课件 |  | |
| 格式 | pptx | ||
| 文件大小 | 193.7KB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-09-12 16:36:58 | ||
图片预览








文档简介
(共21张PPT)
2.2 整式的加减
第3课时 整式的加减
R·七年级上册
新课导入
导入课题
前面我们学习了合并同类项,去括号等知识,它们是进行整式加减运算的基础,这节课我们来学习整式的加减运算.
学习目标
(1)能熟练进行整式加减运算.
(2)能运用整式加减运算解决简单的实际问题.
推进新课
知识点1
整式的加减
例6 计算
(1)( 2x – 3y ) + ( 5x + 4y )
= 2x – 3y + 5x + 4y
= 7x + y
(2)( 8a – 7b ) – ( 4a – 5b )
= 8a – 7b – 4a +5b
= 4a – 2b
例7 笔记本的单价是x元,圆珠笔的单价是y元. 小红买3本笔记本,2支圆珠笔;小明买4本笔记本,3支圆珠笔.买这些笔记本和圆珠笔,小红和小明一共花费多少钱?
解法1:小红买笔记本和圆珠笔共花费(3x+2y)元,小明买笔记本和圆珠笔共花费(4x+3y)元.
小红和小明一共花费(单位:元):
(3x+2y) + (4x+3y) = 7x+5y
解法2:小红和小明买笔记本共花费(3x+4x)元,买圆珠笔共花费(2y+3y)元.
小红和小明一共花费(单位:元):
(3x+4x) + (2y+3y) = 7x+5y
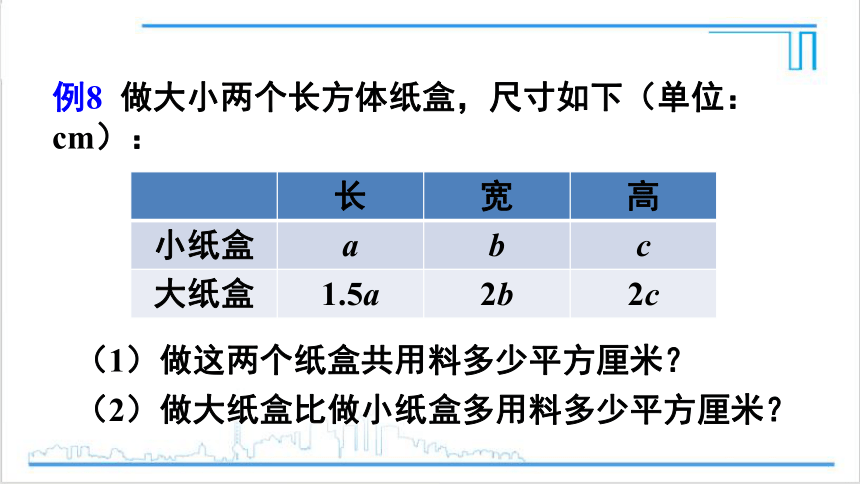
例8 做大小两个长方体纸盒,尺寸如下(单位:
cm):
长 宽 高
小纸盒 a b c
大纸盒 1.5a 2b 2c
(1)做这两个纸盒共用料多少平方厘米?
(2)做大纸盒比做小纸盒多用料多少平方厘米?
解:小纸盒的表面积是(2ab+2bc+2ca)cm2
大纸盒的表面积是(6ab+8bc+6ca)cm2
(1)做这两个纸盒共用料(单位:cm2):
(2ab+2bc+2ca)+ (6ab+8bc+6ca)
= 8ab+10bc+8ca
(2)做大纸盒比做小纸盒多用料(单位:cm2)
(6ab+8bc+6ca)- (2ab+2bc+2ca)
=4ab+6bc+4ca
通过上面的学习,我们可以得到整式加减的运算法则:
一般地,几个整式相加减,如果有括号就先去括号,然后再合并同类项.
例9 求 的值,其中
x = – 2,y = .
解:
当x= – 2,y = 时,原式
先将式子化简,再代入数值进行计算比较简便.
练习1 计算
巩固练习
(1)3xy – 4xy –(– 2xy)
= 3xy – 4xy + 2xy
= xy
【课本P69 练习 第1题】
练习2 计算
(1)( – x + 2x2 + 5)+(4x2 – 3 – 6x)
= – x + 2x2 + 5 + 4x2 – 3 – 6x
= 6x2 –7x + 2
(2)( 3a2 – ab + 7)–(– 4a2 + 2ab + 7)
=3a2 – ab + 7+ 4a2 – 2ab – 7
=7a2 – 3ab
【课本P69 练习 第2题】
练习3 计算先化简下式,再求值.
5(3a2b – ab2)–(ab2+3a2b),
解:原式= 15a2b – 5ab2 – ab2 – 3a2b
= 12a2b – 6ab2
其中 , .
当 , 时
原式=
【课本P69 练习 第3题】
随堂演练
基础巩固
1. 计算:
(1)(5a + 4c + 7b)+(5c – 3b – 6a)
解:原式= 5a + 4c + 7b + 5c – 3b – 6a
= – a + 4b + 9c
(2)(8xy – x2 + y2)–(x2 – y2 + 8xy)
解:原式= 8xy – x2 + y2 – x2 + y2 – 8xy
= – 2x2 + 2y2
(3)(2x2 – + 3x)– 4(x – x2 + )
解:原式= 2x2 – + 3x – 4x + 4x2 – 2
= 6x2 – x –
(4)3x2 –[7x –(4x – 3)– 2x2]
解:原式= 3x2 –(7x – 4x + 3 – 2x2)
= 3x2 – 7x + 4x – 3 + 2x2
= 5x2 – 3x – 3
综合应用
2. 窗户的形状如图所示(图中长度单位:cm),其上部是半圆形,下部是边长相同的四个小正方形. 已知下部小正方形的边长是a cm,计算:
(1)窗户的面积;
(2)窗户外框的总长.
解:(1)窗户的面积为
+4a2= (cm2)
(2)窗户的外框总长是:
πa+2a×3=πa+6a
=(π+6)a(cm)
3. 观察下列图形并填表(单位:cm).
梯形个数 1 2 3 4 5 6 … n
图形周长 5a 8a 11a …
14a
17a
20a
(3n+2)a
拓展延伸
4. (1)一个两位数的个位上的数是a,十位上的数是b,列式表示这个两位数.
解:(1)10b + a;
(2)列式表示上面的两位数与10的乘积.
(2)10(10b + a);
(3)列式表示(1)中的两位数与它的10倍的和,这个和是11的倍数吗?为什么?
(3)10b + a + 10(10b + a)= 11(10b + a),这个和是11的倍数,因为它含有11这个因数.
课堂小结
通过上面的学习,我们可以得到整式加减的运算法则:
一般地,几个整式相加减,如果有括号就先去括号,然后再合并同类项.
课后作业
1.从课后习题中选取;
2.完成练习册本课时的习题。
2.2 整式的加减
第3课时 整式的加减
R·七年级上册
新课导入
导入课题
前面我们学习了合并同类项,去括号等知识,它们是进行整式加减运算的基础,这节课我们来学习整式的加减运算.
学习目标
(1)能熟练进行整式加减运算.
(2)能运用整式加减运算解决简单的实际问题.
推进新课
知识点1
整式的加减
例6 计算
(1)( 2x – 3y ) + ( 5x + 4y )
= 2x – 3y + 5x + 4y
= 7x + y
(2)( 8a – 7b ) – ( 4a – 5b )
= 8a – 7b – 4a +5b
= 4a – 2b
例7 笔记本的单价是x元,圆珠笔的单价是y元. 小红买3本笔记本,2支圆珠笔;小明买4本笔记本,3支圆珠笔.买这些笔记本和圆珠笔,小红和小明一共花费多少钱?
解法1:小红买笔记本和圆珠笔共花费(3x+2y)元,小明买笔记本和圆珠笔共花费(4x+3y)元.
小红和小明一共花费(单位:元):
(3x+2y) + (4x+3y) = 7x+5y
解法2:小红和小明买笔记本共花费(3x+4x)元,买圆珠笔共花费(2y+3y)元.
小红和小明一共花费(单位:元):
(3x+4x) + (2y+3y) = 7x+5y
例8 做大小两个长方体纸盒,尺寸如下(单位:
cm):
长 宽 高
小纸盒 a b c
大纸盒 1.5a 2b 2c
(1)做这两个纸盒共用料多少平方厘米?
(2)做大纸盒比做小纸盒多用料多少平方厘米?
解:小纸盒的表面积是(2ab+2bc+2ca)cm2
大纸盒的表面积是(6ab+8bc+6ca)cm2
(1)做这两个纸盒共用料(单位:cm2):
(2ab+2bc+2ca)+ (6ab+8bc+6ca)
= 8ab+10bc+8ca
(2)做大纸盒比做小纸盒多用料(单位:cm2)
(6ab+8bc+6ca)- (2ab+2bc+2ca)
=4ab+6bc+4ca
通过上面的学习,我们可以得到整式加减的运算法则:
一般地,几个整式相加减,如果有括号就先去括号,然后再合并同类项.
例9 求 的值,其中
x = – 2,y = .
解:
当x= – 2,y = 时,原式
先将式子化简,再代入数值进行计算比较简便.
练习1 计算
巩固练习
(1)3xy – 4xy –(– 2xy)
= 3xy – 4xy + 2xy
= xy
【课本P69 练习 第1题】
练习2 计算
(1)( – x + 2x2 + 5)+(4x2 – 3 – 6x)
= – x + 2x2 + 5 + 4x2 – 3 – 6x
= 6x2 –7x + 2
(2)( 3a2 – ab + 7)–(– 4a2 + 2ab + 7)
=3a2 – ab + 7+ 4a2 – 2ab – 7
=7a2 – 3ab
【课本P69 练习 第2题】
练习3 计算先化简下式,再求值.
5(3a2b – ab2)–(ab2+3a2b),
解:原式= 15a2b – 5ab2 – ab2 – 3a2b
= 12a2b – 6ab2
其中 , .
当 , 时
原式=
【课本P69 练习 第3题】
随堂演练
基础巩固
1. 计算:
(1)(5a + 4c + 7b)+(5c – 3b – 6a)
解:原式= 5a + 4c + 7b + 5c – 3b – 6a
= – a + 4b + 9c
(2)(8xy – x2 + y2)–(x2 – y2 + 8xy)
解:原式= 8xy – x2 + y2 – x2 + y2 – 8xy
= – 2x2 + 2y2
(3)(2x2 – + 3x)– 4(x – x2 + )
解:原式= 2x2 – + 3x – 4x + 4x2 – 2
= 6x2 – x –
(4)3x2 –[7x –(4x – 3)– 2x2]
解:原式= 3x2 –(7x – 4x + 3 – 2x2)
= 3x2 – 7x + 4x – 3 + 2x2
= 5x2 – 3x – 3
综合应用
2. 窗户的形状如图所示(图中长度单位:cm),其上部是半圆形,下部是边长相同的四个小正方形. 已知下部小正方形的边长是a cm,计算:
(1)窗户的面积;
(2)窗户外框的总长.
解:(1)窗户的面积为
+4a2= (cm2)
(2)窗户的外框总长是:
πa+2a×3=πa+6a
=(π+6)a(cm)
3. 观察下列图形并填表(单位:cm).
梯形个数 1 2 3 4 5 6 … n
图形周长 5a 8a 11a …
14a
17a
20a
(3n+2)a
拓展延伸
4. (1)一个两位数的个位上的数是a,十位上的数是b,列式表示这个两位数.
解:(1)10b + a;
(2)列式表示上面的两位数与10的乘积.
(2)10(10b + a);
(3)列式表示(1)中的两位数与它的10倍的和,这个和是11的倍数吗?为什么?
(3)10b + a + 10(10b + a)= 11(10b + a),这个和是11的倍数,因为它含有11这个因数.
课堂小结
通过上面的学习,我们可以得到整式加减的运算法则:
一般地,几个整式相加减,如果有括号就先去括号,然后再合并同类项.
课后作业
1.从课后习题中选取;
2.完成练习册本课时的习题。
