【高效备课】人教版七(上) 3.2 解一元一次方程(一)——合并同类项与移项 第1课时 合并同类项 课件
文档属性
| 名称 | 【高效备课】人教版七(上) 3.2 解一元一次方程(一)——合并同类项与移项 第1课时 合并同类项 课件 |

|
|
| 格式 | pptx | ||
| 文件大小 | 378.3KB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-09-12 16:36:58 | ||
图片预览










文档简介
(共31张PPT)
第1课时 合并同类项
R·七年级上册
3.2 解一元一次方程(一)
——合并同类项与移项
新课导入
导入课题
同学们还记得什么是同类项吗?如何合并同类项吗?
上节课,我们学习了利用等式的性质解一些简单的方程,这节课我们来学习如何利用合并同类项和等式的性质解一些形式较复杂的方程.
学习目标
(1)会利用合并同类项的方法解一元一次方程,体会等式变形中的化归思想.
(2)能够从实际问题中列出一元一次方程,进一步体会方程模型思想的作用及应用价值.
推进新课
知识点1
合并同类项
数学小资料
约公元820年,中亚细亚数学家阿尔-花拉子米写了一本代数书,重点论述怎样解方程.这本书的拉丁文译本取名为《对消与还原》. “对消”与“还原”是什么意思呢?
问题1
某校三年共购买计算机140台,去年购买数量是前年的2倍,今年购买数量又是去年的2倍.前年这个学校购买了多少台计算机?
方法一:
设前年这个学校购买了计算机x台,则去年购买计算机 2x台,今年购买计算机4x台.
前年购买量+去年购买量+今年购买量=140台
根据题意,列得方程
x+2x+4x=140.
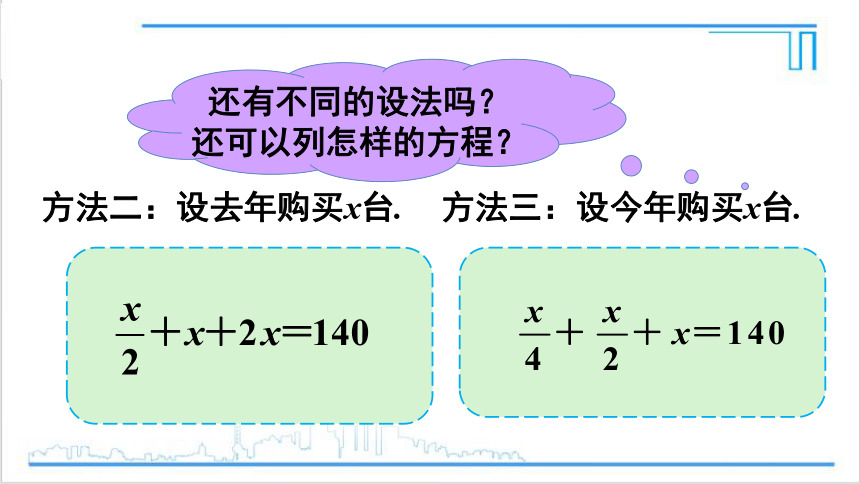
还有不同的设法吗?
还可以列怎样的方程?
方法二:设去年购买x台.
方法三:设今年购买x台.
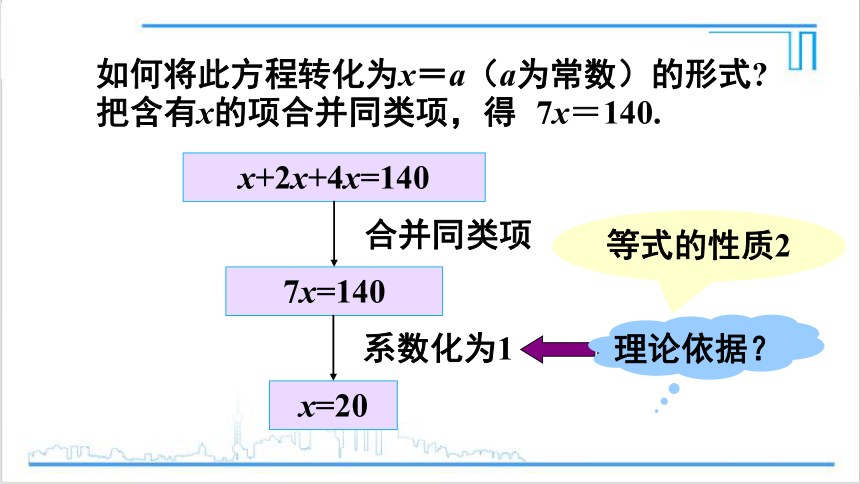
如何将此方程转化为x=a(a为常数)的形式
把含有x的项合并同类项,得
7x=140.
x+2x+4x=140
合并同类项
系数化为1
等式的性质2
理论依据?
7x=140
x=20
回顾本题列方程的过程,可以发现:“总量=各部分量的和”是一个基本的相等关系.
思考
在解方程过程中,合并同类项起了什么作用?
合并同类项的目的就是化简方程,
它是一种恒等变形,可以使方程变得简单,并逐步使方程向x=a的形式转化.
知识点2
解方程
例1 解下列方程:
解:合并同类项,得
系数化为1,得 x = 4
(1)
(2)7x-2.5x+3x-1.5x=-15×4-6×3
解:合并同类项,得
6x = -78
系数化为1,得 x = -13
例2 有一列数,按一定规律排列成1,-3,9,-27,81,-243,···.其中某三个相邻数的和是-1 701,这三个数各是多少?
分析:从符号和绝对值两方面观察,可发现这列数的排列规律:后面的数是它前面的数与-3的乘积.如果三个相邻数中的第1个记为x,则后两个数分别是-3x,9x.
解:设所求三个数分别是x,-3x,9x.
由三个数的和是-1701,得 x - 3x + 9x = -1701.
合并同类项,得 7x = -1701.
系数化为1,得 x = -243.
所以-3x = 729 , 9x= -2187.
答:这三个数是-243,729,-2187.
若设所求的三个数中,中间的一个数为x,则它前面的一个数为 ,它后面的一个数为-3x,于是,依题意可列方程
+ x - 3x = -1701.
并求出所列方程的解.
x = 729.
若设所求的三个数中第三个数为x,则第一个数为 ,第二个数为 . 依题意可列方程
并求出所列方程的解.
x = -2187
巩固练习
练习 解下列方程:
解:合并同类项,得
系数化为1,得
(1)5x - 2x = 9
3x = 9
x = 3
【课本P88 练习 第1题】
解:合并同类项,得
系数化为1,得
【课本P88 练习 第1题】
(3)-3x + 0.5x = 10
解:合并同类项,得
-2.5x = 10
系数化为1,得
x = -4
【课本P88 练习 第1题】
(4)7x - 4.5x = 2.5×3 - 5
解:合并同类项,得
系数化为1,得
2.5x = 2.5
x = 1
【课本P88 练习 第1题】
【课本P88 练习 第2题】
某工厂的产值连续增长,去年是前年的1.5倍,今年是去年的2倍,这三年的总产值为550万元.前年的产值是多少
随堂演练
基础巩固
1.解下列方程:
(1)2x + 3x + 4x = 18
解:合并同类项,得
9x = 18
系数化为1,得
x = 2
(2)13x - 15x + x = -3
解:合并同类项,得
-x = -3
系数化为1,得
x = 3
(3)2.5y + 10y - 6y = 15 - 21.5
解:合并同类项,得
6.5y = - 6.5
系数化为1,得
y = -1
(4)
解:合并同类项,得
系数化为1,得
2. 有一列数:1,-2,4,-8,16,…,若其中三个相邻数的和是312,求这三个数.
解:设这三个数中的第一个数为x,则第二个数为-2x,第三个数为4x.
则由题意,得 x - 2x + 4x = 312.
解得 x = 104.
-2x = -208,4x = 416.
答:这三个数是104,-208,416.
综合应用
3. 随着农业技术的现代化,节水型灌溉得到了逐步推广,喷灌和滴灌是比漫灌节水的灌溉方式,灌溉三块同样大的实验田,第一块用漫灌方式,第二块用喷灌方式,第三块用滴灌方式,后两种方式用水量分别是漫灌的25%和15%.
(1)设第一块实验田用水x t,则另两块实验田的用水量如何表示?
(2)如果三块实验田共用水420 t,每块实验田各用水多少吨?
解:(1)设第一块实验田用水x t,则第二块实验田用水25%x t,第三块实验田用水15%x t.
(2)由(1)及已知,得
x + 25%x + 15%x = 420.
合并同类项,得 1.4x = 420.
系数化为1,得 x = 300.
所以25%x=75,15%x=45.
即第一块实验田用水300 t,则第二块实验田用水75 t,第三块实验田用水45 t.
拓展延伸
5. 有一列数:6,12,18,24,…,从中取出三个相邻的数.
(1)若这三个相邻的数的和为324,求这三个数.
解:设这三个数中的第一个数为6x,则第二个数为6(x+1),第三个数为6(x+2).则由题意,得
6x +6( x+1) + 6( x + 2) = 324.
解得 x = 17.
所以6x =102,6( x+1) = 108,6(x + 2) = 114.
即这三个数为102,108,114.
5. 有一列数:6,12,18,24,…,从中取出三个相邻的数.
(2)试判断这三个相邻的数的和能否等于84?若能,求出这三个数;若不能,请说明理由.
解:由题意可得第n个数为6n,则第(n-1)个数为6(n-1),第(n+1)个数为6(n+1).则
6(n-1)+6n+6(n+1)=84.
解得n=
因为n为正整数,所以这个解不符题意.
即这三个相邻的数的和不能等于84.
课堂小结
x+2x+4x=140
合并同类项
系数化为1
等式的性质2
理论依据?
7x=140
x=20
课后作业
1.从课后习题中选取;
2.完成练习册本课时的习题.
第1课时 合并同类项
R·七年级上册
3.2 解一元一次方程(一)
——合并同类项与移项
新课导入
导入课题
同学们还记得什么是同类项吗?如何合并同类项吗?
上节课,我们学习了利用等式的性质解一些简单的方程,这节课我们来学习如何利用合并同类项和等式的性质解一些形式较复杂的方程.
学习目标
(1)会利用合并同类项的方法解一元一次方程,体会等式变形中的化归思想.
(2)能够从实际问题中列出一元一次方程,进一步体会方程模型思想的作用及应用价值.
推进新课
知识点1
合并同类项
数学小资料
约公元820年,中亚细亚数学家阿尔-花拉子米写了一本代数书,重点论述怎样解方程.这本书的拉丁文译本取名为《对消与还原》. “对消”与“还原”是什么意思呢?
问题1
某校三年共购买计算机140台,去年购买数量是前年的2倍,今年购买数量又是去年的2倍.前年这个学校购买了多少台计算机?
方法一:
设前年这个学校购买了计算机x台,则去年购买计算机 2x台,今年购买计算机4x台.
前年购买量+去年购买量+今年购买量=140台
根据题意,列得方程
x+2x+4x=140.
还有不同的设法吗?
还可以列怎样的方程?
方法二:设去年购买x台.
方法三:设今年购买x台.
如何将此方程转化为x=a(a为常数)的形式
把含有x的项合并同类项,得
7x=140.
x+2x+4x=140
合并同类项
系数化为1
等式的性质2
理论依据?
7x=140
x=20
回顾本题列方程的过程,可以发现:“总量=各部分量的和”是一个基本的相等关系.
思考
在解方程过程中,合并同类项起了什么作用?
合并同类项的目的就是化简方程,
它是一种恒等变形,可以使方程变得简单,并逐步使方程向x=a的形式转化.
知识点2
解方程
例1 解下列方程:
解:合并同类项,得
系数化为1,得 x = 4
(1)
(2)7x-2.5x+3x-1.5x=-15×4-6×3
解:合并同类项,得
6x = -78
系数化为1,得 x = -13
例2 有一列数,按一定规律排列成1,-3,9,-27,81,-243,···.其中某三个相邻数的和是-1 701,这三个数各是多少?
分析:从符号和绝对值两方面观察,可发现这列数的排列规律:后面的数是它前面的数与-3的乘积.如果三个相邻数中的第1个记为x,则后两个数分别是-3x,9x.
解:设所求三个数分别是x,-3x,9x.
由三个数的和是-1701,得 x - 3x + 9x = -1701.
合并同类项,得 7x = -1701.
系数化为1,得 x = -243.
所以-3x = 729 , 9x= -2187.
答:这三个数是-243,729,-2187.
若设所求的三个数中,中间的一个数为x,则它前面的一个数为 ,它后面的一个数为-3x,于是,依题意可列方程
+ x - 3x = -1701.
并求出所列方程的解.
x = 729.
若设所求的三个数中第三个数为x,则第一个数为 ,第二个数为 . 依题意可列方程
并求出所列方程的解.
x = -2187
巩固练习
练习 解下列方程:
解:合并同类项,得
系数化为1,得
(1)5x - 2x = 9
3x = 9
x = 3
【课本P88 练习 第1题】
解:合并同类项,得
系数化为1,得
【课本P88 练习 第1题】
(3)-3x + 0.5x = 10
解:合并同类项,得
-2.5x = 10
系数化为1,得
x = -4
【课本P88 练习 第1题】
(4)7x - 4.5x = 2.5×3 - 5
解:合并同类项,得
系数化为1,得
2.5x = 2.5
x = 1
【课本P88 练习 第1题】
【课本P88 练习 第2题】
某工厂的产值连续增长,去年是前年的1.5倍,今年是去年的2倍,这三年的总产值为550万元.前年的产值是多少
随堂演练
基础巩固
1.解下列方程:
(1)2x + 3x + 4x = 18
解:合并同类项,得
9x = 18
系数化为1,得
x = 2
(2)13x - 15x + x = -3
解:合并同类项,得
-x = -3
系数化为1,得
x = 3
(3)2.5y + 10y - 6y = 15 - 21.5
解:合并同类项,得
6.5y = - 6.5
系数化为1,得
y = -1
(4)
解:合并同类项,得
系数化为1,得
2. 有一列数:1,-2,4,-8,16,…,若其中三个相邻数的和是312,求这三个数.
解:设这三个数中的第一个数为x,则第二个数为-2x,第三个数为4x.
则由题意,得 x - 2x + 4x = 312.
解得 x = 104.
-2x = -208,4x = 416.
答:这三个数是104,-208,416.
综合应用
3. 随着农业技术的现代化,节水型灌溉得到了逐步推广,喷灌和滴灌是比漫灌节水的灌溉方式,灌溉三块同样大的实验田,第一块用漫灌方式,第二块用喷灌方式,第三块用滴灌方式,后两种方式用水量分别是漫灌的25%和15%.
(1)设第一块实验田用水x t,则另两块实验田的用水量如何表示?
(2)如果三块实验田共用水420 t,每块实验田各用水多少吨?
解:(1)设第一块实验田用水x t,则第二块实验田用水25%x t,第三块实验田用水15%x t.
(2)由(1)及已知,得
x + 25%x + 15%x = 420.
合并同类项,得 1.4x = 420.
系数化为1,得 x = 300.
所以25%x=75,15%x=45.
即第一块实验田用水300 t,则第二块实验田用水75 t,第三块实验田用水45 t.
拓展延伸
5. 有一列数:6,12,18,24,…,从中取出三个相邻的数.
(1)若这三个相邻的数的和为324,求这三个数.
解:设这三个数中的第一个数为6x,则第二个数为6(x+1),第三个数为6(x+2).则由题意,得
6x +6( x+1) + 6( x + 2) = 324.
解得 x = 17.
所以6x =102,6( x+1) = 108,6(x + 2) = 114.
即这三个数为102,108,114.
5. 有一列数:6,12,18,24,…,从中取出三个相邻的数.
(2)试判断这三个相邻的数的和能否等于84?若能,求出这三个数;若不能,请说明理由.
解:由题意可得第n个数为6n,则第(n-1)个数为6(n-1),第(n+1)个数为6(n+1).则
6(n-1)+6n+6(n+1)=84.
解得n=
因为n为正整数,所以这个解不符题意.
即这三个相邻的数的和不能等于84.
课堂小结
x+2x+4x=140
合并同类项
系数化为1
等式的性质2
理论依据?
7x=140
x=20
课后作业
1.从课后习题中选取;
2.完成练习册本课时的习题.
