【高效备课】人教版七(上) 3.2 解一元一次方程(一)——合并同类项与移项 第2课时 移项 课件
文档属性
| 名称 | 【高效备课】人教版七(上) 3.2 解一元一次方程(一)——合并同类项与移项 第2课时 移项 课件 |

|
|
| 格式 | pptx | ||
| 文件大小 | 269.1KB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-09-12 00:00:00 | ||
图片预览








文档简介
(共23张PPT)
第2课时 移项
R·七年级上册
新课导入
导入课题
前面,我们学习了利用合并同类项解一元一次方程,所见到的方程基本上都是含未知数的项在等号的一边(左边),常数项在等号的另一边(右边),如果等号两边都有含未知数的项和常数项,那么这样的方程该怎样求解呢?这节课我们继续学习解一元一次方程的方法——移项.
学习目标
(1)理解移项法则,会解形如ax+b=cx+d的方程,体会等式变形中的化归思想.
(2)能够从实际问题中列出一元一次方程,进一步体会方程模型思想的作用及应用价值.
推进新课
知识点1
移项
问题2
把一些图书分给某班学生阅读,如果每人分3本,则剩余20本;如果每人分4本,则还缺25本.这个班有多少学生?
每人分3本,共分出3x本,加上剩余的20本,这批书共(3x+20)本.
每人分4本,需要4x本,减去缺的25本,这批书共(4x-25)本.
分析
设这个班有x名学生.
这批书的总数有几种表示方法?它们之间有什么关系?
表示这批书的总数的两个代数式相等.
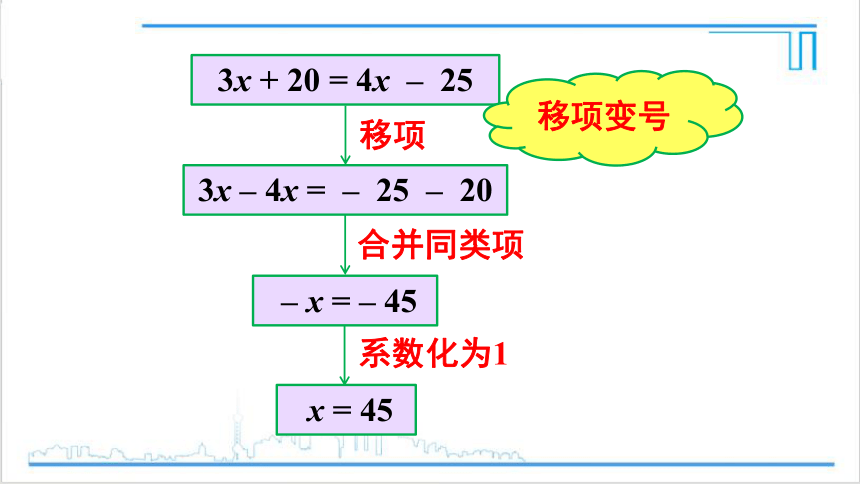
3x + 20 = 4x – 25
方程3x + 20 = 4x – 25的两边都有含x的项(3x与4x)和不含字母的常数项(20与– 25),怎样才能使它向x=a(常数)的形式转化呢?
思考
为了使方程的右边没有含x的项,等号两边减4x;为了使左边没有常数项,等号两边减20. 利用等式的性质1,得
3x – 4x = – 25 – 20.
上面方程的变形,相当于把原方程左边的20变为 – 20移到右边,把右边的4x变为 – 4x移到左边.
像上面那样把等式一边的某项变号后移到另一边,叫做移项.
3x + 20 = 4x – 25
3x – 4x = – 25 – 20
– x = – 45
x = 45
移项
合并同类项
系数化为1
移项变号
回顾本题列方程的过程,可以发现:“表示同一个量的两个不同的式子相等”是一个基本的相等关系.
思考
上面解方程中“移项”起了什么作用?
通过移项,含未知数的项与常数项分别位于方程左右两边,使方程更接近于x=a的形式.
知识点2
解方程
例3 解下列方程
(1)3x + 7 = 32 – 2x
解:移项,得
3x + 2x = 32 – 7
合并同类项,得
5x = 25
系数化为1,得
x = 5
解:移项,得
合并同类项,得
系数化为1,得
例4 某制药厂制造一批药品,如用旧工艺,则废水排量要比环保限制的最大量还多200 t;如用新工艺,则废水排量比环保限制的最大量少100 t. 新、旧工艺的废水排量之比为2∶5,两种工艺的废水排量各是多少?
分析:因为新、旧工艺的废水排量之比为2∶5,所以可设它们分别为2x t和5x t,再根据它们与环保限制的最大量之间的关系列方程.
解:设新、旧工艺的废水排量分别为2x t和5x t.根据废水排量与环保限制最大量之间的关系,得 5x-200=2x+100.
移项,得
5x-2x=100+200.
系数化为1,得 x=100.
合并同类项,得 3x=300.
所以 2x=200, 5x=500.
答:新、旧工艺产生的废水排量分别为200 t和500 t.
等号两边代表哪个数量?
练习1 解下列方程:
(1)6x – 7 = 4x – 5;
解:移项,得
合并同类项,得
系数化为1,得
6x – 4x = – 5 + 7
2x = 2.
x = 1.
巩固练习
【课本P90 练习 第1题】
解:移项,得
合并同类项,得
系数化为1,得
【课本P90 练习 第1题】
练习2 王芳和李丽同时采摘樱桃,王芳平均每小时采摘8 kg,李丽平均每小时采摘7 kg.采摘结束后王芳从她采摘的樱桃中取出0.25 kg给了李丽,这时两人的樱桃一样多,她们采摘用了多少时间?
解:设她们采摘用了x小时,则
8x – 0.25 = 7x + 0.25.
解得 x = 0.5.
答:她们采摘用了0.5小时.
【课本P90 练习 第1题】
随堂演练
基础巩固
1. 对于方程– 3x – 7=12x+6,下列移项正确的是( )
A
A. – 3x – 12x=6+7
B. – 3x+12x= – 7+6
C. – 3x – 12x=7-6
D.12x – 3x=6+7
2. 对方程 7x = 6 + 4x 进行移项,得___________,合并同类项,得_________,系数化为1,得________.
7x – 4x = 6
3x = 6
x = 2
综合应用
3. 小新出生时父亲28岁,现在父亲的年龄比小新年龄的3倍小2岁. 求小新现在的年龄.
解:设小新现在的年龄为x岁.
根据题意,得 3x – 2 = x + 28.
移项,得 2x = 30.
系数化为1,得 x = 15.
答:小新现在的年龄是15岁.
拓展延伸
4. 在一张普通的月历中,相邻三行里同一列的三个日期数之和能否为30?如果能,这三个数分别是多少?
解:设相邻三行里同一列的三个日期数分别为
x-7,x,x+7.
根据题意,得(x – 7)+x+(x+7)=30.
解得 x = 10.所以x – 7=3, x+7=17.
所以相邻三行里同一列的三个日期数之和能为30. 这三个数是3,10,17.
课堂小结
3x + 20 = 4x – 25
3x – 4x = – 25 – 20
– x = – 45
x = 45
移项
合并同类项
系数化为1
移项变号
课后作业
1.从课后习题中选取;
2.完成练习册本课时的习题.
第2课时 移项
R·七年级上册
新课导入
导入课题
前面,我们学习了利用合并同类项解一元一次方程,所见到的方程基本上都是含未知数的项在等号的一边(左边),常数项在等号的另一边(右边),如果等号两边都有含未知数的项和常数项,那么这样的方程该怎样求解呢?这节课我们继续学习解一元一次方程的方法——移项.
学习目标
(1)理解移项法则,会解形如ax+b=cx+d的方程,体会等式变形中的化归思想.
(2)能够从实际问题中列出一元一次方程,进一步体会方程模型思想的作用及应用价值.
推进新课
知识点1
移项
问题2
把一些图书分给某班学生阅读,如果每人分3本,则剩余20本;如果每人分4本,则还缺25本.这个班有多少学生?
每人分3本,共分出3x本,加上剩余的20本,这批书共(3x+20)本.
每人分4本,需要4x本,减去缺的25本,这批书共(4x-25)本.
分析
设这个班有x名学生.
这批书的总数有几种表示方法?它们之间有什么关系?
表示这批书的总数的两个代数式相等.
3x + 20 = 4x – 25
方程3x + 20 = 4x – 25的两边都有含x的项(3x与4x)和不含字母的常数项(20与– 25),怎样才能使它向x=a(常数)的形式转化呢?
思考
为了使方程的右边没有含x的项,等号两边减4x;为了使左边没有常数项,等号两边减20. 利用等式的性质1,得
3x – 4x = – 25 – 20.
上面方程的变形,相当于把原方程左边的20变为 – 20移到右边,把右边的4x变为 – 4x移到左边.
像上面那样把等式一边的某项变号后移到另一边,叫做移项.
3x + 20 = 4x – 25
3x – 4x = – 25 – 20
– x = – 45
x = 45
移项
合并同类项
系数化为1
移项变号
回顾本题列方程的过程,可以发现:“表示同一个量的两个不同的式子相等”是一个基本的相等关系.
思考
上面解方程中“移项”起了什么作用?
通过移项,含未知数的项与常数项分别位于方程左右两边,使方程更接近于x=a的形式.
知识点2
解方程
例3 解下列方程
(1)3x + 7 = 32 – 2x
解:移项,得
3x + 2x = 32 – 7
合并同类项,得
5x = 25
系数化为1,得
x = 5
解:移项,得
合并同类项,得
系数化为1,得
例4 某制药厂制造一批药品,如用旧工艺,则废水排量要比环保限制的最大量还多200 t;如用新工艺,则废水排量比环保限制的最大量少100 t. 新、旧工艺的废水排量之比为2∶5,两种工艺的废水排量各是多少?
分析:因为新、旧工艺的废水排量之比为2∶5,所以可设它们分别为2x t和5x t,再根据它们与环保限制的最大量之间的关系列方程.
解:设新、旧工艺的废水排量分别为2x t和5x t.根据废水排量与环保限制最大量之间的关系,得 5x-200=2x+100.
移项,得
5x-2x=100+200.
系数化为1,得 x=100.
合并同类项,得 3x=300.
所以 2x=200, 5x=500.
答:新、旧工艺产生的废水排量分别为200 t和500 t.
等号两边代表哪个数量?
练习1 解下列方程:
(1)6x – 7 = 4x – 5;
解:移项,得
合并同类项,得
系数化为1,得
6x – 4x = – 5 + 7
2x = 2.
x = 1.
巩固练习
【课本P90 练习 第1题】
解:移项,得
合并同类项,得
系数化为1,得
【课本P90 练习 第1题】
练习2 王芳和李丽同时采摘樱桃,王芳平均每小时采摘8 kg,李丽平均每小时采摘7 kg.采摘结束后王芳从她采摘的樱桃中取出0.25 kg给了李丽,这时两人的樱桃一样多,她们采摘用了多少时间?
解:设她们采摘用了x小时,则
8x – 0.25 = 7x + 0.25.
解得 x = 0.5.
答:她们采摘用了0.5小时.
【课本P90 练习 第1题】
随堂演练
基础巩固
1. 对于方程– 3x – 7=12x+6,下列移项正确的是( )
A
A. – 3x – 12x=6+7
B. – 3x+12x= – 7+6
C. – 3x – 12x=7-6
D.12x – 3x=6+7
2. 对方程 7x = 6 + 4x 进行移项,得___________,合并同类项,得_________,系数化为1,得________.
7x – 4x = 6
3x = 6
x = 2
综合应用
3. 小新出生时父亲28岁,现在父亲的年龄比小新年龄的3倍小2岁. 求小新现在的年龄.
解:设小新现在的年龄为x岁.
根据题意,得 3x – 2 = x + 28.
移项,得 2x = 30.
系数化为1,得 x = 15.
答:小新现在的年龄是15岁.
拓展延伸
4. 在一张普通的月历中,相邻三行里同一列的三个日期数之和能否为30?如果能,这三个数分别是多少?
解:设相邻三行里同一列的三个日期数分别为
x-7,x,x+7.
根据题意,得(x – 7)+x+(x+7)=30.
解得 x = 10.所以x – 7=3, x+7=17.
所以相邻三行里同一列的三个日期数之和能为30. 这三个数是3,10,17.
课堂小结
3x + 20 = 4x – 25
3x – 4x = – 25 – 20
– x = – 45
x = 45
移项
合并同类项
系数化为1
移项变号
课后作业
1.从课后习题中选取;
2.完成练习册本课时的习题.
