【高效备课】人教版七(上) 3.3 解一元一次方程(二)——去括号与去分母 第1课时 去括号 课件
文档属性
| 名称 | 【高效备课】人教版七(上) 3.3 解一元一次方程(二)——去括号与去分母 第1课时 去括号 课件 |

|
|
| 格式 | pptx | ||
| 文件大小 | 299.7KB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-09-12 00:00:00 | ||
图片预览





文档简介
(共25张PPT)
第1课时 去括号
R·七年级上册
3.3 解一元一次方程(二)
——去括号与去分母
新课导入
导入课题
前面我们已经学习了运用移项、合并同类项的方法解一元一次方程.对于像2(x–3)+3(x–1)=5这样的方程,又该怎么办呢?今天我们来学习含有括号的一元一次方程的解法.
学习目标
(1)会用去括号的方法解一元一次方程,进一步体会等式变形中的化归思想.
(2)进一步熟悉如何设未知数列方程解应用题,体会方程思想在解决实际问题的作用.
推进新课
知识点1
去括号
问题1
某工厂加强节能措施,去年下半年与上半年相比,月平均用电量减少2 000 kW·h(千瓦·时),全年用电15 万 kW·h.这个工厂去年上半年每月平均用电是多少?
月平均用电量×n(月数)=n个月用电量
温馨提示:
1 kW·h的电量是指1 kW的电器1 h的用电量.
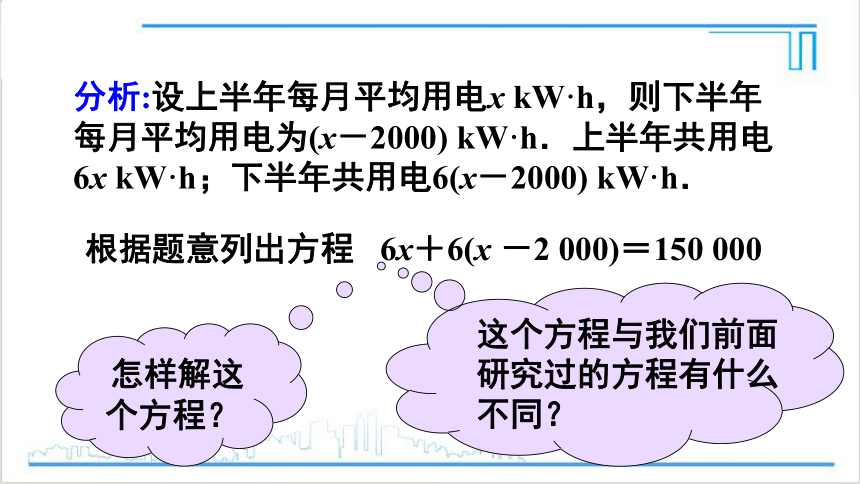
分析:设上半年每月平均用电x kW·h,则下半年每月平均用电为(x-2000) kW·h.上半年共用电6x kW·h;下半年共用电6(x-2000) kW·h.
6x+6(x -2 000)=150 000
根据题意列出方程
怎样解这个方程?
这个方程与我们前面
研究过的方程有什么
不同?
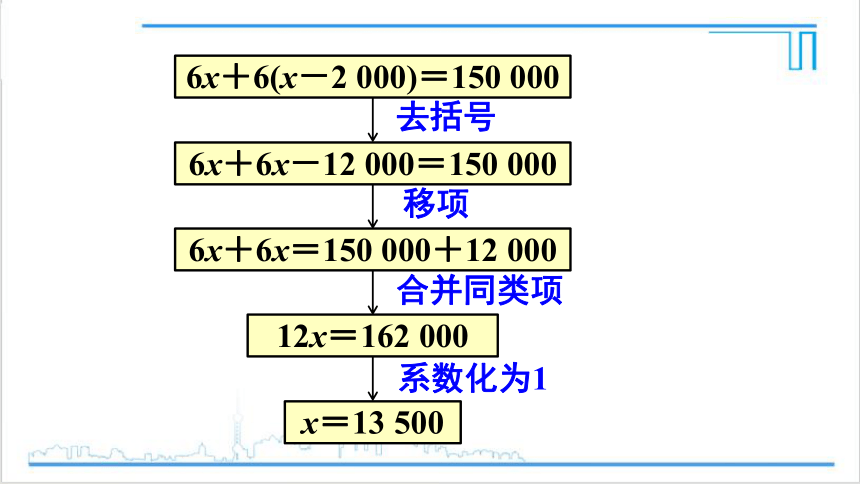
6x+6(x-2 000)=150 000
6x+6x-12 000=150 000
6x+6x=150 000+12 000
12x=162 000
x=13 500
去括号
合并同类项
移项
系数化为1
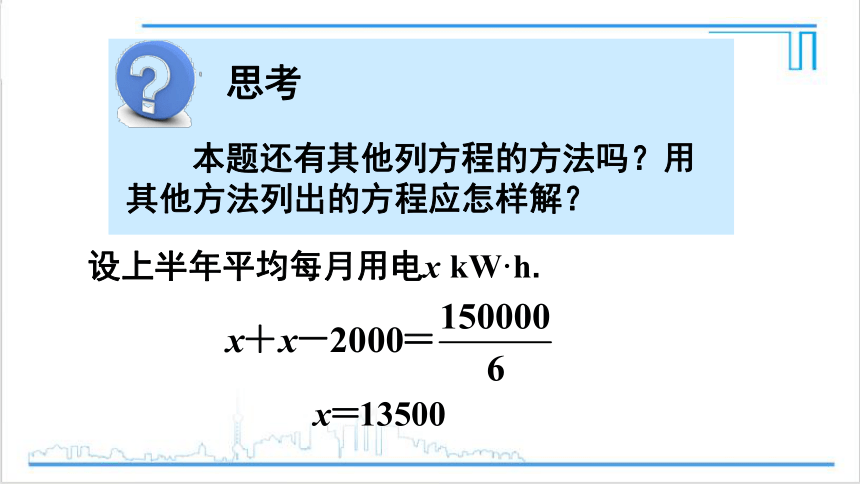
思考
本题还有其他列方程的方法吗?用其他方法列出的方程应怎样解?
设上半年平均每月用电x kW·h.
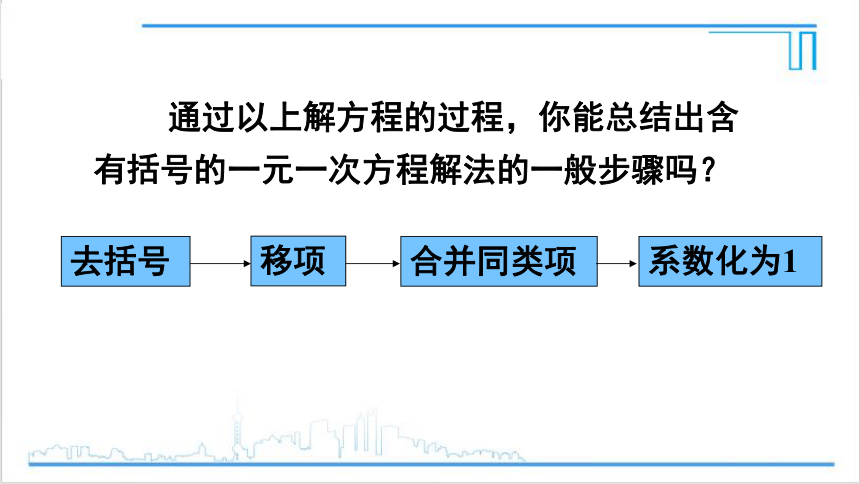
通过以上解方程的过程,你能总结出含有括号的一元一次方程解法的一般步骤吗?
去括号
移项
合并同类项
系数化为1
例1 解下列方程:
(1)2x –(x + 10)= 5x + 2(x – 1);
解:去括号,得
2x – x – 10 = 5x +2x – 2.
移项,得
2x – x – 5x – 2x = – 2 + 10.
合并同类项,得
– 6x = 8.
系数化为1,得
(2)3x – 7(x – 1)= 3 – 2(x + 3).
解:去括号,得
移项,得
合并同类项,得
–2x = –10.
系数化为1,得
3x – 7x + 7= 3 – 2x – 6.
3x – 7x + 2x= 3 – 6 – 7.
x = 5.
练习1 期中数学考试后,小明、小方和小华三名同学对答案,其中有一道题三人答案各不相同,每个人都认为自己做得对,你能帮他们看看到底谁做得对吗?做错的同学又是错在哪儿呢?
题目:一个两位数,个位上的数是2,十位上的数是x,把2和x对调,新两位数的2倍还比原两位数小18,你能求出x是几吗?
巩固练习
小方:
解:(10x + 2) – 2(x + 20)= 18
去括号,得10x + 2 – 2x – 20 = 18
合并同类项,得 8x = 40
移项,得10x – 2x = 18 + 20 + 2
系数化为1,得x = 5
去括号错
移项错
小华:
解:(10x + 2) – 2(x + 20)= 18
去括号,得10x + 2 – 2x – 40 = 18
合并同类项,得 8x = 60
移项,得10x – 2x = 18 + 40 + 2
系数化为1,得x = 7.5
移项错
小明:
解: 2(x + 20)– (10x + 2) = 18
去括号,得2x + 40 – 10x – 2 = 18
合并同类项,得 –8x = – 20
移项,得 2x – 10x = 18 – 40 + 2
系数化为1,得x = 2.5
方程列错
例2 一艘船从甲码头到乙码头顺流而行,用了2 h;从乙码头返回甲码头逆流而行,用了2.5 h.已知水流的速度是3 km/h,求船在静水中的速度.
分析:
一般情况下可以认为这艘船往返的路程相等, 顺流速度__顺流时间__逆流速度__逆流时间 .
=
×
×
解:设船在静水中的平均速度为x km/h,则顺流
的速度为(x+3) km/h,逆流速度为(x-3) km/h.
根据往返路程相等,列得
去括号,得
移项及合并同类项,得
系数化为1,得
答:船在静水中的平均速度为 27 km/h.
2(x + 3)= 2.5(x – 3).
2x + 6 = 2.5x – 7.5.
0.5x = 13.5.
x = 27.
巩固练习
练习2 解下列方程
解:去括号,得 2x + 6 = 5x.
移项,得 2x – 5x = –6.
合并同类项,得 –3x = –6.
系数化为1,得 x = 2.
(1)2(x + 3)= 5x
【课本P95 练习】
解:去括号,得
移项,得
合并同类项,得 11x = 17
系数化为1,得 x =
(2)4x + 3(2x – 3)= 12 – ( x + 4)
4x + 6x – 9= 12 – x – 4
4x + 6x + x = 12 – 4 + 9
【课本P95 练习】
解:去括号,得
移项,得
合并同类项,得
系数化为1,得
(3)
【课本P95 练习】
解:去括号,得
移项,得
合并同类项,得 – 2x = 0
系数化为1,得 x = 0
(4)2 – 3(x + 1)= 1 – 2( 1 + 0.5x )
2 – 3x – 3= 1 – 2 – x
– 3x + x= 1 – 2 – 2 + 3
【课本P95 练习】
随堂演练
基础巩固
1. 对方程 25b – (b – 5)= 29 去括号,得________________,移项,得_______________,合并同类项,得_________,系数化为1,得_______.
25b – b + 5 = 29
25b – b = 29 – 5
24b = 24
b = 1
综合应用
2. 买两种布料共138米,花了540元.其中蓝布料每米3元,黑布料每米5元,两种布料各买了多少米?
解:设蓝布料买了x米,则黑布料买了(138-x)米.
列方程得 3x + 5(138 – x) = 540.
去括号,得 3x + 690 – 5x = 540.
移项,得 3x – 5x = 540 – 690.
合并同类项,得 – 2x = – 150.
系数化为1,得 x = 75.
138 – x = 138 – 75 = 63
答:蓝布料买了75米,黑布料买了63米.
拓展延伸
3.x为何值时,式子 与 的值相等?
解:由题意得
去括号,得
移项、合并同类项,得 –x = 8
系数化为1,得x = –8
课堂小结
6x+6(x-2 000)=150 000
6x+6x-12 000=150 000
6x+6x=150 000+12 000
12x=162 000
x=13 500
去括号
合并同类项
移项
系数化为1
课后作业
1.从课后习题中选取;
2.完成练习册本课时的习题.
第1课时 去括号
R·七年级上册
3.3 解一元一次方程(二)
——去括号与去分母
新课导入
导入课题
前面我们已经学习了运用移项、合并同类项的方法解一元一次方程.对于像2(x–3)+3(x–1)=5这样的方程,又该怎么办呢?今天我们来学习含有括号的一元一次方程的解法.
学习目标
(1)会用去括号的方法解一元一次方程,进一步体会等式变形中的化归思想.
(2)进一步熟悉如何设未知数列方程解应用题,体会方程思想在解决实际问题的作用.
推进新课
知识点1
去括号
问题1
某工厂加强节能措施,去年下半年与上半年相比,月平均用电量减少2 000 kW·h(千瓦·时),全年用电15 万 kW·h.这个工厂去年上半年每月平均用电是多少?
月平均用电量×n(月数)=n个月用电量
温馨提示:
1 kW·h的电量是指1 kW的电器1 h的用电量.
分析:设上半年每月平均用电x kW·h,则下半年每月平均用电为(x-2000) kW·h.上半年共用电6x kW·h;下半年共用电6(x-2000) kW·h.
6x+6(x -2 000)=150 000
根据题意列出方程
怎样解这个方程?
这个方程与我们前面
研究过的方程有什么
不同?
6x+6(x-2 000)=150 000
6x+6x-12 000=150 000
6x+6x=150 000+12 000
12x=162 000
x=13 500
去括号
合并同类项
移项
系数化为1
思考
本题还有其他列方程的方法吗?用其他方法列出的方程应怎样解?
设上半年平均每月用电x kW·h.
通过以上解方程的过程,你能总结出含有括号的一元一次方程解法的一般步骤吗?
去括号
移项
合并同类项
系数化为1
例1 解下列方程:
(1)2x –(x + 10)= 5x + 2(x – 1);
解:去括号,得
2x – x – 10 = 5x +2x – 2.
移项,得
2x – x – 5x – 2x = – 2 + 10.
合并同类项,得
– 6x = 8.
系数化为1,得
(2)3x – 7(x – 1)= 3 – 2(x + 3).
解:去括号,得
移项,得
合并同类项,得
–2x = –10.
系数化为1,得
3x – 7x + 7= 3 – 2x – 6.
3x – 7x + 2x= 3 – 6 – 7.
x = 5.
练习1 期中数学考试后,小明、小方和小华三名同学对答案,其中有一道题三人答案各不相同,每个人都认为自己做得对,你能帮他们看看到底谁做得对吗?做错的同学又是错在哪儿呢?
题目:一个两位数,个位上的数是2,十位上的数是x,把2和x对调,新两位数的2倍还比原两位数小18,你能求出x是几吗?
巩固练习
小方:
解:(10x + 2) – 2(x + 20)= 18
去括号,得10x + 2 – 2x – 20 = 18
合并同类项,得 8x = 40
移项,得10x – 2x = 18 + 20 + 2
系数化为1,得x = 5
去括号错
移项错
小华:
解:(10x + 2) – 2(x + 20)= 18
去括号,得10x + 2 – 2x – 40 = 18
合并同类项,得 8x = 60
移项,得10x – 2x = 18 + 40 + 2
系数化为1,得x = 7.5
移项错
小明:
解: 2(x + 20)– (10x + 2) = 18
去括号,得2x + 40 – 10x – 2 = 18
合并同类项,得 –8x = – 20
移项,得 2x – 10x = 18 – 40 + 2
系数化为1,得x = 2.5
方程列错
例2 一艘船从甲码头到乙码头顺流而行,用了2 h;从乙码头返回甲码头逆流而行,用了2.5 h.已知水流的速度是3 km/h,求船在静水中的速度.
分析:
一般情况下可以认为这艘船往返的路程相等, 顺流速度__顺流时间__逆流速度__逆流时间 .
=
×
×
解:设船在静水中的平均速度为x km/h,则顺流
的速度为(x+3) km/h,逆流速度为(x-3) km/h.
根据往返路程相等,列得
去括号,得
移项及合并同类项,得
系数化为1,得
答:船在静水中的平均速度为 27 km/h.
2(x + 3)= 2.5(x – 3).
2x + 6 = 2.5x – 7.5.
0.5x = 13.5.
x = 27.
巩固练习
练习2 解下列方程
解:去括号,得 2x + 6 = 5x.
移项,得 2x – 5x = –6.
合并同类项,得 –3x = –6.
系数化为1,得 x = 2.
(1)2(x + 3)= 5x
【课本P95 练习】
解:去括号,得
移项,得
合并同类项,得 11x = 17
系数化为1,得 x =
(2)4x + 3(2x – 3)= 12 – ( x + 4)
4x + 6x – 9= 12 – x – 4
4x + 6x + x = 12 – 4 + 9
【课本P95 练习】
解:去括号,得
移项,得
合并同类项,得
系数化为1,得
(3)
【课本P95 练习】
解:去括号,得
移项,得
合并同类项,得 – 2x = 0
系数化为1,得 x = 0
(4)2 – 3(x + 1)= 1 – 2( 1 + 0.5x )
2 – 3x – 3= 1 – 2 – x
– 3x + x= 1 – 2 – 2 + 3
【课本P95 练习】
随堂演练
基础巩固
1. 对方程 25b – (b – 5)= 29 去括号,得________________,移项,得_______________,合并同类项,得_________,系数化为1,得_______.
25b – b + 5 = 29
25b – b = 29 – 5
24b = 24
b = 1
综合应用
2. 买两种布料共138米,花了540元.其中蓝布料每米3元,黑布料每米5元,两种布料各买了多少米?
解:设蓝布料买了x米,则黑布料买了(138-x)米.
列方程得 3x + 5(138 – x) = 540.
去括号,得 3x + 690 – 5x = 540.
移项,得 3x – 5x = 540 – 690.
合并同类项,得 – 2x = – 150.
系数化为1,得 x = 75.
138 – x = 138 – 75 = 63
答:蓝布料买了75米,黑布料买了63米.
拓展延伸
3.x为何值时,式子 与 的值相等?
解:由题意得
去括号,得
移项、合并同类项,得 –x = 8
系数化为1,得x = –8
课堂小结
6x+6(x-2 000)=150 000
6x+6x-12 000=150 000
6x+6x=150 000+12 000
12x=162 000
x=13 500
去括号
合并同类项
移项
系数化为1
课后作业
1.从课后习题中选取;
2.完成练习册本课时的习题.
