函数的最值与导数
图片预览





文档简介
课件15张PPT。函数的最值与导数(1)极值是一个局部概念,反映了函数在某一点附近的大小情况;(2)极值点是自变量的值,极值指的是函数值;(3)函数的极大(小)值可能不止一个,而且函数的极大值未必大于极小值;【关于极值概念的几点说明】(4)函数的极值点一定在区间的内部,区间的端点不能成为极值点。而函数的最值既可能在区间的内部取得,也可能在区间的端点取得。(1)如果f /(x0)=0, 并且在x0附近的左侧 f /(x)>0
右侧f /(x)<0, 那么f(x0)是极大值【函数的极值与导数的关系】(2)如果f /(x0)=0, 并且在x0附近的左侧 f /(x)<0
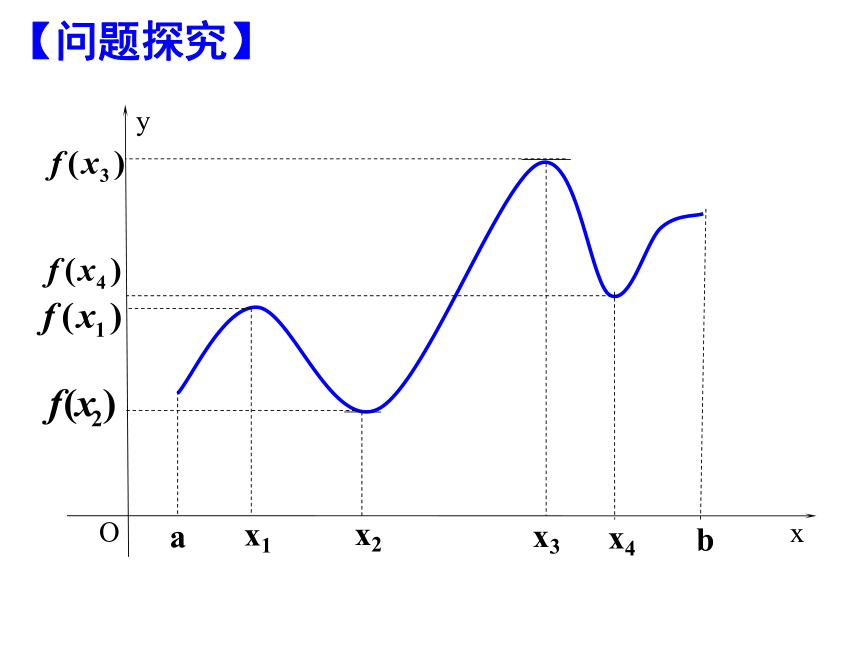
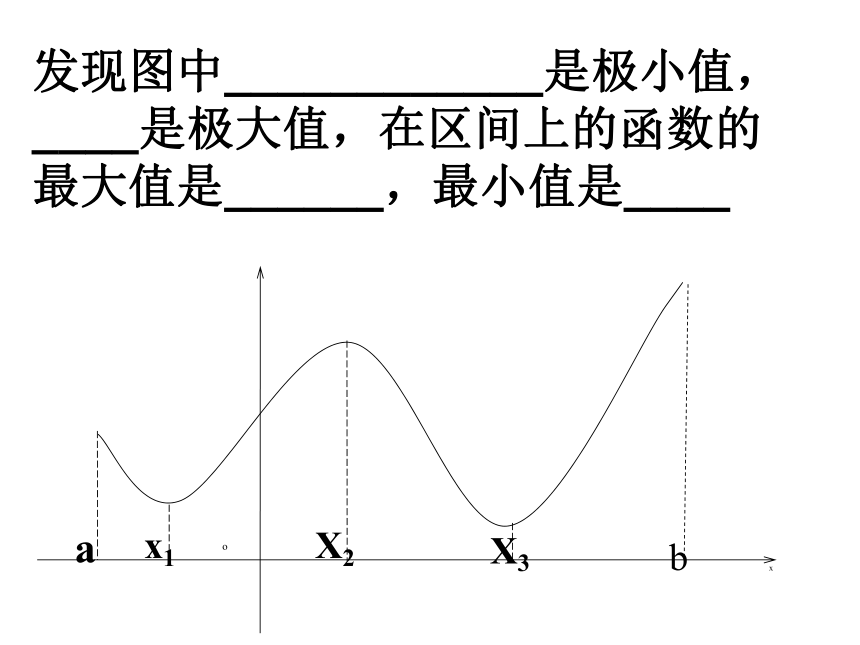
右侧f /(x)>0, 那么f(x0)是极小值【问题探究】 在某些问题中,往往关心的是函数在整个定义域区间上,哪个值最大或最小的问题,这就是我们通常所说的最值问题. 发现图中____________是极小值,
____是极大值,在区间上的函数的
最大值是______,最小值是____ (2)将y=f(x)的各极值与f(a)、f(b)比较,其中最大的一个为最大值,最小的一个最小值 求f(x)在闭区间[a,b]上的最值的步骤:(1)求f(x)在区间(a,b)内极值(极大值或极小值)表格法例1、求函数f(x)=x2-4x+6在区间[1,5]内
的最大值和最小值 法一 、 将二次函数f(x)=x2-4x+6配方,利用二次函数单调性处理
例1、求函数f(x)=x2-4x+6在区间[1,5]内
的极值与最值 故函数f(x) 在区间[1,5]内的最大值为11,最小值为2 法二、解、 f ’(x)=2x-4令f ’(x)=0,即2x-4=0,得x=2-+3112例2、求函数 在区间
上的最大值与最小值。 从上表知,当 时,函数有最大值13,当 时,函数有最小值4解:先求导数得,列表如下练习:课本第33页第2题与第3题作业:34页第4题
右侧f /(x)<0, 那么f(x0)是极大值【函数的极值与导数的关系】(2)如果f /(x0)=0, 并且在x0附近的左侧 f /(x)<0
右侧f /(x)>0, 那么f(x0)是极小值【问题探究】 在某些问题中,往往关心的是函数在整个定义域区间上,哪个值最大或最小的问题,这就是我们通常所说的最值问题. 发现图中____________是极小值,
____是极大值,在区间上的函数的
最大值是______,最小值是____ (2)将y=f(x)的各极值与f(a)、f(b)比较,其中最大的一个为最大值,最小的一个最小值 求f(x)在闭区间[a,b]上的最值的步骤:(1)求f(x)在区间(a,b)内极值(极大值或极小值)表格法例1、求函数f(x)=x2-4x+6在区间[1,5]内
的最大值和最小值 法一 、 将二次函数f(x)=x2-4x+6配方,利用二次函数单调性处理
例1、求函数f(x)=x2-4x+6在区间[1,5]内
的极值与最值 故函数f(x) 在区间[1,5]内的最大值为11,最小值为2 法二、解、 f ’(x)=2x-4令f ’(x)=0,即2x-4=0,得x=2-+3112例2、求函数 在区间
上的最大值与最小值。 从上表知,当 时,函数有最大值13,当 时,函数有最小值4解:先求导数得,列表如下练习:课本第33页第2题与第3题作业:34页第4题
