【高效备课】人教版七(上) 3.4 实际问题与一元一次方程 第1课时 配套问题与工程问题 课件
文档属性
| 名称 | 【高效备课】人教版七(上) 3.4 实际问题与一元一次方程 第1课时 配套问题与工程问题 课件 |  | |
| 格式 | pptx | ||
| 文件大小 | 355.3KB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-09-12 16:36:58 | ||
图片预览








文档简介
(共21张PPT)
第1课时 配套问题与工程问题
R·七年级上册
3.4 实际问题与一元一次方程
新课导入
导入课题
前面我们在学习一元一次方程的解法时,附带研究了如何列一元一次方程解决实际问题,初步了解了方程是分析和解决问题的一种很有用的数学工具,接下来的内容介绍了从几个典型的实际问题入手教会同学们列方程解决实际问题的具体方法.
学习目标
(1)会运用一元一次方程解决物品配套问题和工程问题.
(2)掌握用一元一次方程解决实际问题的基本思路和步骤.
推进新课
知识点1
配套问题
例1 某车间有22名工人,每人每天可以生产1 200个螺钉或2 000个螺母. 1个螺钉需要配 2个螺母,为使每天生产的螺钉和螺母刚好配套,应安排生产螺钉和螺母的工人各多少名?
分析:每天生产的螺母数量是螺钉数量的2倍时,它们刚好配套.
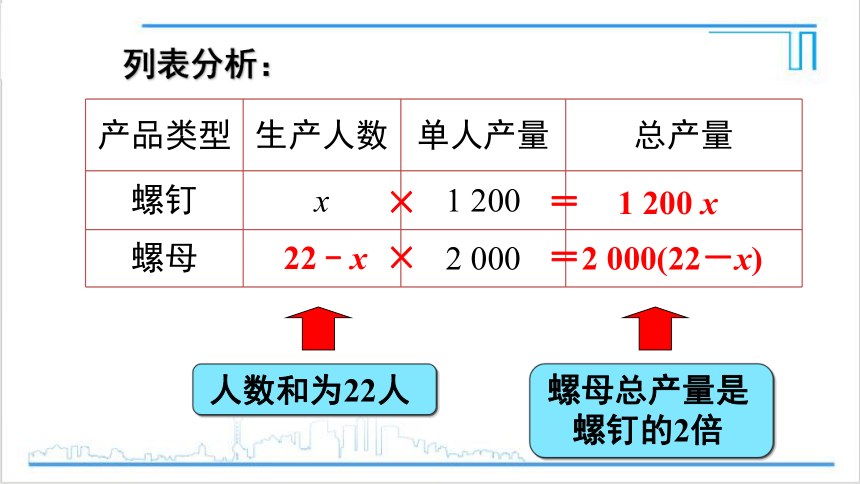
列表分析:
产品类型 生产人数 单人产量 总产量
螺钉 x 1 200
螺母 2 000
×
=
1 200 x
×
=
2 000(22-x)
人数和为22人
22﹣x
螺母总产量是螺钉的2倍
解:设应安排x名工人生产螺钉,(22-x)名工人生产螺母.
依题意得: 2 000(22-x)=2×1 200x .
解方程,得:5(22-x)=6x,
110- 5x=6x,
x=10.
22-x=12.
答:应安排10名工人生产螺钉,12名工人生产螺母.
如果设x名工人生产螺母,怎样列方程?
解:设应安排 x名工人生产螺母,(22-x)名工人生产螺钉.
依题意得: 2×1200(22-x)=2 000x .
这类问题中配套的物品之间具有一定的数量关系,这可以作为列方程的依据.
练习1 一套仪器由一个A部件和三个B部件构成. 用1 m3钢材可以做40个A部件或240个B部件. 现要用6 m3钢材制作这种仪器,应用多少钢材做A部件,多少钢材做B部件,恰好配成这种仪器多少套?
解:设应用 x m3钢材做A部件,(6-x) m3 钢材做B部件. 依题意得: 3×40 x=240 (6-x) .
解方程,得: x=4.
答:应用4 m3钢材做A部件,2 m3 钢材做B部件,配成这种仪器160套.
巩固练习
【课本P101 练习 第1题】
知识点2
工程问题
例2 整理一批图书,由一个人做要40 h 完成.现计划由一部分人先做4 h,然后增加 2人与他们一起做8 h,完成这项工作. 假设这些人的工作效率相同,具体应先安排多少人工作?
列表分析:
人均效率 人数 时间 工作量
前一部分工作 x 4
后一部分工作 x+2 8
×
=
×
×
×
=
工作量之和等于总工作量1
这类问题中常常把总工作量看作1,并利用“工作量=人均效率×人数×时间”的关系考虑问题.
解:设安排 x 人先做4 h.
依题意得: + =1
解方程,得:4x+8(x+2)=40,
4x+8x+16=40,
12x=24,
x=2.
答:应先安排 2人做4 h.
归纳
用一元一次方程解决实际问题的基本过程如下:
实际问题
实际问题的答案
一元一次方程
一元一次方程的解(x=a)
设未知数
列方程
解方程
检验
这一过程一般包括以下几个步骤:
1. 审:审题,分析题目中的数量关系;
2. 设:设适当的未知数,并表示未知量;
3. 列:根据题目中的数量关系列方程;
4. 解:解这个方程;
5. 答:检验并答话.
练习 一条地下管线由甲工程队单独铺设需要12天,由乙工程队单独铺设需要24天.如果由这两个工程队从两端同时施工,要多少天可以铺好这条管线
【课本P101 练习 第2题】
基础巩固
1. 甲队有32人,乙队有28人,现从乙队抽调x人到甲队,使甲队人数是乙队人数的2倍,依题意,列出的方程是_______________.
32+x=2(28-x)
随堂演练
2. 制作一张桌子要用一个桌面和4条桌腿,1 m3木材可制作20个桌面,或者制作 400条桌腿,现有12 m3木材,应怎样安排用料才能制作尽可能多的桌子?
解:设计划用x m3的木材制作桌面,
(12 – x) m3的木材制作桌腿.
根据题意,得4×20x = 400(12 – x),
解得 x = 10. 12 – x = 12 – 10 = 2.
答:计划用10 m3的木材制作桌面,2 m3的木材制作桌腿.
综合应用
3. 整理一批数据,由一人做需80 h完成,现计划先由一些人做2 h,再增加5人做8 h,完成这项工作的 ,怎样安排参与整理数据的具体人数?
解:设先由x人做2 h.
解得x = 2,x + 5 = 7(人)
答:先安排2人做2 h,再由7人做8 h就可以完成
这项工作的 .
拓展延伸
4. 某糕点厂中秋节前要制作一批盒装月饼,每盒中装2块大月饼和4块小月饼,制作1块大月饼要用面粉0.05 kg,制作1块小月饼要用面粉0.02 kg,现共有面粉4500 kg,制作两种月饼应各用多少面粉,才能生产最多的盒装月饼?
解:设制作大月饼用 x kg面粉,制作小月饼用(4500 – x) kg面粉,才能生产最多的盒装月饼.
解得 x = 2500,4500 – x = 4500 – 2500 = 2000.
即制作大月饼用2500 kg面粉,制作小月饼用2000 kg面粉,才能生产最多的盒装月饼.
根据题意,得
课堂小结
实际问题
实际问题的答案
一元一次方程
一元一次方程的解(x=a)
设未知数
列方程
解方程
检验
课后作业
1.从课后习题中选取;
2.完成练习册本课时的习题。
第1课时 配套问题与工程问题
R·七年级上册
3.4 实际问题与一元一次方程
新课导入
导入课题
前面我们在学习一元一次方程的解法时,附带研究了如何列一元一次方程解决实际问题,初步了解了方程是分析和解决问题的一种很有用的数学工具,接下来的内容介绍了从几个典型的实际问题入手教会同学们列方程解决实际问题的具体方法.
学习目标
(1)会运用一元一次方程解决物品配套问题和工程问题.
(2)掌握用一元一次方程解决实际问题的基本思路和步骤.
推进新课
知识点1
配套问题
例1 某车间有22名工人,每人每天可以生产1 200个螺钉或2 000个螺母. 1个螺钉需要配 2个螺母,为使每天生产的螺钉和螺母刚好配套,应安排生产螺钉和螺母的工人各多少名?
分析:每天生产的螺母数量是螺钉数量的2倍时,它们刚好配套.
列表分析:
产品类型 生产人数 单人产量 总产量
螺钉 x 1 200
螺母 2 000
×
=
1 200 x
×
=
2 000(22-x)
人数和为22人
22﹣x
螺母总产量是螺钉的2倍
解:设应安排x名工人生产螺钉,(22-x)名工人生产螺母.
依题意得: 2 000(22-x)=2×1 200x .
解方程,得:5(22-x)=6x,
110- 5x=6x,
x=10.
22-x=12.
答:应安排10名工人生产螺钉,12名工人生产螺母.
如果设x名工人生产螺母,怎样列方程?
解:设应安排 x名工人生产螺母,(22-x)名工人生产螺钉.
依题意得: 2×1200(22-x)=2 000x .
这类问题中配套的物品之间具有一定的数量关系,这可以作为列方程的依据.
练习1 一套仪器由一个A部件和三个B部件构成. 用1 m3钢材可以做40个A部件或240个B部件. 现要用6 m3钢材制作这种仪器,应用多少钢材做A部件,多少钢材做B部件,恰好配成这种仪器多少套?
解:设应用 x m3钢材做A部件,(6-x) m3 钢材做B部件. 依题意得: 3×40 x=240 (6-x) .
解方程,得: x=4.
答:应用4 m3钢材做A部件,2 m3 钢材做B部件,配成这种仪器160套.
巩固练习
【课本P101 练习 第1题】
知识点2
工程问题
例2 整理一批图书,由一个人做要40 h 完成.现计划由一部分人先做4 h,然后增加 2人与他们一起做8 h,完成这项工作. 假设这些人的工作效率相同,具体应先安排多少人工作?
列表分析:
人均效率 人数 时间 工作量
前一部分工作 x 4
后一部分工作 x+2 8
×
=
×
×
×
=
工作量之和等于总工作量1
这类问题中常常把总工作量看作1,并利用“工作量=人均效率×人数×时间”的关系考虑问题.
解:设安排 x 人先做4 h.
依题意得: + =1
解方程,得:4x+8(x+2)=40,
4x+8x+16=40,
12x=24,
x=2.
答:应先安排 2人做4 h.
归纳
用一元一次方程解决实际问题的基本过程如下:
实际问题
实际问题的答案
一元一次方程
一元一次方程的解(x=a)
设未知数
列方程
解方程
检验
这一过程一般包括以下几个步骤:
1. 审:审题,分析题目中的数量关系;
2. 设:设适当的未知数,并表示未知量;
3. 列:根据题目中的数量关系列方程;
4. 解:解这个方程;
5. 答:检验并答话.
练习 一条地下管线由甲工程队单独铺设需要12天,由乙工程队单独铺设需要24天.如果由这两个工程队从两端同时施工,要多少天可以铺好这条管线
【课本P101 练习 第2题】
基础巩固
1. 甲队有32人,乙队有28人,现从乙队抽调x人到甲队,使甲队人数是乙队人数的2倍,依题意,列出的方程是_______________.
32+x=2(28-x)
随堂演练
2. 制作一张桌子要用一个桌面和4条桌腿,1 m3木材可制作20个桌面,或者制作 400条桌腿,现有12 m3木材,应怎样安排用料才能制作尽可能多的桌子?
解:设计划用x m3的木材制作桌面,
(12 – x) m3的木材制作桌腿.
根据题意,得4×20x = 400(12 – x),
解得 x = 10. 12 – x = 12 – 10 = 2.
答:计划用10 m3的木材制作桌面,2 m3的木材制作桌腿.
综合应用
3. 整理一批数据,由一人做需80 h完成,现计划先由一些人做2 h,再增加5人做8 h,完成这项工作的 ,怎样安排参与整理数据的具体人数?
解:设先由x人做2 h.
解得x = 2,x + 5 = 7(人)
答:先安排2人做2 h,再由7人做8 h就可以完成
这项工作的 .
拓展延伸
4. 某糕点厂中秋节前要制作一批盒装月饼,每盒中装2块大月饼和4块小月饼,制作1块大月饼要用面粉0.05 kg,制作1块小月饼要用面粉0.02 kg,现共有面粉4500 kg,制作两种月饼应各用多少面粉,才能生产最多的盒装月饼?
解:设制作大月饼用 x kg面粉,制作小月饼用(4500 – x) kg面粉,才能生产最多的盒装月饼.
解得 x = 2500,4500 – x = 4500 – 2500 = 2000.
即制作大月饼用2500 kg面粉,制作小月饼用2000 kg面粉,才能生产最多的盒装月饼.
根据题意,得
课堂小结
实际问题
实际问题的答案
一元一次方程
一元一次方程的解(x=a)
设未知数
列方程
解方程
检验
课后作业
1.从课后习题中选取;
2.完成练习册本课时的习题。
