【高效备课】人教版七(上) 4.2 直线、射线、线段 第2课时 线段的比较与度量 课件
文档属性
| 名称 | 【高效备课】人教版七(上) 4.2 直线、射线、线段 第2课时 线段的比较与度量 课件 |

|
|
| 格式 | pptx | ||
| 文件大小 | 412.7KB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-09-12 16:36:58 | ||
图片预览






文档简介
(共24张PPT)
4.2 直线、射线、线段
第2课时 线段的比较与度量
R·七年级上册
新课导入
上节课我们学习了直线、射线、线段的概念和表示方法,这节课来学习线段的大小比较,线段的和、差、倍、分.
学习目标
(1)掌握线段的大小比较方法,会比较线段的大小.
(2)理解线段的和、差、倍、分的意义,并会用几何语言描述它们.
(3)掌握画一条线段等于已知线段的画图方法,并能完成其他相关线段的画图.
推进新课
作线段等于已知线段
知识点1
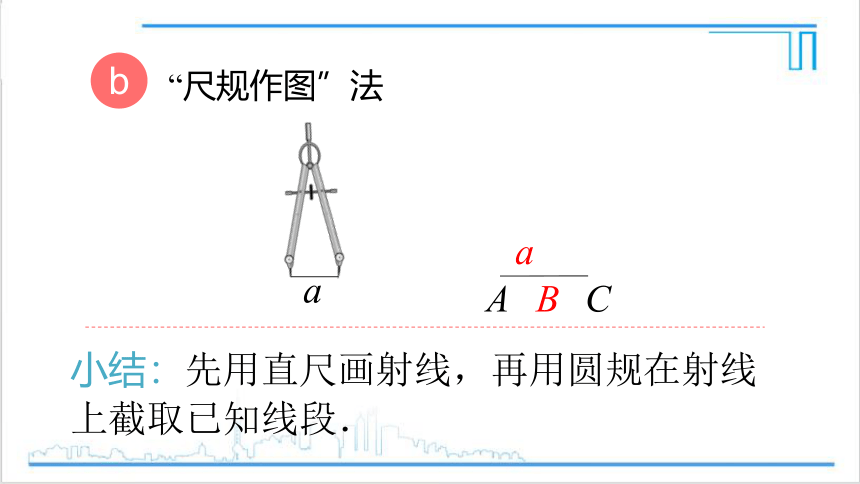
问题 如图,已知线段a,你可以画出一条同样大小的线段来吗?用什么方法呢?
a
a
度量法:用刻度尺量出已知线段,再画一条与它相等的线段.
a
A C
a
B
b
“尺规作图”法
小结:先用直尺画射线,再用圆规在射线上截取已知线段.
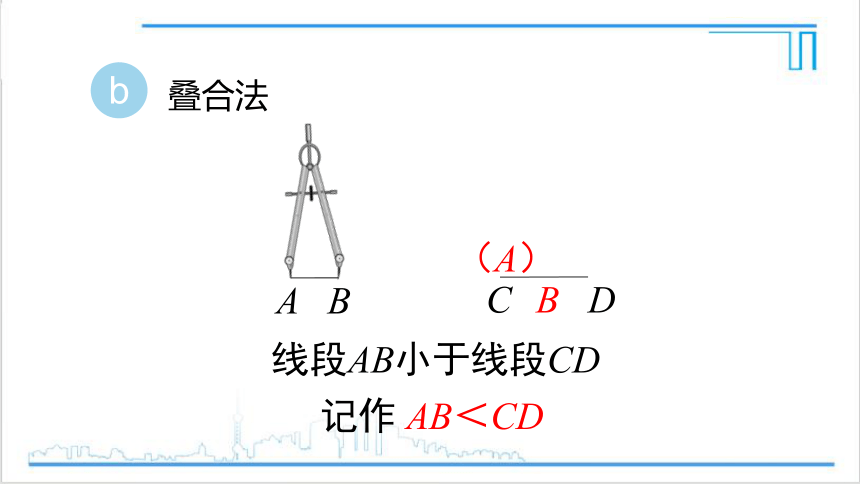
问题 黑板上有两条线段,你能判断一下它们的长短吗?你用的什么方法?
a
度量法:即用刻度尺分别量出它们的长度,然后比较它们的长度的大小.
a
b
A B
C D
(A)
B
b
叠合法
记作 AB<CD
线段AB小于线段CD
1
2
两条线段要放在同一条直线上.
一个端点重合,另一个端点要放在公共端点的同侧.
用叠合法比较线段的长短时,有什么需要注意的吗?
思考
强化练习
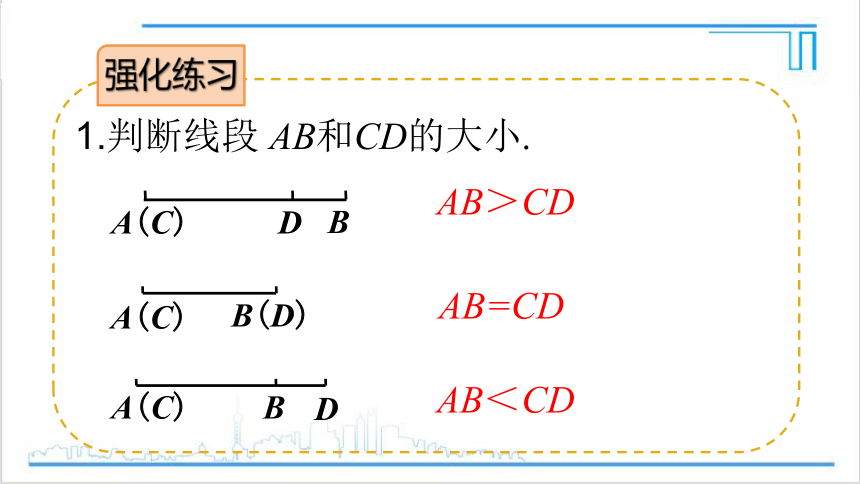
1.判断线段 AB和CD的大小.
AB>CD
A(C)
D
B
A(C)
B
D
A(C)
B(D)
AB=CD
AB<CD
两条线段的和、差、倍、分
知识点2
问题 如图,已知线段 a 和 b,且 a>b.
a
b
a. AB=a,BC=b,则线段AC就是a与b的 .
记作 .
A B C
和
AC=a+b
问题 如图,已知线段 a 和 b,且 a>b.
a
b
b. AB=a,BD=b,则线段AD就是a与b的 .
记作 .
A B
差
AD=a-b
D
问题 如图,已知线段a和线段b,怎样通过作图得到a与b的和、a与b的差呢?
b
a
B
C
a
b
A
P
B
C
a
b
A
P
AC=a+b
CB=a-b
问题 如图,已知线段a,求作线段AC=2a.
a
M
C
a
A
P
AC=2a
a
思考 线段AC的中点是什么?
M
C
a
A
P
a
点 M 把线段 AC 分成相等的两条线段AM与MC,点 M 叫做线段 AC 的中点,可知 AM=MC= AC.
1
2
思考 那么什么叫做三等分点?四等分点呢?
a
三等分点
如图,若点M、N是线段AB的三等分点,
则AM = = = ,反过来也成立.
MN
NB
AB
1
3
b
四等分点
如图,若点M、N、P是线段AB的四等分
点,则AM = = = = ,反过来也成立.
MN
NP
AB
1
4
PB
强化练习
1.如图,点 D 是线段 AB 的中点,C 是线段 AD的中点,若 AB =4cm,求线段 CD 的长度.
【课本P128 练习 第3题】
【课本P128 练习 第2题】
随堂演练
1. 如图,已知线段a,b,作一条线段,使它等于2a-b.
解:作射线AB,在射线AB上截取线段AC=2a,在线段CA上截取线段CE=b,则线段AE为求作的线段.
2. 如图,已知线段a、b、c,用圆规和直尺作线段,使它等于a+2b-c.
解:作射线AB,在射线AB上截取线段AC=a+
2b,在线段CA上截取线段CE=c,则线段AE为求作的线段.
【课本P128 练习 第1题】
3. 估计下列图中线段AB与线段AC的大小关系,再用刻度尺或用圆规来检验你的估计.
2.两条直线相交,有一个交点,三条直线相交最多有多少个交点?四条直线呢?你能发现什么规律吗?
1
3=1+2
6=1+2+3
解:三条直线相交最多有1+2=3个交点,四条直线相交最多有1+2+3=6个交点,我们可以发现,n条直线相交最多有(1+2+3+4+
……+n-1)个交点,也就是 个交点,此处n≥3且n为自然数.
课堂小结
线段的比较
两条线段的和、差、倍、分
度量法
叠合法
1.从课后习题中选取;
2.完成练习册本课时的习题。
课后作业
4.2 直线、射线、线段
第2课时 线段的比较与度量
R·七年级上册
新课导入
上节课我们学习了直线、射线、线段的概念和表示方法,这节课来学习线段的大小比较,线段的和、差、倍、分.
学习目标
(1)掌握线段的大小比较方法,会比较线段的大小.
(2)理解线段的和、差、倍、分的意义,并会用几何语言描述它们.
(3)掌握画一条线段等于已知线段的画图方法,并能完成其他相关线段的画图.
推进新课
作线段等于已知线段
知识点1
问题 如图,已知线段a,你可以画出一条同样大小的线段来吗?用什么方法呢?
a
a
度量法:用刻度尺量出已知线段,再画一条与它相等的线段.
a
A C
a
B
b
“尺规作图”法
小结:先用直尺画射线,再用圆规在射线上截取已知线段.
问题 黑板上有两条线段,你能判断一下它们的长短吗?你用的什么方法?
a
度量法:即用刻度尺分别量出它们的长度,然后比较它们的长度的大小.
a
b
A B
C D
(A)
B
b
叠合法
记作 AB<CD
线段AB小于线段CD
1
2
两条线段要放在同一条直线上.
一个端点重合,另一个端点要放在公共端点的同侧.
用叠合法比较线段的长短时,有什么需要注意的吗?
思考
强化练习
1.判断线段 AB和CD的大小.
AB>CD
A(C)
D
B
A(C)
B
D
A(C)
B(D)
AB=CD
AB<CD
两条线段的和、差、倍、分
知识点2
问题 如图,已知线段 a 和 b,且 a>b.
a
b
a. AB=a,BC=b,则线段AC就是a与b的 .
记作 .
A B C
和
AC=a+b
问题 如图,已知线段 a 和 b,且 a>b.
a
b
b. AB=a,BD=b,则线段AD就是a与b的 .
记作 .
A B
差
AD=a-b
D
问题 如图,已知线段a和线段b,怎样通过作图得到a与b的和、a与b的差呢?
b
a
B
C
a
b
A
P
B
C
a
b
A
P
AC=a+b
CB=a-b
问题 如图,已知线段a,求作线段AC=2a.
a
M
C
a
A
P
AC=2a
a
思考 线段AC的中点是什么?
M
C
a
A
P
a
点 M 把线段 AC 分成相等的两条线段AM与MC,点 M 叫做线段 AC 的中点,可知 AM=MC= AC.
1
2
思考 那么什么叫做三等分点?四等分点呢?
a
三等分点
如图,若点M、N是线段AB的三等分点,
则AM = = = ,反过来也成立.
MN
NB
AB
1
3
b
四等分点
如图,若点M、N、P是线段AB的四等分
点,则AM = = = = ,反过来也成立.
MN
NP
AB
1
4
PB
强化练习
1.如图,点 D 是线段 AB 的中点,C 是线段 AD的中点,若 AB =4cm,求线段 CD 的长度.
【课本P128 练习 第3题】
【课本P128 练习 第2题】
随堂演练
1. 如图,已知线段a,b,作一条线段,使它等于2a-b.
解:作射线AB,在射线AB上截取线段AC=2a,在线段CA上截取线段CE=b,则线段AE为求作的线段.
2. 如图,已知线段a、b、c,用圆规和直尺作线段,使它等于a+2b-c.
解:作射线AB,在射线AB上截取线段AC=a+
2b,在线段CA上截取线段CE=c,则线段AE为求作的线段.
【课本P128 练习 第1题】
3. 估计下列图中线段AB与线段AC的大小关系,再用刻度尺或用圆规来检验你的估计.
2.两条直线相交,有一个交点,三条直线相交最多有多少个交点?四条直线呢?你能发现什么规律吗?
1
3=1+2
6=1+2+3
解:三条直线相交最多有1+2=3个交点,四条直线相交最多有1+2+3=6个交点,我们可以发现,n条直线相交最多有(1+2+3+4+
……+n-1)个交点,也就是 个交点,此处n≥3且n为自然数.
课堂小结
线段的比较
两条线段的和、差、倍、分
度量法
叠合法
1.从课后习题中选取;
2.完成练习册本课时的习题。
课后作业
