【高效备课】人教版七(上) 4.2 直线、射线、线段 第3课时 线段的性质及其应用 课件
文档属性
| 名称 | 【高效备课】人教版七(上) 4.2 直线、射线、线段 第3课时 线段的性质及其应用 课件 |

|
|
| 格式 | pptx | ||
| 文件大小 | 370.1KB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-09-12 16:36:58 | ||
图片预览


文档简介
(共16张PPT)
4.2 直线、射线、线段
第3课时 线段的性质及其应用
R·七年级上册
新课导入
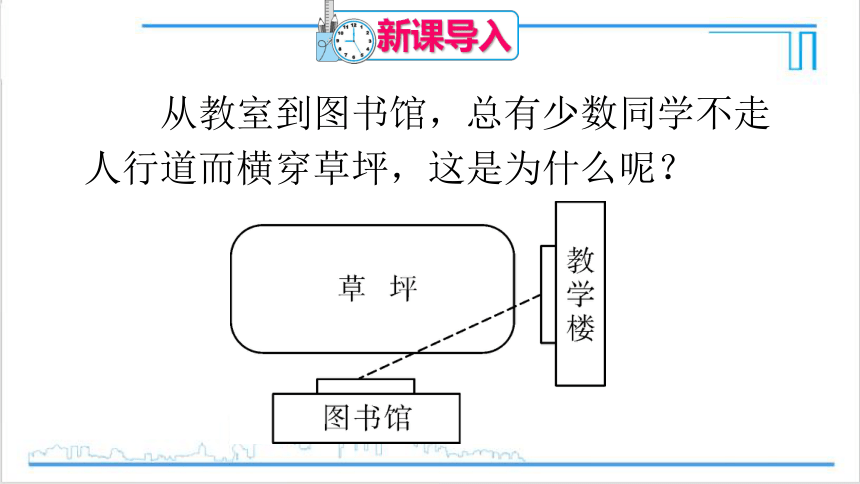
从教室到图书馆,总有少数同学不走人行道而横穿草坪,这是为什么呢?
两点之间,线段最短.
为什么两点之间线段最短呢?本课我们继续探讨线段的有关性质.
学习目标
知道“两点之间,线段最短”的性质及“两点间的距离”的意义.
推进新课
线段的性质及其应用
知识点
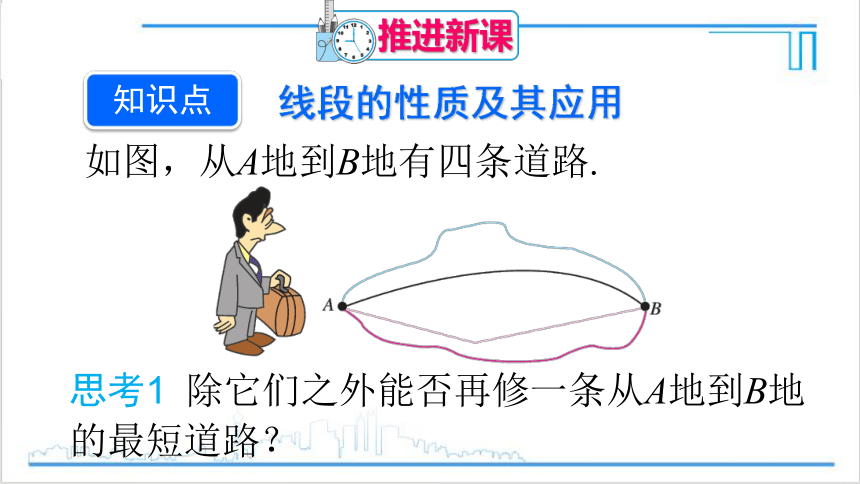
如图,从A地到B地有四条道路.
思考1 除它们之外能否再修一条从A地到B地的最短道路?
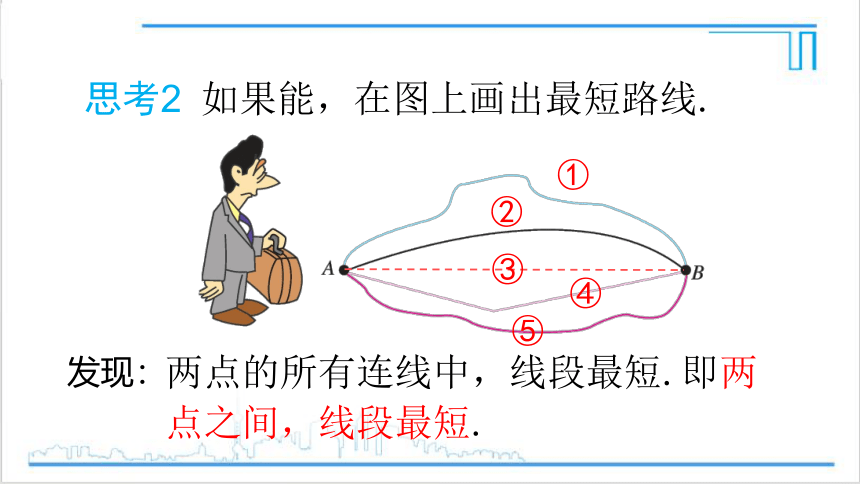
思考2 如果能,在图上画出最短路线.
两点的所有连线中,线段最短.即两点之间,线段最短.
发现:
①
②
③
④
⑤
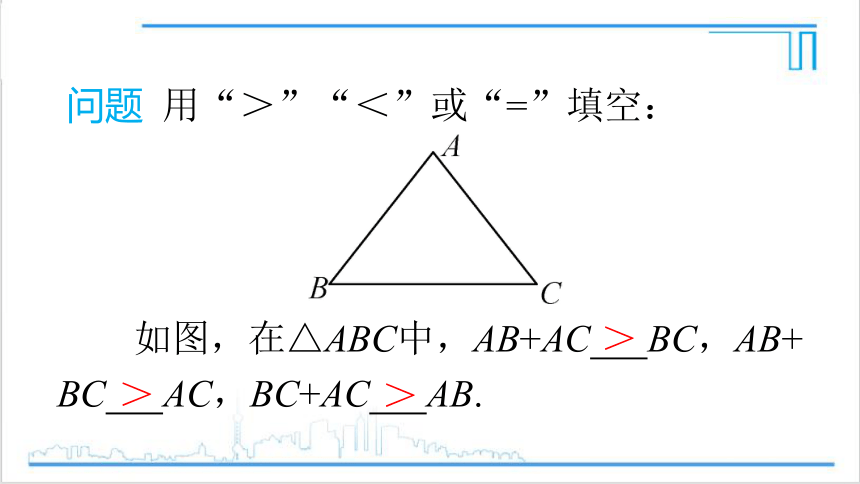
问题 用“>”“<”或“=”填空:
如图,在△ABC中,AB+AC BC,AB+
BC AC,BC+AC AB.
>
>
>
问题 你能举例说明“两点之间,线段最短”的实际应用吗?与同学们交流一下.
1
道路会尽可能修直一点.
3
人们为了走捷径,有时会横穿马路.
2
小狗看见骨头会径直跑过去.
连接两点间的线段的长度,叫做这两点的距离.
问题 A、B两点之间的距离是多少?
A
B
小结
×
×
线段AB的长度
强化练习
1.把弯曲的河道改直,能够缩短航程,这
样做的道理是( )
A.两点之间,射线最短
B.两点确定一条直线
C.两点之间,线段最短
D.两点之间,直线最短
C
强化练习
2.如图,从A出发到B时,最近的路是( )
A. A→C→D→B
B. A→C→F→E→B
C. A→C→E→B
D. A→C→G→B
C
随堂演练
1.已知A、B、C三点在同一直线上,如果
线段AB=6 cm,BC=3 cm,A、C两点的
距离为d,那么( )
A.d=9cm B.d=3cm
C.d=9cm或d=3cm D.d大小不确定
C
2.如图,一只蚂蚁要从正方体的一个顶点A沿表面爬行到顶点B,怎样爬行路线最短?如果要爬行到顶点C呢?说出你的理由.
沿AB连线爬行最短.
解:如果要爬行到顶点C,有三种
情况:若蚂蚁爬行时经过面AD,
可将这个正方体展开,在展开图
上连接AC,与棱a(或b)交于D1(或
D2),蚂蚁沿AD1→D1C(或AD2→D2C)爬行,路线最短.类似地,蚂蚁经过面AB和AE爬行到顶点C,也分别有两条最短路线,因此,蚂蚁爬行的最短路线有6条.
课堂小结
两点的所有连线中,线段最短.即两点之间,线段最短.
连接两点间的线段的长度,叫做这两点的距离.
1.从课后习题中选取;
2.完成练习册本课时的习题。
课后作业
4.2 直线、射线、线段
第3课时 线段的性质及其应用
R·七年级上册
新课导入
从教室到图书馆,总有少数同学不走人行道而横穿草坪,这是为什么呢?
两点之间,线段最短.
为什么两点之间线段最短呢?本课我们继续探讨线段的有关性质.
学习目标
知道“两点之间,线段最短”的性质及“两点间的距离”的意义.
推进新课
线段的性质及其应用
知识点
如图,从A地到B地有四条道路.
思考1 除它们之外能否再修一条从A地到B地的最短道路?
思考2 如果能,在图上画出最短路线.
两点的所有连线中,线段最短.即两点之间,线段最短.
发现:
①
②
③
④
⑤
问题 用“>”“<”或“=”填空:
如图,在△ABC中,AB+AC BC,AB+
BC AC,BC+AC AB.
>
>
>
问题 你能举例说明“两点之间,线段最短”的实际应用吗?与同学们交流一下.
1
道路会尽可能修直一点.
3
人们为了走捷径,有时会横穿马路.
2
小狗看见骨头会径直跑过去.
连接两点间的线段的长度,叫做这两点的距离.
问题 A、B两点之间的距离是多少?
A
B
小结
×
×
线段AB的长度
强化练习
1.把弯曲的河道改直,能够缩短航程,这
样做的道理是( )
A.两点之间,射线最短
B.两点确定一条直线
C.两点之间,线段最短
D.两点之间,直线最短
C
强化练习
2.如图,从A出发到B时,最近的路是( )
A. A→C→D→B
B. A→C→F→E→B
C. A→C→E→B
D. A→C→G→B
C
随堂演练
1.已知A、B、C三点在同一直线上,如果
线段AB=6 cm,BC=3 cm,A、C两点的
距离为d,那么( )
A.d=9cm B.d=3cm
C.d=9cm或d=3cm D.d大小不确定
C
2.如图,一只蚂蚁要从正方体的一个顶点A沿表面爬行到顶点B,怎样爬行路线最短?如果要爬行到顶点C呢?说出你的理由.
沿AB连线爬行最短.
解:如果要爬行到顶点C,有三种
情况:若蚂蚁爬行时经过面AD,
可将这个正方体展开,在展开图
上连接AC,与棱a(或b)交于D1(或
D2),蚂蚁沿AD1→D1C(或AD2→D2C)爬行,路线最短.类似地,蚂蚁经过面AB和AE爬行到顶点C,也分别有两条最短路线,因此,蚂蚁爬行的最短路线有6条.
课堂小结
两点的所有连线中,线段最短.即两点之间,线段最短.
连接两点间的线段的长度,叫做这两点的距离.
1.从课后习题中选取;
2.完成练习册本课时的习题。
课后作业
