【高效备课】人教版七(上) 4.3 角 4.3.1 角 课件
文档属性
| 名称 | 【高效备课】人教版七(上) 4.3 角 4.3.1 角 课件 |

|
|
| 格式 | pptx | ||
| 文件大小 | 1.2MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-09-12 00:00:00 | ||
图片预览






文档简介
(共23张PPT)
4.3 角
4.3.1 角
R·七年级上册
新课导入
角是一种基本的几何图形,生活中处处有“角”.
这节课我们将在已有的知识基础上,对角作进一步的研究.
学习目标
(1)明确角的意义及其表示方法.
(2)知道角的度量单位,会进行简单的单位换算.
(3)了解生产和生活中测量角的方法和相关工具,会用量角器量角的大小.
推进新课
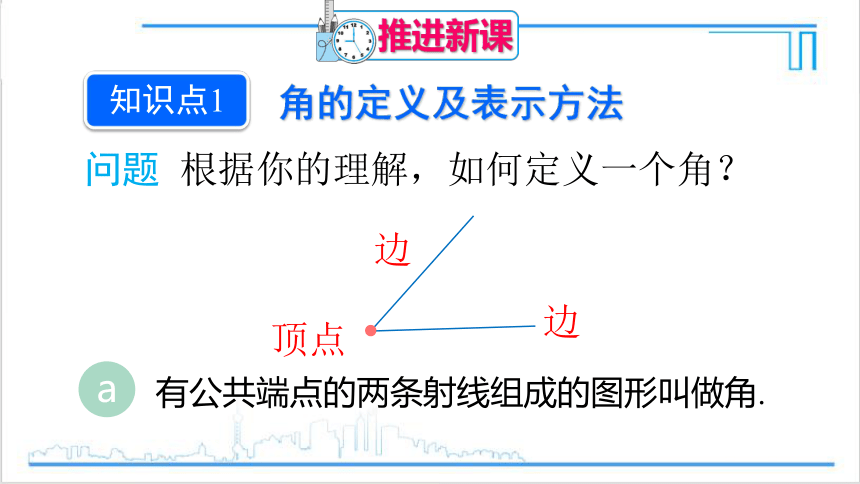
角的定义及表示方法
知识点1
问题 根据你的理解,如何定义一个角?
a
有公共端点的两条射线组成的图形叫做角.
顶点
边
边
b
角可以看作是由一条射线绕着它的端点旋转而形成的图形.
始边
终边
问题 你还能从其他角度给角下定义吗?
两条射线组成的图形叫做角.
角的大小由角的边的长短决定,边越长相应的角就越大.
判断下列说法的正误.
思考
平角是直线,周角是射线.
×
×
×
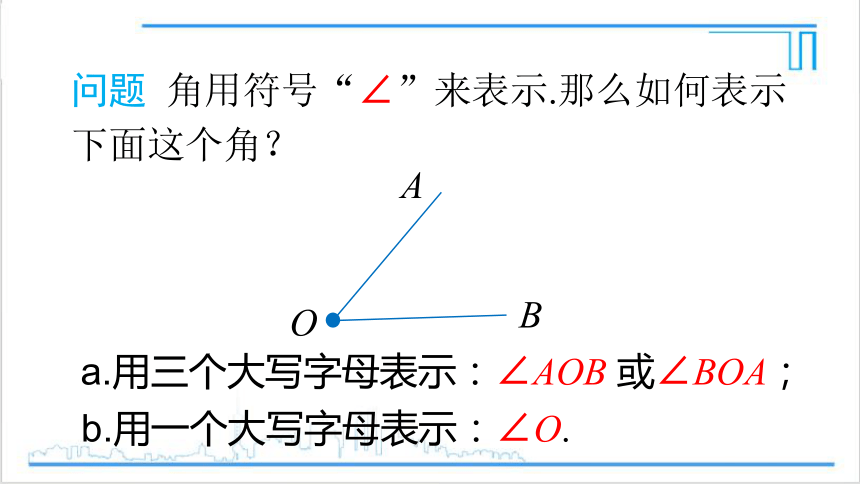
问题 角用符号“∠”来表示.那么如何表示下面这个角?
A
O
B
a.用三个大写字母表示:∠AOB 或∠BOA;
b.用一个大写字母表示:∠O.
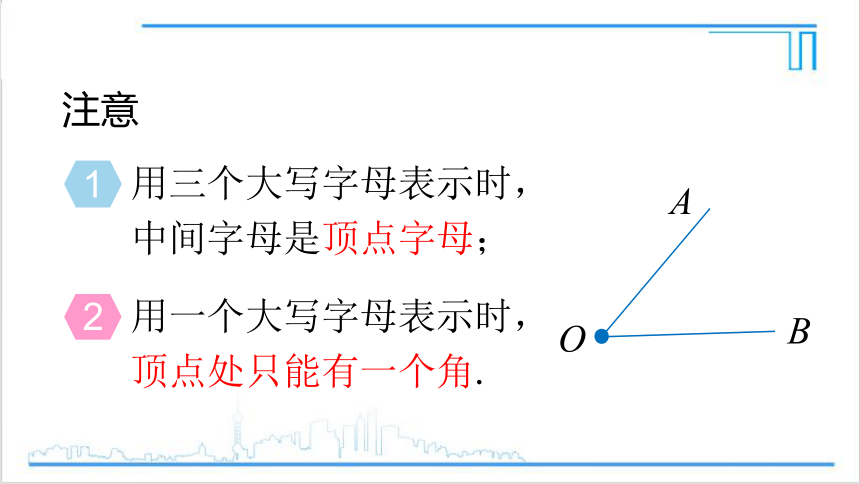
1
用三个大写字母表示时,中间字母是顶点字母;
用一个大写字母表示时,顶点处只能有一个角.
注意
2
A
O
B
思考 还有别的表示方法吗?
α
∠α
1
∠1
注意:这两种方法必须在图上标注后才能使用,并且只能表示单独的一个角.
a
用一个小写希腊字母加弧线表示;
b
用一个数字加弧线表示.
方法小结
强化练习
1.如图.
a.若用三个大写字母表示角,
则∠1可以表示为 ,
∠2可以表示为 .
b.∠BOC能写作∠O吗?为什么?
c.图中有多少个角?试分别表示出来.
∠AOB
∠COD
不能,因为以O为顶点的角不止一个.
∠1,∠2,∠BOC,∠AOC,∠BOD,∠AOD
角的度量
知识点2
问题 角的度量单位有哪些?它们又是如何定义的?
度、分、秒是常用的角的度量单位,它们之间是60进制的.
把一个周角360等分,每一份就是1度的角,记作1°;
定义
把1度的角60等分,每一份叫做1分的角,记作1′;
把1分的角60等分,每一份叫做1秒的角,记作1″.
问题 什么叫角度制?角的度量单位之间是如何换算的?
用度(°)、分(′)、秒(″)来测量角的大小的制度叫做角度制.角的度量单位使用60进制换算.1°=60′,1′ =60″.
问题 常用的角度度量工具是什么?使用时要注意什么?
最常用的度量角的工具是量角器.
注意:①对中(顶点对中心);②重合(一边与量角器的零刻度线重合);③读数(读出另一边所在线的度数).
强化练习
①时钟的时针一小时转过 度,分钟一分钟转过 度.
②6时整,钟表上的时针和分针构成多少度的角?8时呢?8时30分呢?
30
6
解:分别是180°,120°,75°的角.
【课本P134 练习 第1题】
随堂演练
1.能用∠1、∠AOB、∠O三种方法表示同一个角的图形是( )
A B C D
B
2.如图,下列说法正确的是( )
A.∠BAC 和∠DAE 不是同一个角
B.∠ABC 和∠ACB是同一个角
C.∠ADE 可以用∠D表示
D.∠ABC 可以用∠B表示
D
【课本P134 练习 第2题】
2.(1)35°等于多少分?等于多少秒?
(2) 3815‘和38.15°相等吗?如不相等,哪一个大?
【课本P134 练习 第3题】
3. 从蜂巢的入口处看,蜂巢由许多正六边形(六条边相等,六个角也相等)构成,按图示的方法,利用三角尺和圆规画出一个正六边形.
课堂小结
角
度量
定义
表示方法
有公共端点的两条射线组成的图形叫做角.
英文大写字母;希腊字母;数字
把一个周角360等分,每一份就是1度的角.
1.从课后习题中选取;
2.完成练习册本课时的习题。
课后作业
4.3 角
4.3.1 角
R·七年级上册
新课导入
角是一种基本的几何图形,生活中处处有“角”.
这节课我们将在已有的知识基础上,对角作进一步的研究.
学习目标
(1)明确角的意义及其表示方法.
(2)知道角的度量单位,会进行简单的单位换算.
(3)了解生产和生活中测量角的方法和相关工具,会用量角器量角的大小.
推进新课
角的定义及表示方法
知识点1
问题 根据你的理解,如何定义一个角?
a
有公共端点的两条射线组成的图形叫做角.
顶点
边
边
b
角可以看作是由一条射线绕着它的端点旋转而形成的图形.
始边
终边
问题 你还能从其他角度给角下定义吗?
两条射线组成的图形叫做角.
角的大小由角的边的长短决定,边越长相应的角就越大.
判断下列说法的正误.
思考
平角是直线,周角是射线.
×
×
×
问题 角用符号“∠”来表示.那么如何表示下面这个角?
A
O
B
a.用三个大写字母表示:∠AOB 或∠BOA;
b.用一个大写字母表示:∠O.
1
用三个大写字母表示时,中间字母是顶点字母;
用一个大写字母表示时,顶点处只能有一个角.
注意
2
A
O
B
思考 还有别的表示方法吗?
α
∠α
1
∠1
注意:这两种方法必须在图上标注后才能使用,并且只能表示单独的一个角.
a
用一个小写希腊字母加弧线表示;
b
用一个数字加弧线表示.
方法小结
强化练习
1.如图.
a.若用三个大写字母表示角,
则∠1可以表示为 ,
∠2可以表示为 .
b.∠BOC能写作∠O吗?为什么?
c.图中有多少个角?试分别表示出来.
∠AOB
∠COD
不能,因为以O为顶点的角不止一个.
∠1,∠2,∠BOC,∠AOC,∠BOD,∠AOD
角的度量
知识点2
问题 角的度量单位有哪些?它们又是如何定义的?
度、分、秒是常用的角的度量单位,它们之间是60进制的.
把一个周角360等分,每一份就是1度的角,记作1°;
定义
把1度的角60等分,每一份叫做1分的角,记作1′;
把1分的角60等分,每一份叫做1秒的角,记作1″.
问题 什么叫角度制?角的度量单位之间是如何换算的?
用度(°)、分(′)、秒(″)来测量角的大小的制度叫做角度制.角的度量单位使用60进制换算.1°=60′,1′ =60″.
问题 常用的角度度量工具是什么?使用时要注意什么?
最常用的度量角的工具是量角器.
注意:①对中(顶点对中心);②重合(一边与量角器的零刻度线重合);③读数(读出另一边所在线的度数).
强化练习
①时钟的时针一小时转过 度,分钟一分钟转过 度.
②6时整,钟表上的时针和分针构成多少度的角?8时呢?8时30分呢?
30
6
解:分别是180°,120°,75°的角.
【课本P134 练习 第1题】
随堂演练
1.能用∠1、∠AOB、∠O三种方法表示同一个角的图形是( )
A B C D
B
2.如图,下列说法正确的是( )
A.∠BAC 和∠DAE 不是同一个角
B.∠ABC 和∠ACB是同一个角
C.∠ADE 可以用∠D表示
D.∠ABC 可以用∠B表示
D
【课本P134 练习 第2题】
2.(1)35°等于多少分?等于多少秒?
(2) 3815‘和38.15°相等吗?如不相等,哪一个大?
【课本P134 练习 第3题】
3. 从蜂巢的入口处看,蜂巢由许多正六边形(六条边相等,六个角也相等)构成,按图示的方法,利用三角尺和圆规画出一个正六边形.
课堂小结
角
度量
定义
表示方法
有公共端点的两条射线组成的图形叫做角.
英文大写字母;希腊字母;数字
把一个周角360等分,每一份就是1度的角.
1.从课后习题中选取;
2.完成练习册本课时的习题。
课后作业
