【高效备课】人教版七(上) 第2章 整式的加减 章末复习 课件
文档属性
| 名称 | 【高效备课】人教版七(上) 第2章 整式的加减 章末复习 课件 |

|
|
| 格式 | pptx | ||
| 文件大小 | 296.9KB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-09-12 16:37:06 | ||
图片预览






文档简介
(共17张PPT)
章末复习
R·七年级上册
新课导入
导入课题
同学们,我们学完整式的加减这章后,你的印象如何?掌握得怎么样?还有哪些不够清楚?下面我们一起来进行本章的复习和小结.
学习目标
(1)加深本章学过的有关概念和运算法则的识记和理解.
(2)理清本章的知识结构,提升本章知识运用的方法技巧.
(3)进一步学会运用整式的加减表示实际问题中的数量关系.
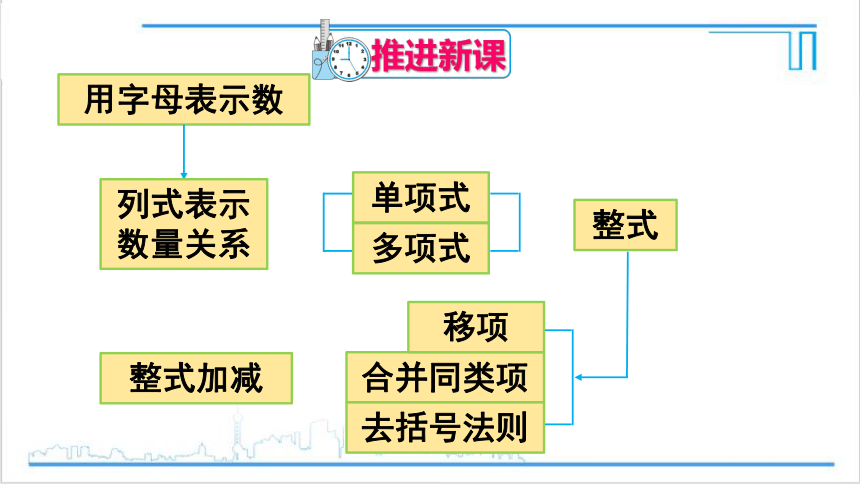
推进新课
用字母表示数
列式表示数量关系
单项式
多项式
整式
合并同类项
移项
去括号法则
整式加减
表示数或字母的积的式子叫做单项式,单项式中的数字因数叫做单项式系数,一个单项式中,所有字母的指数的和叫做单项式次数.
几个单项式的和叫做多项式,每个单项式叫做多项式的项,次数最高项的次数叫做多项式的次数,不含字母的项叫做常数项.
去括号的法则是如果括号外的因数是正数,去括号后原括号内各项的符号与原来的符号相同,如果括号外的因数是负数,去括号后原括号内各项的符号与原来的符号相反.
所含字母相同,而且相同字母的指数也相同的项叫做同类项,把多项式中的同类项合并成一项叫做合并同类项,合并同类项的法则是合并同类项后,所得项的系数是合并前各同类项的系数的和,且字母连同它的指数不变.
整式加减计算的一般步骤是如果有括号的先去括号,再合并同类项.
求整式的值的一般步骤是:先将式子化简,再代入数值进行计算.
例1 已知3(x+1)2+2|y-1| = 0,求多项式(x2+4xy-2y2)-(x2+y)-2(y2+xy)- (x-8y2)的值.
解:∵3(x+1)2 + 2|y-1| = 0
∴ 3(x+1)2 = 0
2|y-1| = 0
解得
原式= x2+4xy-2y2-x2-y-2y2-2xy- +4y2= -y+2xy- .
当x = -1,y = 1时,原式= -1+ 2×(-1)×1- =
x = -1
y = 1.
例2 计算
x2y - 3x2y
解:原式= - 2x2y
(6m2-4m-3)-2(m2-2m+1)
解:原式= 6m2-4m-3-2m2+4m-2
= 4m2 - 5
15+3(1-a)- (1-a-a2)+(1-a-a2-a3)
解:原式= 15+3-3a-1+a+a2+1-a-a2-a3
= -a3-3a+18
练习1 计算: (4x2-5xy)-( y2+2x2)+
2(3xy- y2- y2)
解:原式=4x2-5xy- y2-2x2+6xy- y2- y2
=2x2-y2+xy
练习2 先化简,再求值:2(x3-2y2)-(x-2y)-(x-3y2+2x3),其中x = -3,y = -2.
解:原式= 2x3-4y2-x+2y-x+3y2-2x3
= -y2-2x+2y
当x = -3,y = -2时,
原式 = -(-2)2 -2×(-3)+2×(-2)= -2.
例3 如图,是一组有规律的图案,第一个图案由4个基础图形组成,第2个图案由7个基础图形组成,……,第n(n是正整数)个图案是由__________个基础图形组成.
3n+1
随堂演练
基础巩固
1. 对于式子-7πx2yz,下列说法正确的是( )
A.它的系数为-7 B.它的次数为3
C.它的次数为5 D.它的系数为-7π
D
2. 多项式-3x2-6xy+1的各项分别为( )
A.-3x2,6xy,1 B.-3x2,-6xy,1
C.-3x2,-6xy,-1 D.3x2,6xy,1
B
3. 先化简,再求值.
5x2+4-3x2-5x-2x2-5+6x,其中x = -3
解:原式 = (5-3-2)x2+(-5+6)x-1
= x-1.
当x = -3时,原式 = -3 -1 = -4.
综合应用
4. 一种商品每件成本为a元,原来按成本增加22%定出价格,每件售价多少元?现在由于库存积压减价,按原价的85%出售,现售价多少元?每件还能盈利多少元?
解:售价为a×(1+22%)= 1.22a(元)
现售价为1.22a×85% = 1.037a(元)
每件还能盈利:1.037a - a = 0.037a(元)
拓展延伸
5. 有理数a,b,c在数轴上的位置如图所示,化简
解:由题意b原式= -(b-a)-(a+b)+c+(b-c)+(a+c)
= -b+a-a-b+c+b-c+a+c
= a+c-b
课后作业
1.从课后习题中选取;
2.完成练习册本课时的习题。
章末复习
R·七年级上册
新课导入
导入课题
同学们,我们学完整式的加减这章后,你的印象如何?掌握得怎么样?还有哪些不够清楚?下面我们一起来进行本章的复习和小结.
学习目标
(1)加深本章学过的有关概念和运算法则的识记和理解.
(2)理清本章的知识结构,提升本章知识运用的方法技巧.
(3)进一步学会运用整式的加减表示实际问题中的数量关系.
推进新课
用字母表示数
列式表示数量关系
单项式
多项式
整式
合并同类项
移项
去括号法则
整式加减
表示数或字母的积的式子叫做单项式,单项式中的数字因数叫做单项式系数,一个单项式中,所有字母的指数的和叫做单项式次数.
几个单项式的和叫做多项式,每个单项式叫做多项式的项,次数最高项的次数叫做多项式的次数,不含字母的项叫做常数项.
去括号的法则是如果括号外的因数是正数,去括号后原括号内各项的符号与原来的符号相同,如果括号外的因数是负数,去括号后原括号内各项的符号与原来的符号相反.
所含字母相同,而且相同字母的指数也相同的项叫做同类项,把多项式中的同类项合并成一项叫做合并同类项,合并同类项的法则是合并同类项后,所得项的系数是合并前各同类项的系数的和,且字母连同它的指数不变.
整式加减计算的一般步骤是如果有括号的先去括号,再合并同类项.
求整式的值的一般步骤是:先将式子化简,再代入数值进行计算.
例1 已知3(x+1)2+2|y-1| = 0,求多项式(x2+4xy-2y2)-(x2+y)-2(y2+xy)- (x-8y2)的值.
解:∵3(x+1)2 + 2|y-1| = 0
∴ 3(x+1)2 = 0
2|y-1| = 0
解得
原式= x2+4xy-2y2-x2-y-2y2-2xy- +4y2= -y+2xy- .
当x = -1,y = 1时,原式= -1+ 2×(-1)×1- =
x = -1
y = 1.
例2 计算
x2y - 3x2y
解:原式= - 2x2y
(6m2-4m-3)-2(m2-2m+1)
解:原式= 6m2-4m-3-2m2+4m-2
= 4m2 - 5
15+3(1-a)- (1-a-a2)+(1-a-a2-a3)
解:原式= 15+3-3a-1+a+a2+1-a-a2-a3
= -a3-3a+18
练习1 计算: (4x2-5xy)-( y2+2x2)+
2(3xy- y2- y2)
解:原式=4x2-5xy- y2-2x2+6xy- y2- y2
=2x2-y2+xy
练习2 先化简,再求值:2(x3-2y2)-(x-2y)-(x-3y2+2x3),其中x = -3,y = -2.
解:原式= 2x3-4y2-x+2y-x+3y2-2x3
= -y2-2x+2y
当x = -3,y = -2时,
原式 = -(-2)2 -2×(-3)+2×(-2)= -2.
例3 如图,是一组有规律的图案,第一个图案由4个基础图形组成,第2个图案由7个基础图形组成,……,第n(n是正整数)个图案是由__________个基础图形组成.
3n+1
随堂演练
基础巩固
1. 对于式子-7πx2yz,下列说法正确的是( )
A.它的系数为-7 B.它的次数为3
C.它的次数为5 D.它的系数为-7π
D
2. 多项式-3x2-6xy+1的各项分别为( )
A.-3x2,6xy,1 B.-3x2,-6xy,1
C.-3x2,-6xy,-1 D.3x2,6xy,1
B
3. 先化简,再求值.
5x2+4-3x2-5x-2x2-5+6x,其中x = -3
解:原式 = (5-3-2)x2+(-5+6)x-1
= x-1.
当x = -3时,原式 = -3 -1 = -4.
综合应用
4. 一种商品每件成本为a元,原来按成本增加22%定出价格,每件售价多少元?现在由于库存积压减价,按原价的85%出售,现售价多少元?每件还能盈利多少元?
解:售价为a×(1+22%)= 1.22a(元)
现售价为1.22a×85% = 1.037a(元)
每件还能盈利:1.037a - a = 0.037a(元)
拓展延伸
5. 有理数a,b,c在数轴上的位置如图所示,化简
解:由题意b
= -b+a-a-b+c+b-c+a+c
= a+c-b
课后作业
1.从课后习题中选取;
2.完成练习册本课时的习题。
