【高效备课】人教版七(上) 1.2 有理数 1.2.4 绝对值 第2课时 有理数的大小比较 课件
文档属性
| 名称 | 【高效备课】人教版七(上) 1.2 有理数 1.2.4 绝对值 第2课时 有理数的大小比较 课件 |

|
|
| 格式 | pptx | ||
| 文件大小 | 396.6KB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-09-12 00:00:00 | ||
图片预览







文档简介
(共23张PPT)
1.2.4 绝对值
第2课时 有理数的大小比较
R·七年级上册
新课导入
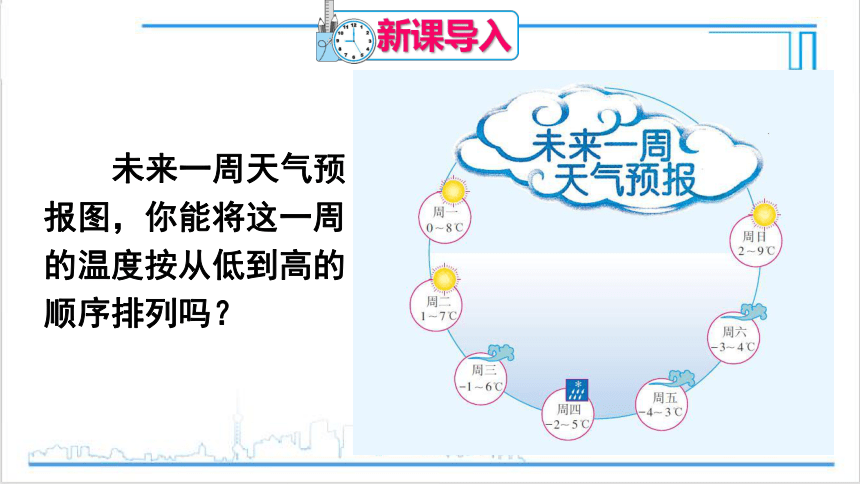
未来一周天气预报图,你能将这一周的温度按从低到高的顺序排列吗?
学习目标:
1.进一步理解绝对值的意义.
2.会进行有理数的大小比较.
推进新课
有理数的大小比较
知识点1
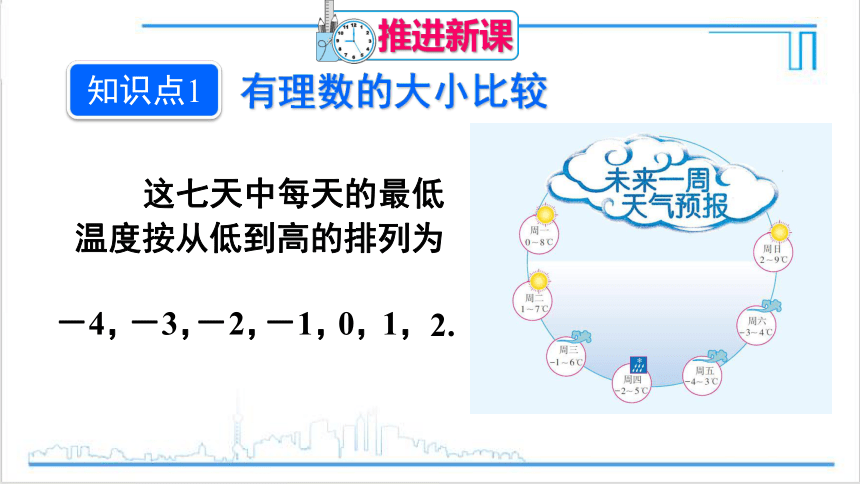
这七天中每天的最低温度按从低到高的排列为
-4,
-3,
-2,
-1,
0,
1,
2.
我们已知两个正数(或0)之间怎样比较大小,例如
0 < 1,1 < 2,2 < 3,…
任意两个有理数(例如-4和-3, -2和0,-1和1)怎样比较大小呢?
-4,
-3,
-2,
-1,
0,
1,
按照这个顺序排列的温度,在温度计上所对应的点是从下到上的;按照这个顺序把这些数表示在数轴上,表示它们的各点的顺序应该是从左到右的.
-1
0
1
2
-2
-3
-4
-1
0
1
2
-2
-3
-4
数学中规定:在数轴上表示有理数,它们从左到右的顺序,就是从小到大的顺序,即左边的数小于右边的数.
-6 < -5,-5 < -4,-4 < -3,-2 < 0,-1 < 1
一般地,
(1)正数大于0,0大于负数,正数大于负数;
(2)两个负数,绝对值大的反而小.
对于正数、0和负数这三类数,它们之间有什么大小关系?
思考
例如,1 ____ 0,0 ____-1,1 ____ -1,
-1____ -2
>
>
>
>
同号两数、异号两数大小比较
知识点2
例 比较下列各对数的大小:
(1) -(-1)和-(+2)
(2)
(3)-(-0.3)和
解:(1)先化简, -(-1)=1,-(+2)=-2.
因为正数大于负数,所以1>-2,即
-(-1)> -(+2).
(2)这是两个负数比较大小,先求它们的绝对值.
因为
即
所以
(3)先化简,-(-0.3)=0.3,
因为
所以
①比较两数大小时,如果有括号和绝对值时,怎么办?
先将括号和绝对值化简,再比较大小.
②异号两数大小怎样比较?同号两数大小怎样比较?
若两数异号,则正数大于负数;若两数同号,先考虑它们的绝对值.
思考
说说你对绝对值的认识?有理数怎样比较大小?
归纳:
(1)一个正数的绝对值是它本身;一个负数的绝对值是它的相反数;0的绝对值是0.
(2)若a为有理数,则| a | ≥ 0.
(3)零作为一个特殊的数,有它特殊的属性:
绝对值最小的数、相反数是它本身、绝对值是它本身.
(4)有理数比较大小的方法:
方法1.数轴上表示的两个数,右边的总比左边的大;
方法2.正数大于0,0大于负数,正数大于负数;两个负数,绝对值大的反而小 .
随堂演练
1. 下面四个不等式中,正确的是( )
A. |-2|>|-3| B. | 2 |>| 3 |
C. 2>|-3| D. |-2|<|-3|
D
基础巩固
2. 比较下列各数的大小:
(1)3和-5; (2)-3和-5;
(3)-2.5和-|-2.5|; (4)- 和- .
【课本P13 练习 】
2. 比较下列各数的大小:
(1)3和-5; (2)-3和-5;
(3)-2.5和-|-2.5|; (4)- 和- .
【课本P13 练习 】
2. 比较下列各数的大小:
(1)3和-5; (2)-3和-5;
(3)-2.5和-|-2.5|; (4)- 和- .
【课本P13 练习 】
2. (1)-1与0之间还有负数吗? 与0之间呢?如有,请举例.
(2)-3与-1之间有负整数吗?-2与2之间有哪些整数?
(3)有比-1大的负整数吗?
(4)写出3个小于-100并且大于-103的数.
有,
有,
有,
-2
-1,0,1
没有
-101,-101.5,-102
综合应用
3.已知a、b为有理数,且a<0,b>0,|a|>|b|,则( )
A.a <-b < b <-a B.-b < a < b <-a
C.-a < b <-b < a D.-b < b <-a < a
拓展延伸
A
课堂小结
-1
0
1
2
-2
-3
-4
一般地,
(1)正数大于0,0大于负数,正数大于负数;
(2)两个负数,绝对值大的反而小.
1.从课后习题中选取;
2.完成练习册本课时的习题。
课后作业
1.2.4 绝对值
第2课时 有理数的大小比较
R·七年级上册
新课导入
未来一周天气预报图,你能将这一周的温度按从低到高的顺序排列吗?
学习目标:
1.进一步理解绝对值的意义.
2.会进行有理数的大小比较.
推进新课
有理数的大小比较
知识点1
这七天中每天的最低温度按从低到高的排列为
-4,
-3,
-2,
-1,
0,
1,
2.
我们已知两个正数(或0)之间怎样比较大小,例如
0 < 1,1 < 2,2 < 3,…
任意两个有理数(例如-4和-3, -2和0,-1和1)怎样比较大小呢?
-4,
-3,
-2,
-1,
0,
1,
按照这个顺序排列的温度,在温度计上所对应的点是从下到上的;按照这个顺序把这些数表示在数轴上,表示它们的各点的顺序应该是从左到右的.
-1
0
1
2
-2
-3
-4
-1
0
1
2
-2
-3
-4
数学中规定:在数轴上表示有理数,它们从左到右的顺序,就是从小到大的顺序,即左边的数小于右边的数.
-6 < -5,-5 < -4,-4 < -3,-2 < 0,-1 < 1
一般地,
(1)正数大于0,0大于负数,正数大于负数;
(2)两个负数,绝对值大的反而小.
对于正数、0和负数这三类数,它们之间有什么大小关系?
思考
例如,1 ____ 0,0 ____-1,1 ____ -1,
-1____ -2
>
>
>
>
同号两数、异号两数大小比较
知识点2
例 比较下列各对数的大小:
(1) -(-1)和-(+2)
(2)
(3)-(-0.3)和
解:(1)先化简, -(-1)=1,-(+2)=-2.
因为正数大于负数,所以1>-2,即
-(-1)> -(+2).
(2)这是两个负数比较大小,先求它们的绝对值.
因为
即
所以
(3)先化简,-(-0.3)=0.3,
因为
所以
①比较两数大小时,如果有括号和绝对值时,怎么办?
先将括号和绝对值化简,再比较大小.
②异号两数大小怎样比较?同号两数大小怎样比较?
若两数异号,则正数大于负数;若两数同号,先考虑它们的绝对值.
思考
说说你对绝对值的认识?有理数怎样比较大小?
归纳:
(1)一个正数的绝对值是它本身;一个负数的绝对值是它的相反数;0的绝对值是0.
(2)若a为有理数,则| a | ≥ 0.
(3)零作为一个特殊的数,有它特殊的属性:
绝对值最小的数、相反数是它本身、绝对值是它本身.
(4)有理数比较大小的方法:
方法1.数轴上表示的两个数,右边的总比左边的大;
方法2.正数大于0,0大于负数,正数大于负数;两个负数,绝对值大的反而小 .
随堂演练
1. 下面四个不等式中,正确的是( )
A. |-2|>|-3| B. | 2 |>| 3 |
C. 2>|-3| D. |-2|<|-3|
D
基础巩固
2. 比较下列各数的大小:
(1)3和-5; (2)-3和-5;
(3)-2.5和-|-2.5|; (4)- 和- .
【课本P13 练习 】
2. 比较下列各数的大小:
(1)3和-5; (2)-3和-5;
(3)-2.5和-|-2.5|; (4)- 和- .
【课本P13 练习 】
2. 比较下列各数的大小:
(1)3和-5; (2)-3和-5;
(3)-2.5和-|-2.5|; (4)- 和- .
【课本P13 练习 】
2. (1)-1与0之间还有负数吗? 与0之间呢?如有,请举例.
(2)-3与-1之间有负整数吗?-2与2之间有哪些整数?
(3)有比-1大的负整数吗?
(4)写出3个小于-100并且大于-103的数.
有,
有,
有,
-2
-1,0,1
没有
-101,-101.5,-102
综合应用
3.已知a、b为有理数,且a<0,b>0,|a|>|b|,则( )
A.a <-b < b <-a B.-b < a < b <-a
C.-a < b <-b < a D.-b < b <-a < a
拓展延伸
A
课堂小结
-1
0
1
2
-2
-3
-4
一般地,
(1)正数大于0,0大于负数,正数大于负数;
(2)两个负数,绝对值大的反而小.
1.从课后习题中选取;
2.完成练习册本课时的习题。
课后作业
