多项式的乘法
图片预览





文档简介
课件19张PPT。回顾与思考② 再把所得的积相加。① 将单项式分别乘以多项式的各项,① 不能漏乘:即单项式要乘遍多项式的每一项② 去括号时注意符号的确定.(a+b)X= ?
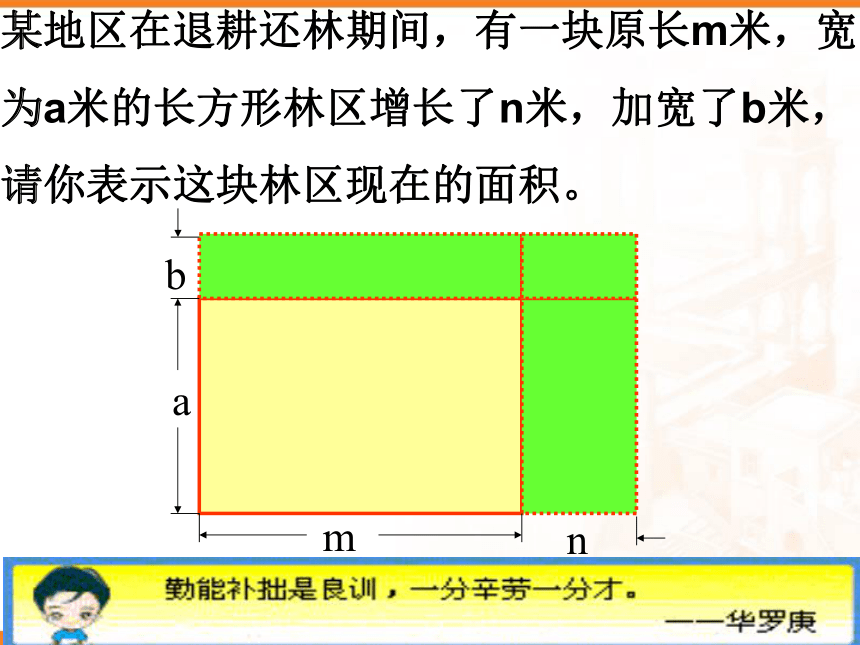
(a+b)X=aX+bX(a+b)X=(a+b)(m+n)讨论 探究:当X=m+n时, (a+b)X=?某地区在退耕还林期间,有一块原长m米,宽
为a米的长方形林区增长了n米,加宽了b米,
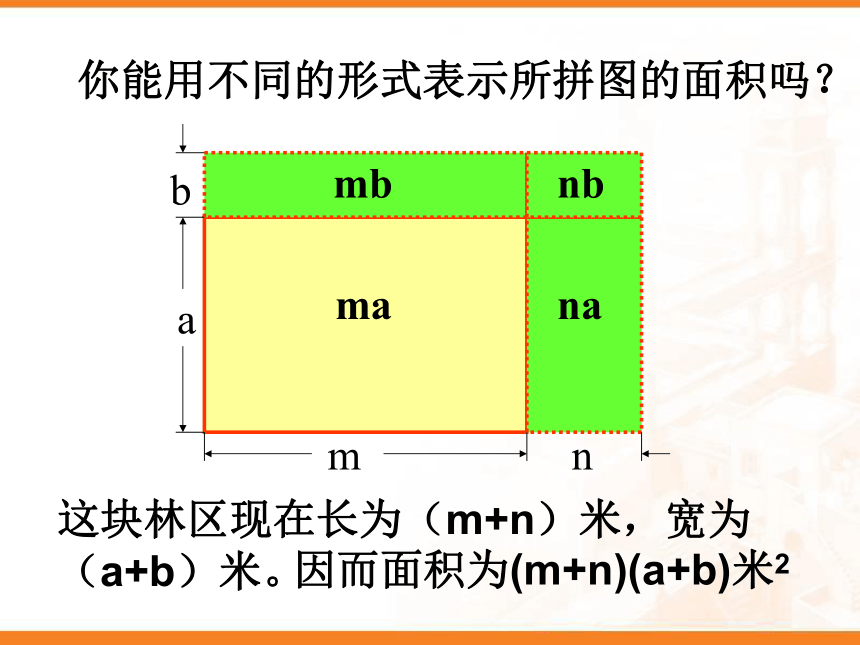
请你表示这块林区现在的面积。manambnb你能用不同的形式表示所拼图的面积吗?这块林区现在长为(m+n)米,宽为(a+b)米。因而面积为(m+n)(a+b)米2
由于(m+n)(a+b)和(ma+mb+na+nb)表示同一块地的面积,故有:
(m+n)(a+b)=ma+ mb+ na+ nb如何进行多项式与多项式相乘的 运算 ?实际上,把(m+n)看成一个整体,有:= ma+mb+na+nb(m+n)(a+b)= (m+n)a+(m+n)b 15.2.4多项式与多项式相乘(a+b)(m+n)=am1234+an+bm+bn多项式的乘法法则例题解析 【例1】计算: (1)(x+2)(x?3), (2)(3x -1)(2x+1)。?3x+2x=x2 -x-6 -2×3(2) (3x -1)(2x+1)=3x?2x+3x? 1-1?2 x?1=6x2+3x-2 x?1=6x2 +x?1. 你注意到了吗? 多项式乘以多项式,展开后项数很有规律,在合并同类项之前,展开式的项数恰好等于两个多项式的项数的积。 【例2】计算: (1)(x?3y)(x+7y)
(2)(2x + 5y)(3x?2y+2Z)。 注意:
1、必须做到不重复,不遗漏.2、注意确定积中每一项的符号.
3、结果应化为最简式
{合并同类项}. 练习、计算:(1) (2a–3b)(a+5b) ;(2) (xy–z)(2xy+z) ;(3) (x–1)(x2+x+1) ;(4) (a+b)2;(5) (3a–2)(a–1)–(a+1)(a+2) ;(6) (x+y)(2x–y)(3x+2y).注 意 !1.计算(a+b)2应该这样做:
(a+b)2=(a+b)(a+b)
=a2+ab+ab+b2
=a2+2ab+b2
切记 一般情况下
(a+b)2不等a2+b2 .注 意 !2.(3a–2)(a–1)–(a+1)(a+2)是多项式的积与积的差,后两个多项式乘积的展开式要用括号括起来。
3. (x+y)(2x–y)(3x+2y)是三个多项式相乘,应该选其中的两个先相乘,把它们的积用括号括起来,再与第三个相乘。
方法与规律延伸训练:填空:观察上面四个等式,你能发现什么规律?你能根据这个规律解决下面的问题吗? 【例3】解方程与不等式: (1).(x-3)(x-2)+18=(x+9)(x+1)
(2)(3x+4)(3x-4)<9(x-2)(x+3) 挑战极限: 如果(x2+bx+8)(x2 – 3x+c)的乘积中不含x2和x3的项,求b、c的值。解:原式= x4 – 3x3 + c x2 +bx3
– 3bx2 +bcx+8 x2– 24x+8cX2项系数为:c –3b+8X3项系数为:b – 3= 0= 0∴ b=3 , c=1转化思想多项式与多项式相乘的法则生活中处处有数学思想方法收获应用收获知识收获谈收获谢谢再见别忘了完成作业哦!
(a+b)X=aX+bX(a+b)X=(a+b)(m+n)讨论 探究:当X=m+n时, (a+b)X=?某地区在退耕还林期间,有一块原长m米,宽
为a米的长方形林区增长了n米,加宽了b米,
请你表示这块林区现在的面积。manambnb你能用不同的形式表示所拼图的面积吗?这块林区现在长为(m+n)米,宽为(a+b)米。因而面积为(m+n)(a+b)米2
由于(m+n)(a+b)和(ma+mb+na+nb)表示同一块地的面积,故有:
(m+n)(a+b)=ma+ mb+ na+ nb如何进行多项式与多项式相乘的 运算 ?实际上,把(m+n)看成一个整体,有:= ma+mb+na+nb(m+n)(a+b)= (m+n)a+(m+n)b 15.2.4多项式与多项式相乘(a+b)(m+n)=am1234+an+bm+bn多项式的乘法法则例题解析 【例1】计算: (1)(x+2)(x?3), (2)(3x -1)(2x+1)。?3x+2x=x2 -x-6 -2×3(2) (3x -1)(2x+1)=3x?2x+3x? 1-1?2 x?1=6x2+3x-2 x?1=6x2 +x?1. 你注意到了吗? 多项式乘以多项式,展开后项数很有规律,在合并同类项之前,展开式的项数恰好等于两个多项式的项数的积。 【例2】计算: (1)(x?3y)(x+7y)
(2)(2x + 5y)(3x?2y+2Z)。 注意:
1、必须做到不重复,不遗漏.2、注意确定积中每一项的符号.
3、结果应化为最简式
{合并同类项}. 练习、计算:(1) (2a–3b)(a+5b) ;(2) (xy–z)(2xy+z) ;(3) (x–1)(x2+x+1) ;(4) (a+b)2;(5) (3a–2)(a–1)–(a+1)(a+2) ;(6) (x+y)(2x–y)(3x+2y).注 意 !1.计算(a+b)2应该这样做:
(a+b)2=(a+b)(a+b)
=a2+ab+ab+b2
=a2+2ab+b2
切记 一般情况下
(a+b)2不等a2+b2 .注 意 !2.(3a–2)(a–1)–(a+1)(a+2)是多项式的积与积的差,后两个多项式乘积的展开式要用括号括起来。
3. (x+y)(2x–y)(3x+2y)是三个多项式相乘,应该选其中的两个先相乘,把它们的积用括号括起来,再与第三个相乘。
方法与规律延伸训练:填空:观察上面四个等式,你能发现什么规律?你能根据这个规律解决下面的问题吗? 【例3】解方程与不等式: (1).(x-3)(x-2)+18=(x+9)(x+1)
(2)(3x+4)(3x-4)<9(x-2)(x+3) 挑战极限: 如果(x2+bx+8)(x2 – 3x+c)的乘积中不含x2和x3的项,求b、c的值。解:原式= x4 – 3x3 + c x2 +bx3
– 3bx2 +bcx+8 x2– 24x+8cX2项系数为:c –3b+8X3项系数为:b – 3= 0= 0∴ b=3 , c=1转化思想多项式与多项式相乘的法则生活中处处有数学思想方法收获应用收获知识收获谈收获谢谢再见别忘了完成作业哦!
