第一章 空间向量与立体几何(章末总结) 课件(共28张PPT)
文档属性
| 名称 | 第一章 空间向量与立体几何(章末总结) 课件(共28张PPT) |

|
|
| 格式 | pptx | ||
| 文件大小 | 53.2MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教A版(2019) | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-09-12 00:00:00 | ||
图片预览







文档简介
(共28张PPT)
章末总结
第 一 章空间向量与立体几何
人教A版2019选修第一册
01知识结构
PART ONE
思维导图
知识结构
加法、减法、数乘运算
减法:三角形法则
加法:三角形法则或平行四边形法则
数乘:ka,k为正数,负数,零
运算律
加法交换律
数乘分配律
加法结合律
线性运算
知识结构
空间中的两个非零向量,,定义||||cos θ为,的数量积·.
空间向量的数量积
数量积
数量积的性质
①⊥ ·=0;
②·=||||cos〈,〉=||2=2;
③ 零向量与任意向量的数量积为0,即·=0;
④ |·|≤||·||.
⑤cos〈,〉=
证明两个向量垂直
求模长
夹角公式
知识结构
四点共面
知识结构
设u1,u2分别是直线l1,l2的方向向量,n1,n2分别是平面α,β的法向量.
线线平行 l1∥l2 _________ ____________________
线面平行 l1∥α ______________ ________________
面面平行 α∥β ______________ ________________
线线垂直 l1⊥l2 _____________ ________________
线面垂直 l1⊥α ______________ ________________
面面垂直 α⊥β ______________ _____________
平行、垂直
知识结构
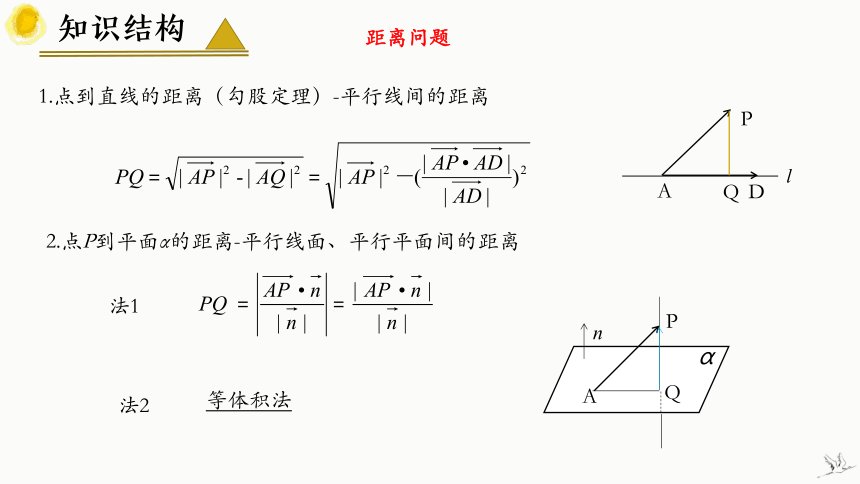
1.点到直线的距离(勾股定理)-平行线间的距离
2.点P到平面α的距离-平行线面、平行平面间的距离
距离问题
P
A
Q
D
A
Q
P
法1
法2
等体积法
知识结构
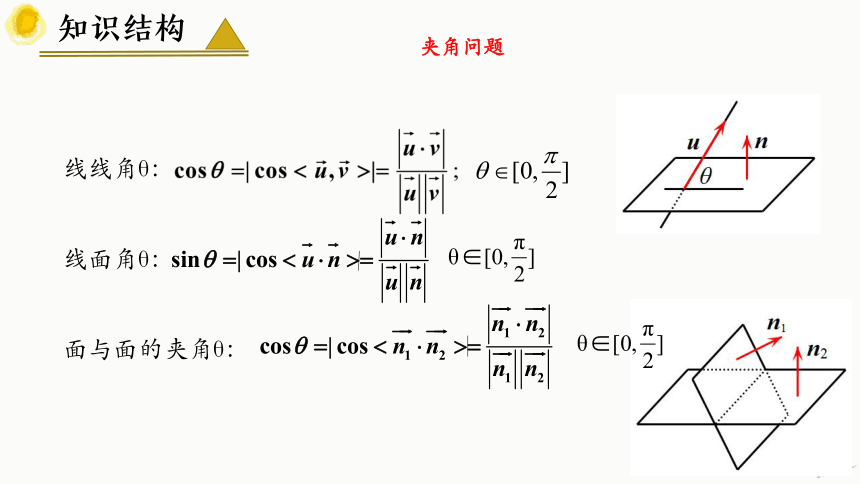
夹角问题
线线角θ:
线面角θ:
面与面的夹角θ:
02用空间向量研究问题
PART ONE
知识应用
1.已知空间向量 ,则 =__________;
向量 与的夹角为___________.
解析 由 ,则=(3,0,3),所以
=,
==,所以向量与的夹角为 .
1.空间向量的运算
ABC
知识应用
1.空间向量的运算
知识应用
2. 空间向量解决线面位置关系问题
1.如图,由直三棱柱ABC-A1B1C1和四棱锥D-BB1C1C构成的几何体中,∠BAC=,AB=1,BC=BB1=2,
C1D=CD=平面CC1D 平面ACC1A1
(1)求证:AC DC1;
(2)若M为 DC1中点,求证:AM//平面DBB1;
解:(1) 在直三棱柱ABC-A1B1C1中,
CC1 平面ABC,又AC 平面ABC,∴CC1 AC ,
∵平面CC1D 平面ACC1A1,且平面 CC1D 平面ACC1A1=CC1,
又AC 平面 ACC1A1,∴AC 平面CC1D,
又 DC1 平面CC1D,∴AC DC1
知识应用
(2)直三棱柱ABC-A1B1C1中,∵AA1平面A1B1C1,而A1B1,A1C1 平面A1B1C1,∴AA1,AA1又∠BAC=,
建立如图所示的空间直角坐标系,则A(2,0,0),C(2,,0),C1(0,,0),B(2,0,1),B1(0,0,1),D(1,,2)
所以,,-1)
设平面DBB1 的一个法向量为,则,
即,令y=1,则(0,1,,
∵M为DC1的中点,则M(),所以,
因为,所以,又 AM平面DBB1,∴AM//平面DBB1.
知识应用
2. 如图所示,已知平面,四边形为矩形,,,分别为,的中点.求证:
(1) //平面;
(2) 平面平面.
设,则,,,
,,因为分别为的中点,
所以.
解: 如图所示,以为坐标原点,,,所在的直线分别为,,轴,建立空间直角坐标系.
知识应用
所以,,,
所以.
又因为平面,所以平面.
(2) 由(1)可知,,.
设平面的法向量为,
则即
知识应用
令,得,,
则.
设平面的法向量为,
则即
令,得,,则.
所以, 所以平面平面.
知识应用
1.某校积极开展社团活动,在一次社团活动过程中,一个数学兴趣小组发现《九章算术》中提到了“刍甍”这个五面体,于是他们仿照该模型设计了一道数学探究题,如图1,E、F、G分别是正方形的三边AB、CD、AD的中点,先沿着虚线段FG将等腰直角三角形FDG裁掉,再将剩下的五边形ABCFG沿着线段EF折起,连接AB、CG就得到了一个“刍甍”(如图2).
(1)若O是四边形EBCF对角线的交点,
求证:AO//平面GCF;
(2)若二面角A-EF-B是直二面角,求点B到平面GCF的距离.
3.空间向量解决距离问题
知识应用
(1)证明:取线段CF中点H,连接OH、GH,由图1可知,四边形EBCF是矩形,且CB=2EB,
∴O是线段BF与CE的中点,∴ OH//BC且OH=,在图1中知AG//BC且AG=BC,EF//BC且EF=BC,
所以在图2中,AG//BC且AG=BC,AG//OH且AG=OH,∴四边形AOHG是平行四边形,则AO//HG,
由于AO 平面GCF,HG平面GCF,∴AO//平面GCF.
知识应用
(2)解:由图1,EF,EF折起后在图2中仍有 EF,EF,
∴即为二面角A-EF-E 的平面角,∴=,
以E为坐标原点,分别为 轴和 轴正向建立空间直角坐标系E-xyz,
则B(2,0,0)、C(4,2,0)、F(0,4,0)、A(0,0,2)、G(0,2,2),
∴,
设平面GCF 的一个法向量为
由,得,取,则z=1,
于是平面GCF的一个法向量 =(0,1,1)
点B到平面GCF的距离为d==.
知识应用
4.空间向量解决夹角问题
1.如图,四边形ABCD为菱形,∠ABC=120°,E,F是平面ABCD同一侧的两点,BE⊥平面ABCD,DF⊥平面ABCD,BE=2DF,AE⊥EC.
(1)证明:平面AEC⊥平面AFC;
(2)求直线AE与直线CF所成角的余弦值.
知识应用
知识应用
知识应用
2.如图,在正三棱柱ABC-A1B1C1中,2AB=AA1=4,CE=EC1,AF=3FA1.
(1)证明:BE 平面B1EF;
(2)求面EBF与面BFA夹角的余弦值.
解:(1)由条件可知BE=,BF=,EF=,
满足 ,EF BE.
BE=B1E=,BB1=4,
满足,BE B1E.
又 B1E, BE平面B1EF.
知识应用
(2)以AC 的中点O为坐标原点,建立如图所示的空间直角坐标系 O- xyz,
则B(0,,E(-1,0,2),F (1,0,3). ,,
设平面 BEF 的法向量为,,
取 得 = (.
易得平面 ABF 的一个法向量为 ,
cos,
面EBF与面BFA夹角的余弦值.
例3 如图,已知三棱柱ABC-A1B1C1的侧棱与底面垂直,AA1=AB=AC=1,AB⊥AC,M,N分别是CC1,BC的中点,点P在直线A1B1上,且A1P=λA1B1.
(1)证明:无论λ取何值,总有AM⊥PN;
(2)是否存在点P,使得平面PMN与平面ABC所成的角为30°?若存在,试确定点P的位置;若不存在,请说明理由.
知识应用
5.空间向量探索性问题
1.如图,已知三棱柱ABC-A1B1C1的侧棱与底面垂直,AA1=AB=AC=1,AB⊥AC,M,N分别是CC1,BC的中点,点P在直线A1B1上,且A1P=λA1B1.
(1)证明:无论λ取何值,总有AM⊥PN;
(2)是否存在点P,使得平面PMN与平面ABC所成的角为30°?若存在,试确定点P的位置;若不存在,请说明理由.
知识应用
知识应用
章末总结
第 一 章空间向量与立体几何
人教A版2019选修第一册
01知识结构
PART ONE
思维导图
知识结构
加法、减法、数乘运算
减法:三角形法则
加法:三角形法则或平行四边形法则
数乘:ka,k为正数,负数,零
运算律
加法交换律
数乘分配律
加法结合律
线性运算
知识结构
空间中的两个非零向量,,定义||||cos θ为,的数量积·.
空间向量的数量积
数量积
数量积的性质
①⊥ ·=0;
②·=||||cos〈,〉=||2=2;
③ 零向量与任意向量的数量积为0,即·=0;
④ |·|≤||·||.
⑤cos〈,〉=
证明两个向量垂直
求模长
夹角公式
知识结构
四点共面
知识结构
设u1,u2分别是直线l1,l2的方向向量,n1,n2分别是平面α,β的法向量.
线线平行 l1∥l2 _________ ____________________
线面平行 l1∥α ______________ ________________
面面平行 α∥β ______________ ________________
线线垂直 l1⊥l2 _____________ ________________
线面垂直 l1⊥α ______________ ________________
面面垂直 α⊥β ______________ _____________
平行、垂直
知识结构
1.点到直线的距离(勾股定理)-平行线间的距离
2.点P到平面α的距离-平行线面、平行平面间的距离
距离问题
P
A
Q
D
A
Q
P
法1
法2
等体积法
知识结构
夹角问题
线线角θ:
线面角θ:
面与面的夹角θ:
02用空间向量研究问题
PART ONE
知识应用
1.已知空间向量 ,则 =__________;
向量 与的夹角为___________.
解析 由 ,则=(3,0,3),所以
=,
==,所以向量与的夹角为 .
1.空间向量的运算
ABC
知识应用
1.空间向量的运算
知识应用
2. 空间向量解决线面位置关系问题
1.如图,由直三棱柱ABC-A1B1C1和四棱锥D-BB1C1C构成的几何体中,∠BAC=,AB=1,BC=BB1=2,
C1D=CD=平面CC1D 平面ACC1A1
(1)求证:AC DC1;
(2)若M为 DC1中点,求证:AM//平面DBB1;
解:(1) 在直三棱柱ABC-A1B1C1中,
CC1 平面ABC,又AC 平面ABC,∴CC1 AC ,
∵平面CC1D 平面ACC1A1,且平面 CC1D 平面ACC1A1=CC1,
又AC 平面 ACC1A1,∴AC 平面CC1D,
又 DC1 平面CC1D,∴AC DC1
知识应用
(2)直三棱柱ABC-A1B1C1中,∵AA1平面A1B1C1,而A1B1,A1C1 平面A1B1C1,∴AA1,AA1又∠BAC=,
建立如图所示的空间直角坐标系,则A(2,0,0),C(2,,0),C1(0,,0),B(2,0,1),B1(0,0,1),D(1,,2)
所以,,-1)
设平面DBB1 的一个法向量为,则,
即,令y=1,则(0,1,,
∵M为DC1的中点,则M(),所以,
因为,所以,又 AM平面DBB1,∴AM//平面DBB1.
知识应用
2. 如图所示,已知平面,四边形为矩形,,,分别为,的中点.求证:
(1) //平面;
(2) 平面平面.
设,则,,,
,,因为分别为的中点,
所以.
解: 如图所示,以为坐标原点,,,所在的直线分别为,,轴,建立空间直角坐标系.
知识应用
所以,,,
所以.
又因为平面,所以平面.
(2) 由(1)可知,,.
设平面的法向量为,
则即
知识应用
令,得,,
则.
设平面的法向量为,
则即
令,得,,则.
所以, 所以平面平面.
知识应用
1.某校积极开展社团活动,在一次社团活动过程中,一个数学兴趣小组发现《九章算术》中提到了“刍甍”这个五面体,于是他们仿照该模型设计了一道数学探究题,如图1,E、F、G分别是正方形的三边AB、CD、AD的中点,先沿着虚线段FG将等腰直角三角形FDG裁掉,再将剩下的五边形ABCFG沿着线段EF折起,连接AB、CG就得到了一个“刍甍”(如图2).
(1)若O是四边形EBCF对角线的交点,
求证:AO//平面GCF;
(2)若二面角A-EF-B是直二面角,求点B到平面GCF的距离.
3.空间向量解决距离问题
知识应用
(1)证明:取线段CF中点H,连接OH、GH,由图1可知,四边形EBCF是矩形,且CB=2EB,
∴O是线段BF与CE的中点,∴ OH//BC且OH=,在图1中知AG//BC且AG=BC,EF//BC且EF=BC,
所以在图2中,AG//BC且AG=BC,AG//OH且AG=OH,∴四边形AOHG是平行四边形,则AO//HG,
由于AO 平面GCF,HG平面GCF,∴AO//平面GCF.
知识应用
(2)解:由图1,EF,EF折起后在图2中仍有 EF,EF,
∴即为二面角A-EF-E 的平面角,∴=,
以E为坐标原点,分别为 轴和 轴正向建立空间直角坐标系E-xyz,
则B(2,0,0)、C(4,2,0)、F(0,4,0)、A(0,0,2)、G(0,2,2),
∴,
设平面GCF 的一个法向量为
由,得,取,则z=1,
于是平面GCF的一个法向量 =(0,1,1)
点B到平面GCF的距离为d==.
知识应用
4.空间向量解决夹角问题
1.如图,四边形ABCD为菱形,∠ABC=120°,E,F是平面ABCD同一侧的两点,BE⊥平面ABCD,DF⊥平面ABCD,BE=2DF,AE⊥EC.
(1)证明:平面AEC⊥平面AFC;
(2)求直线AE与直线CF所成角的余弦值.
知识应用
知识应用
知识应用
2.如图,在正三棱柱ABC-A1B1C1中,2AB=AA1=4,CE=EC1,AF=3FA1.
(1)证明:BE 平面B1EF;
(2)求面EBF与面BFA夹角的余弦值.
解:(1)由条件可知BE=,BF=,EF=,
满足 ,EF BE.
BE=B1E=,BB1=4,
满足,BE B1E.
又 B1E, BE平面B1EF.
知识应用
(2)以AC 的中点O为坐标原点,建立如图所示的空间直角坐标系 O- xyz,
则B(0,,E(-1,0,2),F (1,0,3). ,,
设平面 BEF 的法向量为,,
取 得 = (.
易得平面 ABF 的一个法向量为 ,
cos,
面EBF与面BFA夹角的余弦值.
例3 如图,已知三棱柱ABC-A1B1C1的侧棱与底面垂直,AA1=AB=AC=1,AB⊥AC,M,N分别是CC1,BC的中点,点P在直线A1B1上,且A1P=λA1B1.
(1)证明:无论λ取何值,总有AM⊥PN;
(2)是否存在点P,使得平面PMN与平面ABC所成的角为30°?若存在,试确定点P的位置;若不存在,请说明理由.
知识应用
5.空间向量探索性问题
1.如图,已知三棱柱ABC-A1B1C1的侧棱与底面垂直,AA1=AB=AC=1,AB⊥AC,M,N分别是CC1,BC的中点,点P在直线A1B1上,且A1P=λA1B1.
(1)证明:无论λ取何值,总有AM⊥PN;
(2)是否存在点P,使得平面PMN与平面ABC所成的角为30°?若存在,试确定点P的位置;若不存在,请说明理由.
知识应用
知识应用
