湖南省常德市名校2023-2024学年高二上学期入学考试数学试题(PDF版含答案)
文档属性
| 名称 | 湖南省常德市名校2023-2024学年高二上学期入学考试数学试题(PDF版含答案) |

|
|
| 格式 | |||
| 文件大小 | 346.4KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教A版(2019) | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-09-12 00:00:00 | ||
图片预览


文档简介
常德市名校 2023年下学期高二年级入学考试试卷
数 学
时量:120 分钟 满分:150 分
一、单选题:本题共 8小题,每小题 5分,共 40分.在每小题给出的四个选项中,只有一项是符合
题目要求的.
1 2.已知集合 P x x 2x 0 ,Q x log2 x 1 1 ,则 RP Q
A. 0,1 B. 0,2 C. 1, 2 D. 1,2
2.如果不等式 x a 1
1 3
成立的充分非必要条件是 x ,则实数 a的取值范围是
2 2
1 3 1 3 3 1 3 1
A. a B. a C. a 或 a D. a 或 a
2 2 2 2 7 2 2 2
3π
3.已知扇形面积 ,半径是 1,则扇形的周长是
8
3π 1 3π 3πA. B. 2 C. 2
3π
D. 1
16 8 4 2
1
4 .设 a,b 为单位向量, a在b 方向上的投影向量为 b,则 a 2b 2
A. 2 B. 3 C. 5 D. 7
5.已知0 m 1,0 n 1,且 2log4m log2 1 n
1 9
,则 的最小值是
m n
A.18 B.16 C.10 D.4
6 a 20.5.下列三个数: ,b 0.32 , c log2 3,大小顺序正确的是
A. a b c B. a c b C. c a b D.b a c
7.如图,二面角 l 等于120 , A,B是棱 l上两点, BD,AC分别在半平面 , 内,
AC l , BD l,且 AB AC BD 2,则CD的长等于
A.2 3 B.2 2 C.4 D.2
8.已知函数 f x 2cos π x ( 0),若 f x 在区间 0,π 内有且仅有 3 个零点和 3 条对称轴,则 的取值范
6
围是
17 ,10 17A. B. ,
23 17 ,10 7 10 C.
6 3 6 6 6 3
D. ,
3 3
1
{#{QQABCYQQggCgAAIAARhCUQHSCEOQkAECAIgOgAAMoAAByAFABAA=}#}
二、多选题:本题共 4小题,每小题 5分,共 20分.在每小题给出的选项中,有多项符合题目要求.
全部选对的得 5分,部分选对的得 2分,有选错的得 0分.
9.下列各式中值为 1 的是
A 2sin15 cos15 B cos275 sin 275 C 3. . . 2sin215 D.sin2 2023 cos2 2023
2
10.若 P AB 1 , P A 2 ,P B 1 ,则事件A 与 B的关系错误是
9 3 3
A.事件A 与 B互斥 B.事件A 与 B对立
C.事件A 与 B相互独立 D.事件A 与 B既互斥又独立
π
11.已知函数 f x Asin x , A 0, 0, 2 部分图象如图所示,下列说法正确的是
5π
A. f x 的图象关于直线 x 对称
12
f x 2π B. 的图象关于点 ,0 中心对称
3
π
C.将函数 y 3 sin 2x cos 2x的图象向左平移 个单位得到函数 f x 的图象
2
D.若方程 f x π m 在 ,0 上有两个不相等的实数根,则m的取值范围是 2, 3 2
12.如图,已知正方体 ABCD A1B1C1D1的棱长为 1,O为底面 ABCD的中心,
AC1交平面 A1BD于点 E,点 F为棱 CD的中点,则
A. A1,E,O三点共线 B.异面直线 BD与 AC1所成的角为90
8
C 3.点C1到平面 A1BD的距离为 D.过点 A1,B,F的平面截该正方体所得截面的面积为3 9
三、填空题(本题共 4小题,每小题 5分,共 20分)
13 .已知平面向量 a sin ,1 ,b 2,cos ,若 a b,则 tan .
14 4a 3b 6 2a b.已知 ,则 .
ab
15.正三棱锥 P ABC底面边长为 2,M为 AB的中点,且PM PC,则正三棱锥 P ABC外接球的体积为 .
16.在 ABC中, ACB 60 ,BC 2, AC AB 1,则 ABC周长的最小值为 .
四、解答题(共 70分,17题 10分,18-22题每题 12分)
1
17. (本小题满分 10 分)在 ABC中,A,B,C的对边分别为 a,b,c,若满足 c 3, cos B .
3
(1)若 a 1,求b的大小;
(2)若满足 S a ABC 2 2 ,求 及 sin A 的值.
2
{#{QQABCYQQggCgAAIAARhCUQHSCEOQkAECAIgOgAAMoAAByAFABAA=}#}
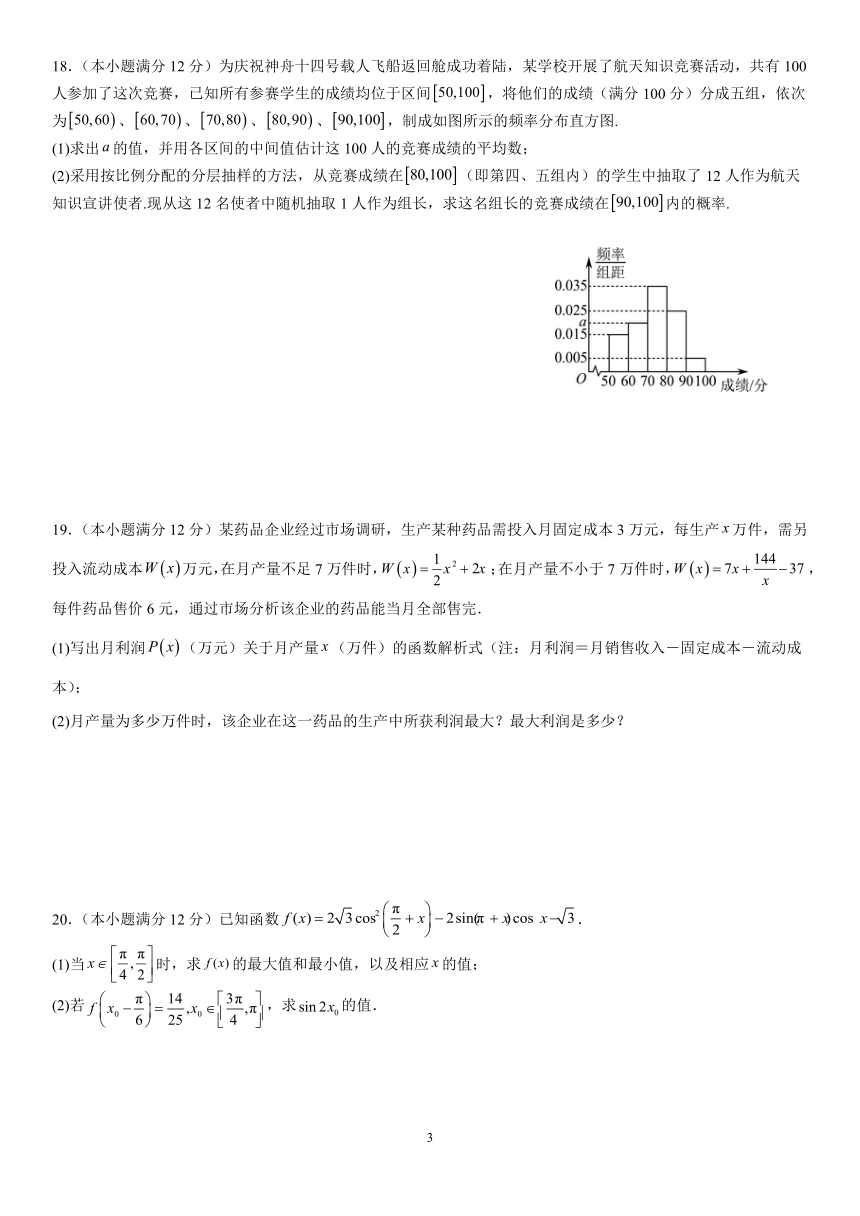
18.(本小题满分 12 分)为庆祝神舟十四号载人飞船返回舱成功着陆,某学校开展了航天知识竞赛活动,共有 100
人参加了这次竞赛,已知所有参赛学生的成绩均位于区间 50,100 ,将他们的成绩(满分 100 分)分成五组,依次
为 50,60 、 60,70 、 70,80 、 80,90 、 90,100 ,制成如图所示的频率分布直方图.
(1)求出 a的值,并用各区间的中间值估计这 100 人的竞赛成绩的平均数;
(2)采用按比例分配的分层抽样的方法,从竞赛成绩在 80,100 (即第四、五组内)的学生中抽取了 12 人作为航天
知识宣讲使者.现从这 12 名使者中随机抽取 1 人作为组长,求这名组长的竞赛成绩在 90,100 内的概率.
19.(本小题满分 12 分)某药品企业经过市场调研,生产某种药品需投入月固定成本 3 万元,每生产 x万件,需另
投入流动成本W x 1 2 144万元,在月产量不足 7 万件时,W x x 2x ;在月产量不小于 7 万件时,W x 7x 37 ,
2 x
每件药品售价 6 元,通过市场分析该企业的药品能当月全部售完.
(1)写出月利润P x (万元)关于月产量 x(万件)的函数解析式(注:月利润=月销售收入-固定成本-流动成
本);
(2)月产量为多少万件时,该企业在这一药品的生产中所获利润最大?最大利润是多少?
π
20 2.(本小题满分 12 分)已知函数 f (x) 2 3 cos x 2sin(π x) cos x 3.
2
π π
(1)当 x , 时,求 f (x) 的最大值和最小值,以及相应 x的值; 4 2
(2)若 f x π 14 3π ,求 的值.0 ,x ,π sin 2x
6 25 0
0
4
3
{#{QQABCYQQggCgAAIAARhCUQHSCEOQkAECAIgOgAAMoAAByAFABAA=}#}
21. (本小题满分 12 分)如图,在三棱锥 A BCD中,平面 ABD 平面 BCD, AB AD,O为 BD的中点.
(1)证明:OA CD;
(2)若 OCD是边长为 1的等边三角形,点 E在棱 AD上,DE 2EA,且二面角 E BC D的大小为 45 ,
求三棱锥 A BCD的体积.
x x 1
22 2 b.(本小题满分 12 分)已知函数 f x , g x logx a ( a 0且a 1),且 f 0 0 .2 b x b
(1)求 b的值,判断函数 g x 的奇偶性并说明理由;
(2)当a 2时,求不等式 g x 1的解集;
(3)若关于 x的方程m f x
2
m 1 f x 3 0有两个不同的解,求实数 m的取值范围.
4
{#{QQABCYQQggCgAAIAARhCUQHSCEOQkAECAIgOgAAMoAAByAFABAA=}#}
常德市名校 2023年下学期高二年级入学考试数学参考答案
一单选题:(40 分)
1.C 2.B 3.C 4.D 5.B 6.C 7.C 8.A
二.多选题:(20 分)
9.CD 10.ABD 11.AD 12.AB
三填空题:(20 分)
1
13. 14.2 15. 6π 16.9 6 2
2
四.解答题:
17.解:(1)若 a 1,由余弦定理b2 a2 c2 2ac cosB ,
2
可得b 1 9 2 1 3 1 8,即b 2 2 ................................................................... 4 分3
1 2 2
(2)因为 cos B 0 ,可知角 B为锐角,则 sin B 1 cos 2 B ,
3 3
1
又因为 S ABC ac sin B
1 a 3 2 2,即2 2 2
,解得a 2,................................. 7 分
2 3
b2 a2 c2由余弦定理 2accosB 4 9 2 2 3 1 9,即b 3 ,
3
b a 2 2 2
由正弦定理 ,可得 a sin B 3 4 2 . .................................10 分sin B sin A sin A
b 3 9
18.解(1)由 0.015 a 0.035 0.025 0.005 10 1,解得a 0.02;
这 100 人的竞赛成绩的平均数估计为:55 0.15 65 0.2 75 0.35 85 0.25 95 0.05 73.5 ...................4 分
(2)成绩在 80,90 的频率为 0.25,成绩在 90,100 的频率为 0.05,...............6 分
所以竞赛成绩在 80,90 , 90,100 两个组的人数之比为5:1,采用分层抽样的方法从中抽取12人,
所以成绩在 80,90 5 1抽得的人数为12 10人,成绩在 90,100 抽得的人数为12 2 人
6 6
2 1
现从这 12 名使者中随机抽取 1 人作为组长,则这名组长的竞赛成绩在 90,100 内的概率为 ...............12 分
12 6
1 1
19.解:(1 2)由题意得,当0 x 7时, P x 6x x 2x 3 x 2 4x 3 , ...........3 分
2 2
P x 6x 144 144当 x 7时, 7x 37 3 34 x ,
x x
5
{#{QQABCYQQggCgAAIAARhCUQHSCEOQkAECAIgOgAAMoAAByAFABAA=}#}
1 x2 4x 3,0 x 7
P x 2故 144 ..............6 分 34 x , x 7
x
1
(2)当0 x 7时, P x x 4 2 5,当 x 4时, P x 最大值为 5 万元..............8 分
2
当 x 7时, P x 34 x 144 34 2 x
144
10, .............10 分
x x
144
当且仅当 x ,即 x 12时等号成立,即P x 最大值为 10 万元.
x
∵5 10 ,∴当月产量为 12 万件时,该企业所获利润最大值为 10 万元. .............12 分
π π π π 2π
20.解:(1) x , t 2x , ,
4 2 3 6 3
t π π π 1当 即 x 时, sin t sin y
6 4 min
,此时
6 2 min
1, . ............3 分
t π π当 x
5π
即 时, sin t sin 112 max 此时 ymax 2. .............6 分2 2
π
(2) f x0 2sin
2 x
π π
0 2sin
2π 14
6 6 3
2x0 , ............8 分
3 25
sin 2x 2π 7 , 3π 5π 2π 4π 0 x0 π, 2x0 ,
3 25 4 6 3 3
cos 2x
2π
0
1 sin
2
2x
2π 24
0 , ............8 分
3 3 25
2π 2π 2π ............12 分sin2x sin 2x sin 2x 2π 2π 2π0 0
3 3
0 3
cos cos 2x
3 0
3
sin
3
7 1 24 3 24 3 7
25 2 25 2 50
21.解:(1)因为 AB=AD,O 为 BD 中点,所以 AO⊥BD
因为平面 ABD 平面 BCD=BD ,平面 ABD⊥平面 BCD, AO 平面 ABD,
因此 AO⊥平面 BCD,因为CD 平面 BCD,所以 AO⊥CD.. ..........5 分
(2)作 EF⊥BD 于 F, 作 FM⊥BC 于 M,连 FM,因为 AO⊥平面 BCD,所以 AO⊥BD, AO⊥CD
所以 EF⊥BD, EF⊥CD, BD CD D ,因此 EF⊥平面 BCD,即 EF⊥BC,
因为 FM⊥BC, FM I EF F ,所以 BC⊥平面 EFM,即 BC⊥MF,
EMF 则 EMF 为二面角 E-BC-D 的平面角, ,..........8 分
4
因为 BO OD , OCD为正三角形,所以 OCD为直角三角形,
6
{#{QQABCYQQggCgAAIAARhCUQHSCEOQkAECAIgOgAAMoAAByAFABAA=}#}
1 1
因为 BE 2ED , FM BF (1
1) 2
2 2 3 3
2
AO 1 Q AO V 1 1 1 3从而 EF=FM= 平面 BCD,所以3 AO S BCD 1 1 3
..........12 分
3 3 2 6
1 b x
22.解:(1)由 f 0 0 2 1 g x log x 1得b 1,故 f x , .1 b 2x 1 a x 1
g x 为奇函数,理由如下:
g x x 1定义域满足 0,即 x , 1 1, ,
x 1
g x log x 1 log x 1
1 x 1
又 a
x 1 a
loga g x ,故 g x 为奇函数...........3 分
x 1 x 1
x 1 x 1 x 3
(2) a 2, g x log2 1 log 2 2 ,即 2,即 0,解得 x 3, 1 .x 1 x 1 x 1
故不等式 g x 1的解集为 3, 1 . ..........6 分
3 2
x 1 2 2
( ) f x 的定义域为R, f x x 1 x ,为增函数,∵ 2x 1 1,∴0 x 2 ,∴ f x 1,1 .2 1 2 1 2 1
f x 3
经检验 f 0 0 2
不符合方程m f x m 1 f x 3 0,故可化为m f 2 x f x ,
1 f
2 x ff x 1,1 x 又 ,可化为 ,令 t = - f (x)+ 3 (2,3) (3,4 ),则m f x 3
3 t 21 t 3 t2 5t 6 t 6 5 .
m t t t
∵关于 x的方程m f
2
x m 1 f x
1 6
3 0有两个不同的解,即等价于 t 5在 t
m t (2,3) (3,4)有两个不
1
同的解,即等价于 y 与 g t t 6 5的图象在 t (2,3) (3, 4)有两个交点.m t
6 6
∵ g t t 5 2 t 5 2 6 5,当且仅当 t 6 时等号成立,且 g t 在 2, 6 单调递减,在( 6,3)、(3,4)单t t
调递增, g(2) = g(3),
1 6 1
故当 y 与 g t t 5的图象在 t (2,3) (3, 4)有两个交点时, (2 6 - 5,0),即m (- ,-2 6 - 5 .m t m )
故实数 m的取值范围为(- ,-2 6 - 5) . ..........12 分
7
{#{QQABCYQQggCgAAIAARhCUQHSCEOQkAECAIgOgAAMoAAByAFABAA=}#}
数 学
时量:120 分钟 满分:150 分
一、单选题:本题共 8小题,每小题 5分,共 40分.在每小题给出的四个选项中,只有一项是符合
题目要求的.
1 2.已知集合 P x x 2x 0 ,Q x log2 x 1 1 ,则 RP Q
A. 0,1 B. 0,2 C. 1, 2 D. 1,2
2.如果不等式 x a 1
1 3
成立的充分非必要条件是 x ,则实数 a的取值范围是
2 2
1 3 1 3 3 1 3 1
A. a B. a C. a 或 a D. a 或 a
2 2 2 2 7 2 2 2
3π
3.已知扇形面积 ,半径是 1,则扇形的周长是
8
3π 1 3π 3πA. B. 2 C. 2
3π
D. 1
16 8 4 2
1
4 .设 a,b 为单位向量, a在b 方向上的投影向量为 b,则 a 2b 2
A. 2 B. 3 C. 5 D. 7
5.已知0 m 1,0 n 1,且 2log4m log2 1 n
1 9
,则 的最小值是
m n
A.18 B.16 C.10 D.4
6 a 20.5.下列三个数: ,b 0.32 , c log2 3,大小顺序正确的是
A. a b c B. a c b C. c a b D.b a c
7.如图,二面角 l 等于120 , A,B是棱 l上两点, BD,AC分别在半平面 , 内,
AC l , BD l,且 AB AC BD 2,则CD的长等于
A.2 3 B.2 2 C.4 D.2
8.已知函数 f x 2cos π x ( 0),若 f x 在区间 0,π 内有且仅有 3 个零点和 3 条对称轴,则 的取值范
6
围是
17 ,10 17A. B. ,
23 17 ,10 7 10 C.
6 3 6 6 6 3
D. ,
3 3
1
{#{QQABCYQQggCgAAIAARhCUQHSCEOQkAECAIgOgAAMoAAByAFABAA=}#}
二、多选题:本题共 4小题,每小题 5分,共 20分.在每小题给出的选项中,有多项符合题目要求.
全部选对的得 5分,部分选对的得 2分,有选错的得 0分.
9.下列各式中值为 1 的是
A 2sin15 cos15 B cos275 sin 275 C 3. . . 2sin215 D.sin2 2023 cos2 2023
2
10.若 P AB 1 , P A 2 ,P B 1 ,则事件A 与 B的关系错误是
9 3 3
A.事件A 与 B互斥 B.事件A 与 B对立
C.事件A 与 B相互独立 D.事件A 与 B既互斥又独立
π
11.已知函数 f x Asin x , A 0, 0, 2 部分图象如图所示,下列说法正确的是
5π
A. f x 的图象关于直线 x 对称
12
f x 2π B. 的图象关于点 ,0 中心对称
3
π
C.将函数 y 3 sin 2x cos 2x的图象向左平移 个单位得到函数 f x 的图象
2
D.若方程 f x π m 在 ,0 上有两个不相等的实数根,则m的取值范围是 2, 3 2
12.如图,已知正方体 ABCD A1B1C1D1的棱长为 1,O为底面 ABCD的中心,
AC1交平面 A1BD于点 E,点 F为棱 CD的中点,则
A. A1,E,O三点共线 B.异面直线 BD与 AC1所成的角为90
8
C 3.点C1到平面 A1BD的距离为 D.过点 A1,B,F的平面截该正方体所得截面的面积为3 9
三、填空题(本题共 4小题,每小题 5分,共 20分)
13 .已知平面向量 a sin ,1 ,b 2,cos ,若 a b,则 tan .
14 4a 3b 6 2a b.已知 ,则 .
ab
15.正三棱锥 P ABC底面边长为 2,M为 AB的中点,且PM PC,则正三棱锥 P ABC外接球的体积为 .
16.在 ABC中, ACB 60 ,BC 2, AC AB 1,则 ABC周长的最小值为 .
四、解答题(共 70分,17题 10分,18-22题每题 12分)
1
17. (本小题满分 10 分)在 ABC中,A,B,C的对边分别为 a,b,c,若满足 c 3, cos B .
3
(1)若 a 1,求b的大小;
(2)若满足 S a ABC 2 2 ,求 及 sin A 的值.
2
{#{QQABCYQQggCgAAIAARhCUQHSCEOQkAECAIgOgAAMoAAByAFABAA=}#}
18.(本小题满分 12 分)为庆祝神舟十四号载人飞船返回舱成功着陆,某学校开展了航天知识竞赛活动,共有 100
人参加了这次竞赛,已知所有参赛学生的成绩均位于区间 50,100 ,将他们的成绩(满分 100 分)分成五组,依次
为 50,60 、 60,70 、 70,80 、 80,90 、 90,100 ,制成如图所示的频率分布直方图.
(1)求出 a的值,并用各区间的中间值估计这 100 人的竞赛成绩的平均数;
(2)采用按比例分配的分层抽样的方法,从竞赛成绩在 80,100 (即第四、五组内)的学生中抽取了 12 人作为航天
知识宣讲使者.现从这 12 名使者中随机抽取 1 人作为组长,求这名组长的竞赛成绩在 90,100 内的概率.
19.(本小题满分 12 分)某药品企业经过市场调研,生产某种药品需投入月固定成本 3 万元,每生产 x万件,需另
投入流动成本W x 1 2 144万元,在月产量不足 7 万件时,W x x 2x ;在月产量不小于 7 万件时,W x 7x 37 ,
2 x
每件药品售价 6 元,通过市场分析该企业的药品能当月全部售完.
(1)写出月利润P x (万元)关于月产量 x(万件)的函数解析式(注:月利润=月销售收入-固定成本-流动成
本);
(2)月产量为多少万件时,该企业在这一药品的生产中所获利润最大?最大利润是多少?
π
20 2.(本小题满分 12 分)已知函数 f (x) 2 3 cos x 2sin(π x) cos x 3.
2
π π
(1)当 x , 时,求 f (x) 的最大值和最小值,以及相应 x的值; 4 2
(2)若 f x π 14 3π ,求 的值.0 ,x ,π sin 2x
6 25 0
0
4
3
{#{QQABCYQQggCgAAIAARhCUQHSCEOQkAECAIgOgAAMoAAByAFABAA=}#}
21. (本小题满分 12 分)如图,在三棱锥 A BCD中,平面 ABD 平面 BCD, AB AD,O为 BD的中点.
(1)证明:OA CD;
(2)若 OCD是边长为 1的等边三角形,点 E在棱 AD上,DE 2EA,且二面角 E BC D的大小为 45 ,
求三棱锥 A BCD的体积.
x x 1
22 2 b.(本小题满分 12 分)已知函数 f x , g x logx a ( a 0且a 1),且 f 0 0 .2 b x b
(1)求 b的值,判断函数 g x 的奇偶性并说明理由;
(2)当a 2时,求不等式 g x 1的解集;
(3)若关于 x的方程m f x
2
m 1 f x 3 0有两个不同的解,求实数 m的取值范围.
4
{#{QQABCYQQggCgAAIAARhCUQHSCEOQkAECAIgOgAAMoAAByAFABAA=}#}
常德市名校 2023年下学期高二年级入学考试数学参考答案
一单选题:(40 分)
1.C 2.B 3.C 4.D 5.B 6.C 7.C 8.A
二.多选题:(20 分)
9.CD 10.ABD 11.AD 12.AB
三填空题:(20 分)
1
13. 14.2 15. 6π 16.9 6 2
2
四.解答题:
17.解:(1)若 a 1,由余弦定理b2 a2 c2 2ac cosB ,
2
可得b 1 9 2 1 3 1 8,即b 2 2 ................................................................... 4 分3
1 2 2
(2)因为 cos B 0 ,可知角 B为锐角,则 sin B 1 cos 2 B ,
3 3
1
又因为 S ABC ac sin B
1 a 3 2 2,即2 2 2
,解得a 2,................................. 7 分
2 3
b2 a2 c2由余弦定理 2accosB 4 9 2 2 3 1 9,即b 3 ,
3
b a 2 2 2
由正弦定理 ,可得 a sin B 3 4 2 . .................................10 分sin B sin A sin A
b 3 9
18.解(1)由 0.015 a 0.035 0.025 0.005 10 1,解得a 0.02;
这 100 人的竞赛成绩的平均数估计为:55 0.15 65 0.2 75 0.35 85 0.25 95 0.05 73.5 ...................4 分
(2)成绩在 80,90 的频率为 0.25,成绩在 90,100 的频率为 0.05,...............6 分
所以竞赛成绩在 80,90 , 90,100 两个组的人数之比为5:1,采用分层抽样的方法从中抽取12人,
所以成绩在 80,90 5 1抽得的人数为12 10人,成绩在 90,100 抽得的人数为12 2 人
6 6
2 1
现从这 12 名使者中随机抽取 1 人作为组长,则这名组长的竞赛成绩在 90,100 内的概率为 ...............12 分
12 6
1 1
19.解:(1 2)由题意得,当0 x 7时, P x 6x x 2x 3 x 2 4x 3 , ...........3 分
2 2
P x 6x 144 144当 x 7时, 7x 37 3 34 x ,
x x
5
{#{QQABCYQQggCgAAIAARhCUQHSCEOQkAECAIgOgAAMoAAByAFABAA=}#}
1 x2 4x 3,0 x 7
P x 2故 144 ..............6 分 34 x , x 7
x
1
(2)当0 x 7时, P x x 4 2 5,当 x 4时, P x 最大值为 5 万元..............8 分
2
当 x 7时, P x 34 x 144 34 2 x
144
10, .............10 分
x x
144
当且仅当 x ,即 x 12时等号成立,即P x 最大值为 10 万元.
x
∵5 10 ,∴当月产量为 12 万件时,该企业所获利润最大值为 10 万元. .............12 分
π π π π 2π
20.解:(1) x , t 2x , ,
4 2 3 6 3
t π π π 1当 即 x 时, sin t sin y
6 4 min
,此时
6 2 min
1, . ............3 分
t π π当 x
5π
即 时, sin t sin 112 max 此时 ymax 2. .............6 分2 2
π
(2) f x0 2sin
2 x
π π
0 2sin
2π 14
6 6 3
2x0 , ............8 分
3 25
sin 2x 2π 7 , 3π 5π 2π 4π 0 x0 π, 2x0 ,
3 25 4 6 3 3
cos 2x
2π
0
1 sin
2
2x
2π 24
0 , ............8 分
3 3 25
2π 2π 2π ............12 分sin2x sin 2x sin 2x 2π 2π 2π0 0
3 3
0 3
cos cos 2x
3 0
3
sin
3
7 1 24 3 24 3 7
25 2 25 2 50
21.解:(1)因为 AB=AD,O 为 BD 中点,所以 AO⊥BD
因为平面 ABD 平面 BCD=BD ,平面 ABD⊥平面 BCD, AO 平面 ABD,
因此 AO⊥平面 BCD,因为CD 平面 BCD,所以 AO⊥CD.. ..........5 分
(2)作 EF⊥BD 于 F, 作 FM⊥BC 于 M,连 FM,因为 AO⊥平面 BCD,所以 AO⊥BD, AO⊥CD
所以 EF⊥BD, EF⊥CD, BD CD D ,因此 EF⊥平面 BCD,即 EF⊥BC,
因为 FM⊥BC, FM I EF F ,所以 BC⊥平面 EFM,即 BC⊥MF,
EMF 则 EMF 为二面角 E-BC-D 的平面角, ,..........8 分
4
因为 BO OD , OCD为正三角形,所以 OCD为直角三角形,
6
{#{QQABCYQQggCgAAIAARhCUQHSCEOQkAECAIgOgAAMoAAByAFABAA=}#}
1 1
因为 BE 2ED , FM BF (1
1) 2
2 2 3 3
2
AO 1 Q AO V 1 1 1 3从而 EF=FM= 平面 BCD,所以3 AO S BCD 1 1 3
..........12 分
3 3 2 6
1 b x
22.解:(1)由 f 0 0 2 1 g x log x 1得b 1,故 f x , .1 b 2x 1 a x 1
g x 为奇函数,理由如下:
g x x 1定义域满足 0,即 x , 1 1, ,
x 1
g x log x 1 log x 1
1 x 1
又 a
x 1 a
loga g x ,故 g x 为奇函数...........3 分
x 1 x 1
x 1 x 1 x 3
(2) a 2, g x log2 1 log 2 2 ,即 2,即 0,解得 x 3, 1 .x 1 x 1 x 1
故不等式 g x 1的解集为 3, 1 . ..........6 分
3 2
x 1 2 2
( ) f x 的定义域为R, f x x 1 x ,为增函数,∵ 2x 1 1,∴0 x 2 ,∴ f x 1,1 .2 1 2 1 2 1
f x 3
经检验 f 0 0 2
不符合方程m f x m 1 f x 3 0,故可化为m f 2 x f x ,
1 f
2 x ff x 1,1 x 又 ,可化为 ,令 t = - f (x)+ 3 (2,3) (3,4 ),则m f x 3
3 t 21 t 3 t2 5t 6 t 6 5 .
m t t t
∵关于 x的方程m f
2
x m 1 f x
1 6
3 0有两个不同的解,即等价于 t 5在 t
m t (2,3) (3,4)有两个不
1
同的解,即等价于 y 与 g t t 6 5的图象在 t (2,3) (3, 4)有两个交点.m t
6 6
∵ g t t 5 2 t 5 2 6 5,当且仅当 t 6 时等号成立,且 g t 在 2, 6 单调递减,在( 6,3)、(3,4)单t t
调递增, g(2) = g(3),
1 6 1
故当 y 与 g t t 5的图象在 t (2,3) (3, 4)有两个交点时, (2 6 - 5,0),即m (- ,-2 6 - 5 .m t m )
故实数 m的取值范围为(- ,-2 6 - 5) . ..........12 分
7
{#{QQABCYQQggCgAAIAARhCUQHSCEOQkAECAIgOgAAMoAAByAFABAA=}#}
同课章节目录
